Dans la première partie, nous avons examiné l'algèbre externe et réalisé que les vecteurs normaux en 3D peuvent être interprétés comme des bivecteurs. Pour transformer des bivecteurs, dans le cas général, vous avez besoin d'une matrice différente de celle qui transforme les vecteurs ordinaires. En utilisant la base canonique des bivecteurs, nous avons découvert qu'il s'agit de la matrice adjointe , qui est proportionnelle à la transposée inverse. Ce raisonnement explique au moins en partie pourquoi les normales sont transformées par la matrice transposée inverse.
Mais certains problèmes ont été balayés sous le tapis.
Nous avons considéré les matrices adjointe, mais n'avons pas montré comment elles se rapportent à la preuve algébrique que pour transformer l'équation planeune matrice transposée inverse est nécessaire. La proportionnalité entre les matrices était, en un sens, exagérée.
De plus, nous avons vu que -les vecteurs d'algèbre externe fournissent aux objets géométriques vectoriels une interprétation naturelle, dans laquelle ils contiennent des unités de longueur, de surface et de volume, qui changent en conséquence lorsqu'ils sont mis à l'échelle. Mais nous n'avons rien trouvé de tel pour les densités - unités inverses de la longueur, de la surface et du volume.
Dans cet article, nous examinerons un autre concept géométrique qui sera nécessaire pour compléter la peinture. La fusion de ce nouveau concept avec l'algèbre externe déjà étudiée clarifiera et résoudra les questions restantes.
Fonctions comme vecteurs
, . , , , .
: , ,
. — , … , ? ?
, . , (). , , : ( ). .
! . , : . , , .
: ( , ) — . . , , "". .
. , .
, .
, , . , .
( : , . !)
(3D) (2D), / , . :
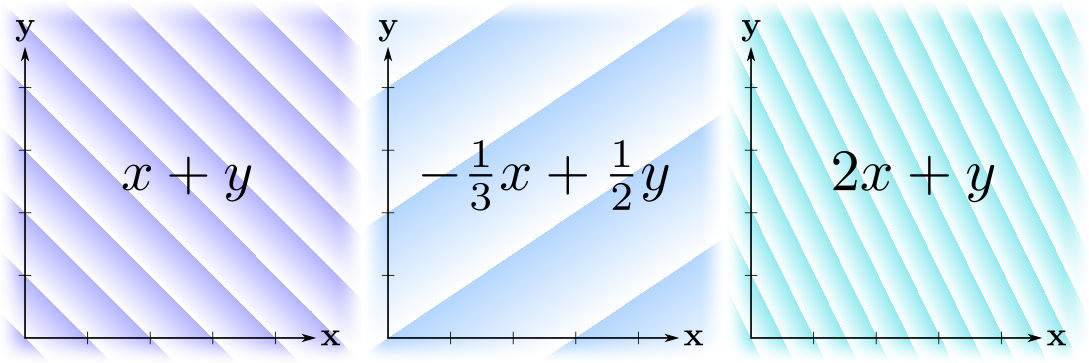
— . . , "́" ( ́ ) , .
, . , .
— — , : ( ) . . ( ) .
, — , , . - , , . , , .
, . . , — — , :
, — !
, : . .
, , , . , , "" . , — , … .
: . — , — . , . , — , .
:
, " " , .
. , , . :
. :
.
, , , . , . , . .
:
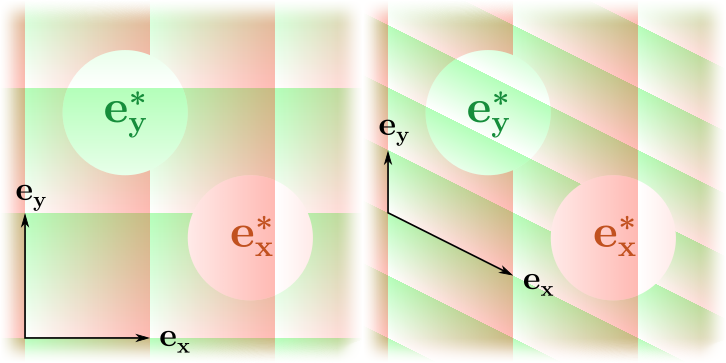
:
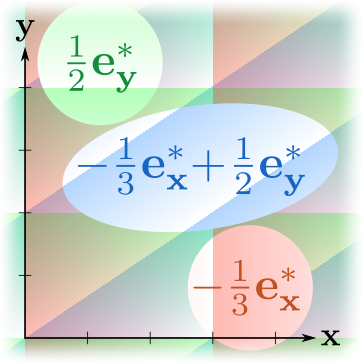
. :
, ( ), , , .
! "" ( ), ( 3D), ( ). !
— , . ?
: . , . : - . ( , ).
: , , . :
, , .
, . " " : .
, , . , . .
, . , ?
, , . , :
! , . "" "" . , , !
, . , (, , , //) - . ( ), " "" ?"
"". , , - , . .
. , , — , . .
. , :
:

? : .
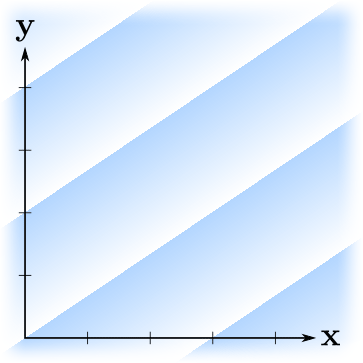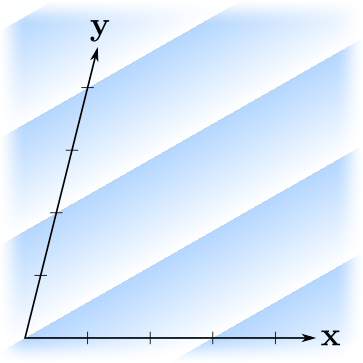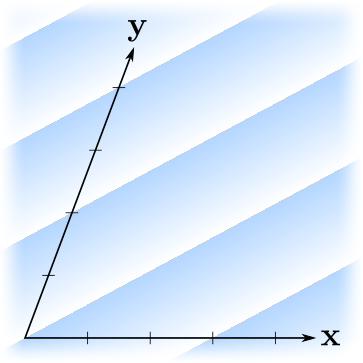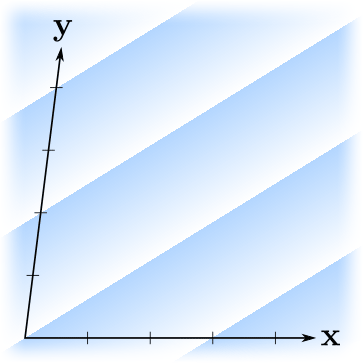
, ? . , — . ?
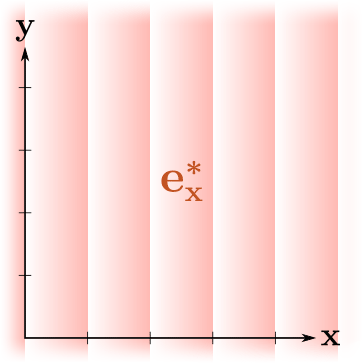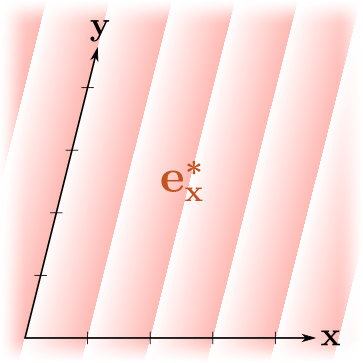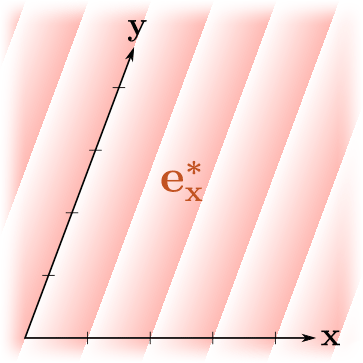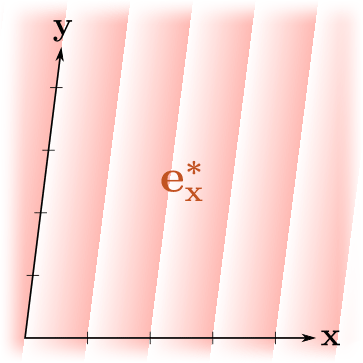
, ! , , , "" , . , .
, . , , , ,
!
, , . , , ( ), . :
.
, , .
?
, — 2D 3D. , , :
.
, , . :
, .
, , .
. , , , ? ?
, . " " , , . , : , . : , — .
C'est tout ce que je voulais dire sur les transformations des vecteurs normaux, mais quelques autres questions restaient dans les limbes. À la fin de la première partie, j'ai posé une question sur les degrés d'échelle négatifs. Maintenant, nous avons moins le premier degré, mais qu'en est-il de -2 et -3? Pour comprendre cela, nous devons combiner algèbre externe et espaces duels, ce que nous ferons dans la troisième partie.