NaN peut encore vous surprendre un peu

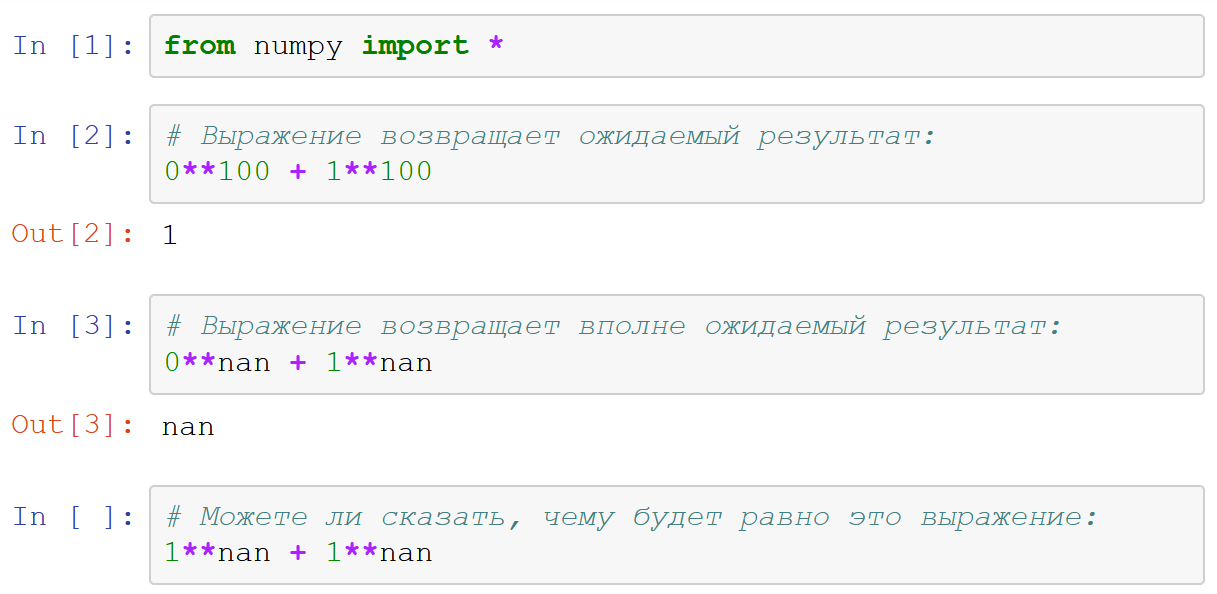
Au début, je pensais que c'était juste une autre question qui pourrait être posée lors d'une interview. Probablement, si vous utilisez correctement votre cerveau, vous pouvez deviner quel sera le résultat. Se penchant en arrière sur sa chaise, il commença à réfléchir, à activer la logique, à se souvenir de quelque chose sur lequel s'appuyer pour raisonner. Mais en vain! Soudain, il est devenu assez évident que la réponse ne pouvait pas être trouvée. Mais pourquoi? Que devez-vous comprendre pour le trouver? En mathématiques? Dans un langage de programmation?



La réponse devrait être NaN. Mais pourquoi ne suis-je pas sûr de cela? Pendant tout ce temps, j'étais convaincu que toute expression contenant NaN renverrait NaN. Eh bien, peut-être seulement si vous divisez NaN par zéro - dans ce cas, une exception ZeroDivisionError sera levée . Cent pour cent NaN!



J'entre l'expression dans une cellule du bloc-notes:

>>> 1**nan + 1**nan
2.0

En effet? Attendez:

>>> arange(5)**nan
array([nan,  1., nan, nan, nan])

Autrement dit, pour une raison quelconque, un à la puissance NaN est un, mais zéro et tous les autres nombres à la puissance NaN sont NaN. Où est la logique? Quel est le problème?



Alors repartons:

>>> 0**nan, 1**nan
(nan, 1.0)

Peut-être étais-je juste à cause du manque de besoin pratique d'une connaissance approfondie de NaN, je ne soupçonnais tout simplement pas quelque chose? Ou peut-être que je savais, mais j'ai oublié? Ou peut-être même pire - je ne savais pas et j'avais oublié?



Nous allons sur Wikipedia . Là, ce problème est également désigné comme un problème, mais la raison pour laquelle tout est organisé de cette manière n'est en aucun cas expliquée. Mais j'ai appris que:

>>> hypot(inf, nan)
inf

Bien que, en même temps:

>>> sqrt(inf**2 + nan**2)
nan

Cela, vous voyez, est également un peu étrange.



D'accord, de Wikipédia, nous allons à C99 à la page 182 et obtenons enfin une explication logique pourquoi pow (x, 0) renvoie 1 pour tout x , même pour x égal à NaN:

>>> power(nan, 0)
1.0

Si la fonction $$$f(x)$ est élevé au pouvoir $$$g(x)$ et où $$$g(x)$ tend vers 0, alors le résultat sera 1, quelle que soit la valeur $$$f(x)$...







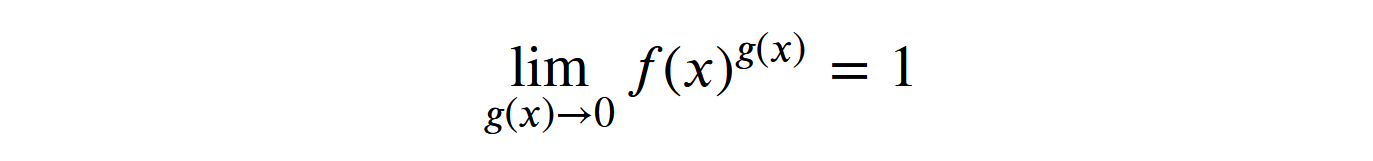
Et si le résultat ne dépend pas de la valeur numérique de la fonction$$$f(x)$, alors 1 est un résultat valide, même pour NaN. Cependant, cela n'explique toujours pas pourquoi 1 à la puissance NaN est 1. Nous



cherchons un autre C99 et à la page 461 nous ne voyons aucune explication, juste l'exigence que pow (+1, y) doit renvoyer 1 pour tout y , même égal NaN. Tout.



D'autre part, expliquer pourquoi pow (NaN, 0) = 1 est préférable à pow (NaN, 0) = NaN suggère toujours que NaN ne doit pas être pris littéralement comme Not-a-Number ... Supposons qu'à la suite de certains calculs, nous obtenions un nombre qui dépasse la taille de la mémoire allouée pour ce type de nombres, par exemple:

>>> a = pi*10e307
>>> a
inf

En conséquence, nous avons obtenu inf , quel est exactement ce nombre que nous ne savons pas, mais c'est quand même une sorte de nombre. Ensuite, nous avons calculé quelque chose encore et encore obtenu un nombre trop grand:

>>> b = e*10e307
>>> b
inf

La différence entre a et b renverra NaN:

>>> c = a - b
>>> c
nan

La seule raison pour laquelle nous pouvons penser que c n'est pas un nombre est que nous n'avons pas utilisé de calculs précis. Cependant, en c, sous NaN, il y a une signification cachée. Nous ne savons pas quelle est cette signification. Mais il s'agit toujours d'un nombre, et puisqu'il s'agit d'un nombre, il n'y a rien d'étonnant à ce que pow (1, NaN) = 1 .



Pourquoi alors pow (0, NaN) = NaN ? Le fait est que si nous élevons 0 à n'importe quelle puissance, alors nous obtenons vraiment zéro. Sauf pour un seul cas - lorsque le degré est 0:

>>> 0**0
1

Pour cette raison, dans l'expression pow (0, NaN), il existe une ambiguïté avec une valeur spécifique de NaN. Bien sûr, la probabilité que 0 puisse être caché sous NaN est extrêmement faible, et on pourrait supposer que pow (0, NaN) = 0 . Mais il vaut toujours mieux jouer la sécurité, on ne sait jamais à quoi cela peut conduire. C'est peut-être ainsi qu'ils ont raisonné lorsque les normes ont été créées.



Je ne sais même pas quoi dire d'autre ... si vous connaissiez la réponse à l'avance, alors vous pouvez très probablement être envié, car les domaines dans lesquels une telle connaissance peut être utile sont probablement remplis de tâches intéressantes. Et peut-être vice versa. Écrivez à ce sujet dans les commentaires.



PS Puisque NaN fait référence à des nombres à virgule flottante, il peut s'agir d'une clé de dictionnaire:

>>> d = {0.1: 'a', nan: 'b'}
>>> d[nan]
'b'

Est-il sensé de l'utiliser dans la pratique? Je ne pense pas que ce soit mieux.