Contrôle des manipulateurs multi-liens d'un complexe robotique à l'aide d'un réseau neuronal

introduction

Lors de la simulation de systèmes de contrôle de mouvement pour robots, il est nécessaire de résoudre les problèmes de cinématique et de dynamique de leurs actionneurs. Il y a un problème inverse et direct de cinématique. Le problème direct de la cinématique est de déterminer la position spatiale et l'orientation du point caractéristique, en règle générale, de l'outil de travail du robot manipulateur par les valeurs connues des coordonnées généralisées. Le problème inverse de la cinématique, comme le problème direct, est l'un des principaux problèmes de l'analyse cinématique et de la synthèse. Pour contrôler la position des liens et l'orientation de l'outil de travail du manipulateur, il devient nécessaire de résoudre le problème inverse de la cinématique.

La plupart des approches analytiques pour résoudre le problème de cinématique inverse sont assez coûteuses en termes de procédures de calcul. L'une des approches alternatives est l'utilisation de réseaux de neurones. Des données d'entrée. Considérez un manipulateur à trois liaisons avec les paramètres indiqués dans le tableau 1.

Tableau 1 - Paramètres DH pour un manipulateur à trois liaisons

Dans l'environnement MatLab, en utilisant la boîte à outils Robotics librement distribuée, un modèle informatique d'un manipulateur à trois liens est construit. Vous trouverez ci-dessous un fragment du script MatLab dans lequel nous attribuons au tableau «L» les valeurs des paramètres, A, Alfa et D du tableau 1. Pour notre modèle, ce sont des valeurs constantes et elles ne changent pas lors du travail avec le manipulateur. Nous affectons le paramètre Tetta à la variable 'initialPose_left' - la position initiale de notre manipulateur. 

function [L,initialPose_left,baseL] =model3z 
%   
initialPose_left = deg2rad([0 0 0]); 
L(1) = Revolute('d', 0.2, 'alpha', pi/2, 'qlim', initialPose_left(1)+deg2rad([-90 +90]) ); 
L(2) = Revolute('d', 0, 'alpha', 0, 'a', 0.4, 'qlim', initialPose_left(2)+deg2rad([-20 +90]));   
L(3) = Revolute('d', 0, 'alpha', 0, 'a', 0.4, 'qlim', initialPose_left(2)+deg2rad([-90 +90])); 
% -178 +178 
baseL = [1 0 0 0;  
        0 1 0 0;  
        0 0 1 0;  
        0 0 0 1]; 

1 (. 1) . 

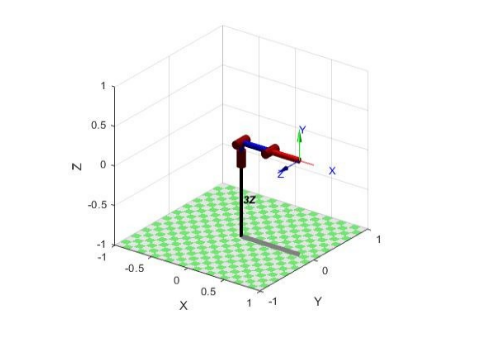
 Tetta, .  initialPose_left. 

. , . 

, .  

  . :

q – . 

%       
t1_min = L(1).qlim(1); t1_max = L(1).qlim(2);  
t2_min = L(2).qlim(1); t2_max = L(2).qlim(2); 
t3_min = L(3).qlim(1); t3_max = L(3).qlim(2); 
%     
t1 = t1_min + (t1_max-t1_min)*rand(N,1); 
t2 = t2_min + (t2_max-t2_min)*rand(N,1); 
t3 = t3_min + (t3_max-t3_min)*rand(N,1); 
Y = horzcat(t1, t2, t3);

, .  : 

:  x,y,z – . R – , . 

%    4x4 
T = zeros(4, 4, N); 
T(:, :, :) = leftArm.fkine(Y); %  ,       
%R = tr2rpy(T(1:3, 1:3, :), 'arm'); %      
R = tr2eul(T(1:3, 1:3, :)); %      
Tx = reshape(T(1, 4, :), [N 1]); %  - 
Ty = reshape(T(2, 4, :), [N 1]); 
Tz = reshape(T(3, 4, :), [N 1]); 
% scatter3(Tx,Ty,Tz,'.','r'); 
X = horzcat(Tx, Ty, Tz, R); %   

. 3.2.1  , 3000 . 

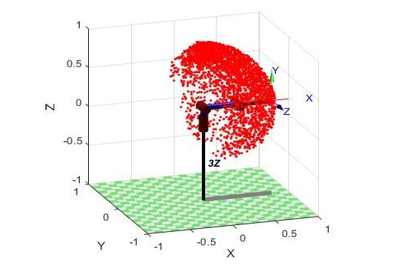
, 3000 . , X Y. 

, .

Keras Python. .

X_train, X_test, y_train, y_test = train_test_split(data_x, data_y, test_size=0.2,
random_state=42) 

« » . .

def base_model():
 model = Sequential()
 model.add(Dense(32,input_dim=6,activation='relu'))
 model.add(Dense(64,activation='relu'))
 model.add(Dense(128,activation='relu'))
 model.add(Dense(32,activation='relu'))
 model.add(Dense(3, init='normal'))
 model.compile(loss='mean_absolute_error', optimizer = 'adam', metrics=['accuracy'])
 model.summary()
 return model

, . . , , . , , .       KerasRegressor,  Keras.

clf = KerasRegressor(build_fn=base_model, epochs=500, batch_size=20,verbose=2)
clf.fit(X_train,y_train) 

.

res = clf.predict(X_test) 

99% , . 

3 , , , . . , . . - . , , , , .

%%    ,    
M=[-178:10:178]; %      -178   +178    10 
M_size=length(M); 
first_q=zeros(M_size, 3); 
T33 = zeros(4, 4, M_size); 
T34 = zeros(4, 4, M_size); 
first_q(:,1)=[deg2rad(M)]; %  q 
T33(:, :, :) = leftArm.fkine(first_q);%      ,   
R = tr2rpy(T33(1:3, 1:3, :), 'arm'); %      
Tx = reshape(T33(1, 4, :), [M_size 1]); %  - 
Ty = reshape(T33(2, 4, :), [M_size 1]); 
Tz = reshape(T33(3, 4, :), [M_size 1]); 
plot3(Tx,Ty,Tz) 
axis([-1 1 -1 1 -1 1]);hold on;grid on; 

XX = horzcat(Tx, Ty, Tz, R); %        
T34(:, :, :) = leftArm.fkine(q_new); %     ,   
Tx2 = reshape(T34(1, 4, :), [M_size 1]); %  - 
Ty2 = reshape(T34(2, 4, :), [M_size 1]); 
Tz2 = reshape(T34(3, 4, :), [M_size 1]); 
plot3(Tx2,Ty2,Tz2,'.') 
axis([-1 1 -1 1 -1 1])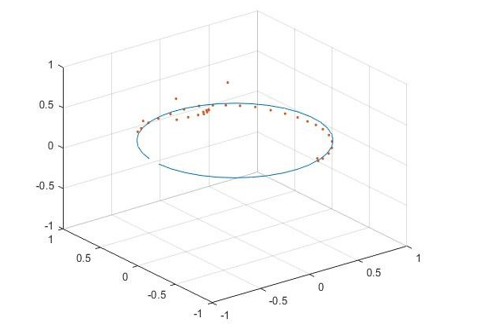 

. . , - . , . . «Programming by demonstration», . Matlab , – .