Objectif et portée de l'horizon artificiel
Un horizon artificiel au sens étroit considéré ici est une visualisation de l'inclinaison d'un objet par rapport à la verticale locale, utilisée pour contrôler son mouvement. La pente est définie par les valeurs des deux angles d'Euler, roulis et tangage . Les marins préfèrent le synonyme «assiette» au terme aéronautique «pitch».
Lié à l'horizon artificiel (mais pas tout à fait synonyme), les termes de la langue russe: "horizon artificiel", "appareil de commande de vol". En anglais, les expressions «indicateur d'attitude» , «horizon artificiel» ou «gyro horizon» sont utilisées .
Techniques de visualisation connues
La plupart des travaux visant à trouver des solutions efficaces dans le domaine de l’indication de tangage et de roulis ont été réalisés dans l’intérêt de l’aviation. Il y a une explication simple à cela: le pilote doit lire les informations rapidement, et toute erreur dans sa perception de l'espace risque de devenir fatale.
La plupart des solutions connues dans le domaine de l'indication de roulis et de tangage reposent sur l'utilisation d'une silhouette d'aéronef et d'un arrière-plan particulier. Caractéristiques générales:
- le fond est divisé en deux parties, symbolisant le ciel et la terre, par une ligne représentant l'horizon;
- la silhouette de l'avion est une vue arrière simplifiée, contrastant en couleur avec l'arrière-plan;
- l'angle de roulis est déterminé par l'indicateur comme l'angle entre la ligne d'horizon symbolique et la ligne reliant les extrémités des ailes de la silhouette (généralement une échelle de référence est présente pour une lecture précise);
- l'angle de tangage est mesuré selon une échelle perpendiculaire à l'horizon conditionnel en fonction de la position du point de contrôle au centre de la silhouette.

Les systèmes mis en œuvre dans la production de masse ont un certain nombre de solutions communes:
- l'information est donnée par la position relative de la silhouette et du fond;
- le changement d'angle de roulis est associé au mouvement angulaire de la silhouette par rapport au fond;
- le changement d'angle de pas est associé au déplacement linéaire de la silhouette par rapport au fond.
Mais il n'est pas difficile de deviner que le mouvement relatif souhaité peut être réalisé de plusieurs manières différentes. Après de nombreux essais et erreurs du siècle dernier, l'évolution de l'aviation a laissé deux combinaisons viables:
1. Silhouette fixe, se déplaçant en arrière-plan de roulis et de tangage. Noms utilisés: "indication directe", "vue du plan vers le sol", moins souvent "indication égocentrique".
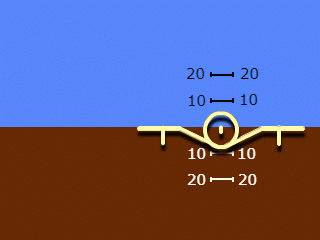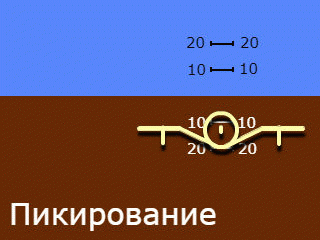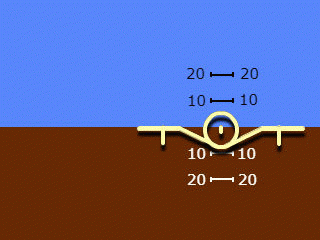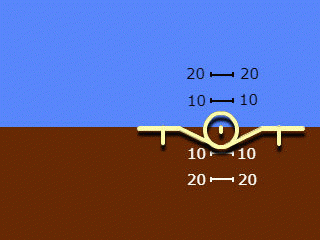
2. Une silhouette se déplaçant uniquement le long du rouleau, un arrière-plan se déplaçant uniquement le long du terrain. Noms utilisés: "indication inverse" et "vue du sol vers le plan", moins souvent "indication géocentrique".

Notez que les noms de la clause 2 s'appliquent au système dans son ensemble, mais reflètent uniquement le principe d'indication de l'angle de roulis qui y est adopté. L'indication de l'angle de pas dans les deux systèmes utilisés est "droite" et "égocentrique".
Dans les simulateurs de vol existants, tels que Microsoft Flight Simulator et Digital Combat Simulator , les deux types d'écrans peuvent être vus en action.
Il convient de noter que toutes les solutions connues ne correspondent pas au schéma ci-dessus. Pour un exemple de dépassement du cadre désigné, considérons deux brevets d'invention: RU 2561311 et RU 2331848.
Le premier brevet est consacré à "Horizon artificiel avec indicateurs de tangage et de roulis espacés en hauteur", ses auteurs: V. I. Putintsev et N. A. Lituev. Le diagramme ci-dessous est repris du brevet.

Si nécessaire, vous pouvez trouver un décodage des désignations et une description de l'œuvre dans le texte de la source originale... Dans l'ensemble, l'idée de l'invention est assez simple: l'idée d'une «vue du sol vers un avion» se réalise à la fois en roulis et en tangage («géocentrisme complet»), mais l'indication est divisée en deux composantes indépendantes.
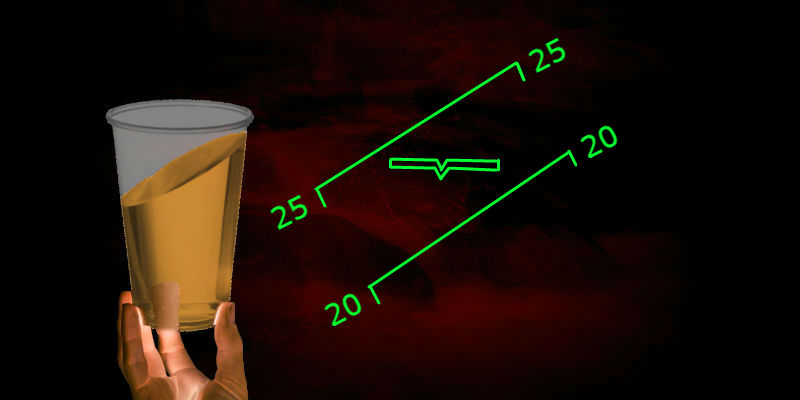
La deuxième invention a un nom plus complexe: "Dispositif de commande de vol pour indication logique de la position et du contrôle de l'aéronef dans l'espace". Auteurs du brevet: A.P. Plentsov et N.A. Zakonova L'idée d'indication de tangage et de roulis est ici assez inhabituelle.
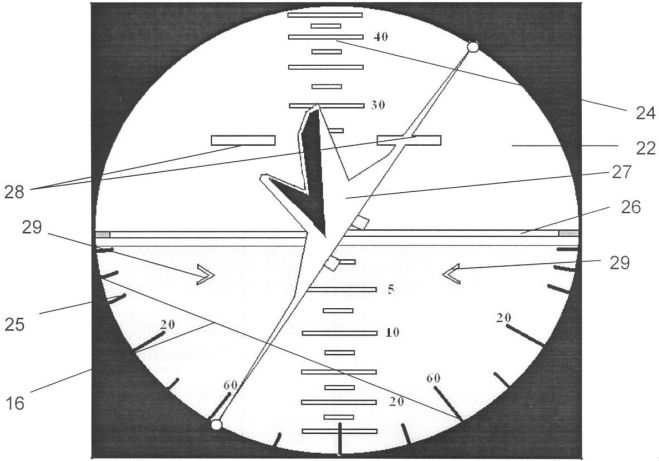
Une explication des désignations du circuit, une description du dispositif, une comparaison avec des analogues et des circuits supplémentaires avec de légères différences de conception sont données dans le brevet .
Une chose en commun avec l'invention précédente est le concept de géocentrisme pour les deux canaux. En même temps, l'horizon artificiel n'a qu'un seul «symbole d'avion», comme dans les modèles existants, mais ce n'est plus une silhouette, mais un modèle tridimensionnel - un «modèle volumétrique». Si le mouvement de roulis s'avère similaire à celui mis en œuvre dans l'indication «inverse», alors le tangage et la plongée sur cet appareil semblent originaux.

Un certain nombre de facteurs freinent l'innovation dans la conception de systèmes d'affichage réels. Par exemple, l'un des motifs raisonnables de conservatisme est la volonté de préserver la continuité des compétences acquises par l'opérateur, y compris les compétences de perception de l'information. Les jeux informatiques peuvent offrir beaucoup plus de créativité, par conséquent, sans se plonger dans une analyse comparative des solutions, nous prendrons comme base l'invention qui semble la plus efficace.
Exigences de la solution
Avant de commencer à écrire le code, définissons la tâche:
1. Il est nécessaire d'écrire la fonction drawAttitude () qui dessine l' indicateur d'horizon artificiel à l' aide de canvas basé sur l'invention de A.P. Plentsov et N.A. Zakonova
2. La fonction prend le contexte du canvas , les coordonnées le centre de l'indicateur, les valeurs des angles de roulis et de tangage en degrés, le rayon de la face de l'indicateur.
3. Les valeurs de l'angle de tangage sont limitées à l'intervalle de moins 30 à plus 30 degrés.
4. Les valeurs de l'angle de roulis sont limitées à l'intervalle de moins 45 à plus 45 degrés.
5. Si la valeur de l'argument dépasse celles spécifiées dans p. 3 et 4 limites l'indicateur montre la valeur autorisée la plus proche.
Création de fonction
Le code de fonction comprend les parties suivantes:
1. Vérification des valeurs entrées pour le dépassement des limites.
2. Conversion des angles en radians.
3. Mise à l'échelle de la taille caractéristique de la "mise en page" et de la police par la valeur du rayon de l'indicateur.
4. Composants du dessin:
a) Corps de l'indicateur.
b) Disposition.
c) Échelles de tangage et de roulis.
La fonction ci-dessous est écrite dans cet ordre et ses parties sont séparées par des commentaires.
Code complet
Code de fichier HTML :
attitude.js:
<!DOCTYPE html>
<html>
<head>
<title>Attitude</title>
<script src="js/attitude.js"></script>
</head>
<body>
<canvas id="drawingCanvas" width="640" height="480"></canvas>
</body>
</html>attitude.js:
window.onload = function () {
let canvas = document.getElementById("drawingCanvas");
let context = canvas.getContext("2d");
let run = function () {
drawAttitude(context, 320, 240, 30 * Math.sin(performance.now() / 2000), 45 * Math.sin(performance.now() / 5000), 200);
}
let interval = setInterval(run, 1000 / 60);
};
drawAttitude = function (ctx, centreX, centreY, pitch, roll, radius = 100) {
// :
if (pitch > 30) pitch = 30;
if (pitch < -30) pitch = -30;
if (roll > 45) roll = 45;
if (roll < -45) roll = -45;
// :
roll *= Math.PI / 180;
pitch *= Math.PI / 180;
// "" :
let vehicleSize = radius * 0.8;
ctx.font = Math.round(radius / 8) + "px Arial";
// :
ctx.lineWidth = 2;
ctx.strokeStyle = "Black";
// :
ctx.beginPath();
ctx.arc(centreX, centreY, radius, 0, Math.PI, false);
ctx.fillStyle = "Maroon";
ctx.stroke();
ctx.fill();
// :
ctx.beginPath();
ctx.arc(centreX, centreY, radius, 0, Math.PI, true);
ctx.fillStyle = "SkyBlue";
ctx.stroke();
ctx.fill();
//"":
ctx.beginPath();
//:
let topSideIsVisible = (pitch >= 0);
ctx.strokeStyle = topSideIsVisible ? "Orange" : "Brown";
ctx.fillStyle = topSideIsVisible ? "Yellow" : "Red";
ctx.lineWidth = 3;
//
// 4 , ,
// :
ctx.moveTo(centreX, centreY - Math.sin(pitch) * vehicleSize / 2);
ctx.lineTo(centreX + vehicleSize * Math.cos(roll), centreY + vehicleSize * Math.sin(roll) * Math.cos(pitch));
ctx.lineTo(centreX, centreY - 2 * Math.sin(pitch) * vehicleSize);
ctx.lineTo(centreX - vehicleSize * Math.cos(roll), centreY - vehicleSize * Math.sin(roll) * Math.cos(pitch));
ctx.lineTo(centreX, centreY - Math.sin(pitch) * vehicleSize / 2);
ctx.stroke();
ctx.fill();
// :
// :
ctx.beginPath();
ctx.strokeStyle = "Black";
ctx.fillStyle = "Black";
ctx.lineWidth = 1;
//:
ctx.fillText(30, centreX - radius * 0.28, centreY - vehicleSize + radius / 20);
ctx.fillText(20, centreX - radius * 0.28, centreY - vehicleSize * 0.684 + radius / 20);
ctx.fillText(10, centreX - radius * 0.28, centreY - vehicleSize * 0.348 + radius / 20);
// - :
ctx.moveTo(centreX - radius / 10, centreY - vehicleSize);
ctx.lineTo(centreX + radius / 10, centreY - vehicleSize);
ctx.stroke();
ctx.moveTo(centreX - radius / 10, centreY - vehicleSize * 0.684);
ctx.lineTo(centreX + radius / 10, centreY - vehicleSize * 0.684);
ctx.stroke();
ctx.moveTo(centreX - radius / 10, centreY - vehicleSize * 0.348);
ctx.lineTo(centreX + radius / 10, centreY - vehicleSize * 0.348);
ctx.stroke();
// :
ctx.beginPath();
ctx.strokeStyle = "White";
ctx.fillStyle = "White";
//:
ctx.fillText(30, centreX - radius * 0.28, centreY + vehicleSize + radius / 20);
ctx.fillText(20, centreX - radius * 0.28, centreY + vehicleSize * 0.684 + radius / 20);
ctx.fillText(10, centreX - radius * 0.28, centreY + vehicleSize * 0.348 + radius / 20);
// - :
ctx.moveTo(centreX - radius / 10, centreY + vehicleSize);
ctx.lineTo(centreX + radius / 10, centreY + vehicleSize);
ctx.stroke();
ctx.moveTo(centreX - radius / 10, centreY + vehicleSize * 0.684);
ctx.lineTo(centreX + radius / 10, centreY + vehicleSize * 0.684);
ctx.stroke();
ctx.moveTo(centreX - radius / 10, centreY + vehicleSize * 0.348);
ctx.lineTo(centreX + radius / 10, centreY + vehicleSize * 0.348);
ctx.stroke();
// :
ctx.lineWidth = 2;
//+-15 :
ctx.fillText(15, centreX + radius * 0.6, centreY + radius * 0.22);
ctx.moveTo(centreX + 0.966 * 0.8 * radius, centreY + 0.259 * 0.8 * radius);
ctx.lineTo(centreX + 0.966 * 0.95 * radius, centreY + 0.259 * 0.95 * radius);
ctx.fillText(15, centreX - radius * 0.75, centreY + radius * 0.22);
ctx.moveTo(centreX - 0.966 * 0.8 * radius, centreY + 0.259 * 0.8 * radius);
ctx.lineTo(centreX - 0.966 * 0.95 * radius, centreY + 0.259 * 0.95 * radius);
//+-30 :
ctx.moveTo(centreX + 0.866 * 0.8 * radius, centreY + 0.5 * 0.8 * radius);
ctx.lineTo(centreX + 0.866 * 0.95 * radius, centreY + 0.5 * 0.95 * radius);
ctx.moveTo(centreX - 0.866 * 0.8 * radius, centreY + 0.5 * 0.8 * radius);
ctx.lineTo(centreX - 0.866 * 0.95 * radius, centreY + 0.5 * 0.95 * radius);
//+-45 :
ctx.moveTo(centreX + 0.707 * 0.8 * radius, centreY + 0.707 * 0.8 * radius);
ctx.lineTo(centreX + 0.707 * 0.95 * radius, centreY + 0.707 * 0.95 * radius);
ctx.moveTo(centreX - 0.707 * 0.8 * radius, centreY + 0.707 * 0.8 * radius);
ctx.lineTo(centreX - 0.707 * 0.95 * radius, centreY + 0.707 * 0.95 * radius);
ctx.stroke();
}Le plus difficile à comprendre est le code pour dessiner la «mise en page». Examinons cela plus en détail. Comme mise en page, il a été décidé d'utiliser une figure symétrique plate en forme de flèche.
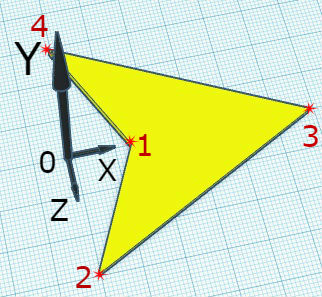
Les surfaces supérieure et inférieure de la mise en page diffèrent l'une de l'autre par le contour et la couleur de remplissage. Le choix de la palette de couleurs actuelle est la première partie du code.
Vient ensuite la construction du contour de la figure.
La tâche la plus difficile est de déterminer les coordonnées des projections des sommets de la figure sur le plan YOZ . C'est ce que résolvent les expressions avec des fonctions trigonométriques. Les sommets du code sont parcourus dans l'ordre de leur numérotation dans la figure.
La plus grande partie du code est consacrée aux échelles et aux signatures. Les marques d'échelle présentent de nombreuses différences: haut et bas, gauche et droite, avec et sans étiquettes. Le nombre impressionnant de lignes est dû à l'écriture du code "individuel" pour chaque élément.
Les fonctions trigonométriques des angles correspondants sont utilisées pour appliquer des marques de roulis. Puisque les valeurs des angles de chaque étiquette sont connues à l'avance, des valeurs prêtes à l'emploi des sinus et des cosinus sont écrites dans le code.
Il est préférable d'évaluer le type d'indicateur en dynamique. Montrons les oscillations de pitch and roll en utilisant la nouvelle fonction. Pour la variété maximale de positions, rendons les amplitudes d'oscillation correspondant aux limites de l'indicateur et les périodes - différentes et mutuellement simples.
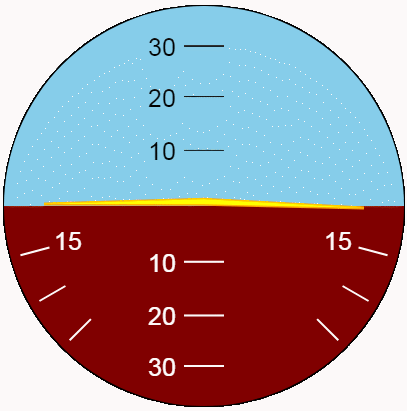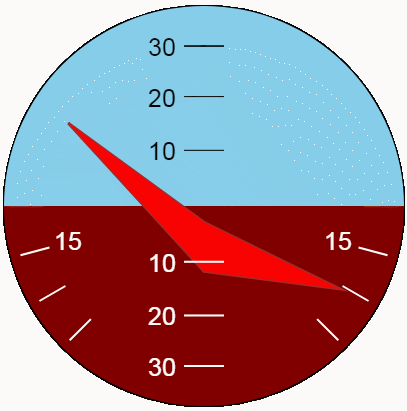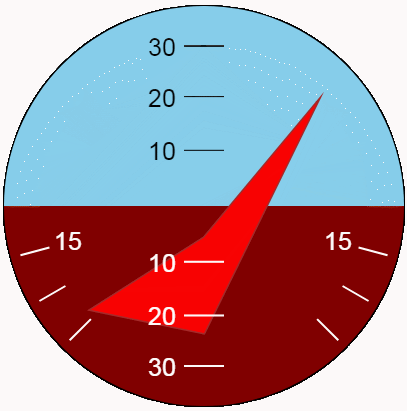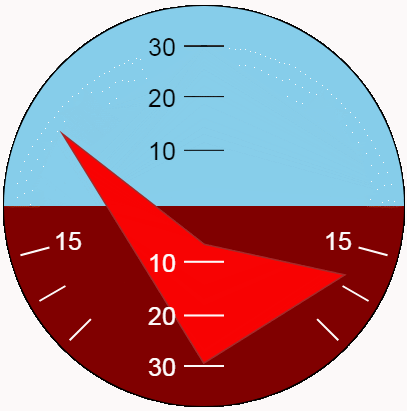
Conclusion
Strictement parlant, le code ci-dessus pour la visualisation du roulis et du tangage doit être appelé une indication "basée sur" l'invention de A. P. Plentsov et N. A. Zakonova. Certaines dérogations aux schémas originaux sont faites pour simplifier le problème, d'autres pour améliorer la mise en œuvre.
L'indicateur présenté est loin d'être idéal en termes de design. Les limitations acceptées des valeurs affichées ne sont optimales pour aucun critère objectif. Néanmoins, la tâche de créer un démonstrateur d'une technologie intéressante peut être considérée comme résolue.