Comment confronter les mathématiciens et les spécialistes du ML à l'aide d'un hackathon, et qui gagnera alors

introduction

Cet article explique comment nous, avec la filiale de Rosneft Samaraneftekhimproekt et l'Université fédérale de Kazan, avons organisé le Hackathon des trois villes en septembre 2020, où nous avons invité des étudiants à résoudre le problème classique de la corrélation sismique des horizons réfléchissants. Tels sont les défis auxquels les professionnels de la sismique du monde entier sont confrontés au quotidien. Pour les participants, il a été décidé de présenter la tâche comme «la tâche de trouver le chemin optimal» afin de ne pas effrayer les élèves avec des mots terribles. Dans l'article, nous vous en dirons plus sur le problème et analyserons les solutions intéressantes des participants. Ce sera passionnant à la fois pour la modélisation mathématique appliquée et l'apprentissage automatique et les analystes de données.

Partie organisationnelle

Nous avons décrit des détails intéressants sur l'organisation d'un hackathon en ligne dans trois villes dans un article sur vc.ru - Oil and Hackathon. Un marathon ne consiste pas seulement à courir .

Nous mentionnerons seulement que pour le format en ligne nous avons choisi le service Discord et laisserons un lien vers les règles du hackathon (lien sur le site Boosters ).

Formulation du problème

Dans l'exploration sismique, il y a le concept d '«horizon sismique réfléchissant» - c'est une onde réfléchie, stable en dynamique et en zone de propagation, qui correspond à une certaine limite géologique. En traitant correctement les données sismiques de terrain et en reconnaissant (disent les experts en prospection sismique - "interpréter") les horizons sismiques, il est possible de déterminer la profondeur de leur occurrence avec une précision de 5 à 10 mètres. Après avoir déterminé les profondeurs, il est alors possible, avec les géologues, de lier ces horizons à l'échelle géochronologique ( échelle géochronologique - Wikipedia ) et de reconnaître leurs homologues plus petits. Et puis décidez - entre quels horizons les pièges à pétrole peuvent se trouver, à quoi ressemble le relief du modèle structurel du champ, etc.







Les sections verticales du cube sismique et reconnu horizons sismiques reflétant



Dans la pratique, les horizons sont identifiés couche par couche sur les sections sismiques du cube sismique - les deux manuellement, utilisant un réseau (experts sismiques disent - « plongée ») un grand nombre de points de référence, et en utilisant des procédures de recherche automatiques et semi-automatiques ... Bien entendu, une solution de haute qualité au problème de l'interprétation des horizons sismiques à l'aide de logiciels est très demandée et peut réduire considérablement le temps passé par les spécialistes de la prospection sismique.



Parallèlement, l'étude des sources ( horizons des moindres carrés avec pentes locales et corrélations multi-mailles, Waveform Embedding: sélection automatique d'horizon avec apprentissage profond non supervisé) montre que les algorithmes et solutions développés sont basés sur un petit nombre d'approches mathématiques, nous avons donc décidé d'essayer d'attirer les étudiants avec leur conscience non encore obscurcie par la recherche scientifique et de leur proposer ce problème sous la forme d'un problème de recherche du chemin optimal sur une surface complexe.

En conséquence, le problème a été formulé comme suit: construction d'un chemin de mouvement sur une surface complexe, passant par des points donnés et satisfaisant les conditions pour un minimum de certaines fonctionnelles, en fonction de la longueur du chemin et de ses angles (gradients).





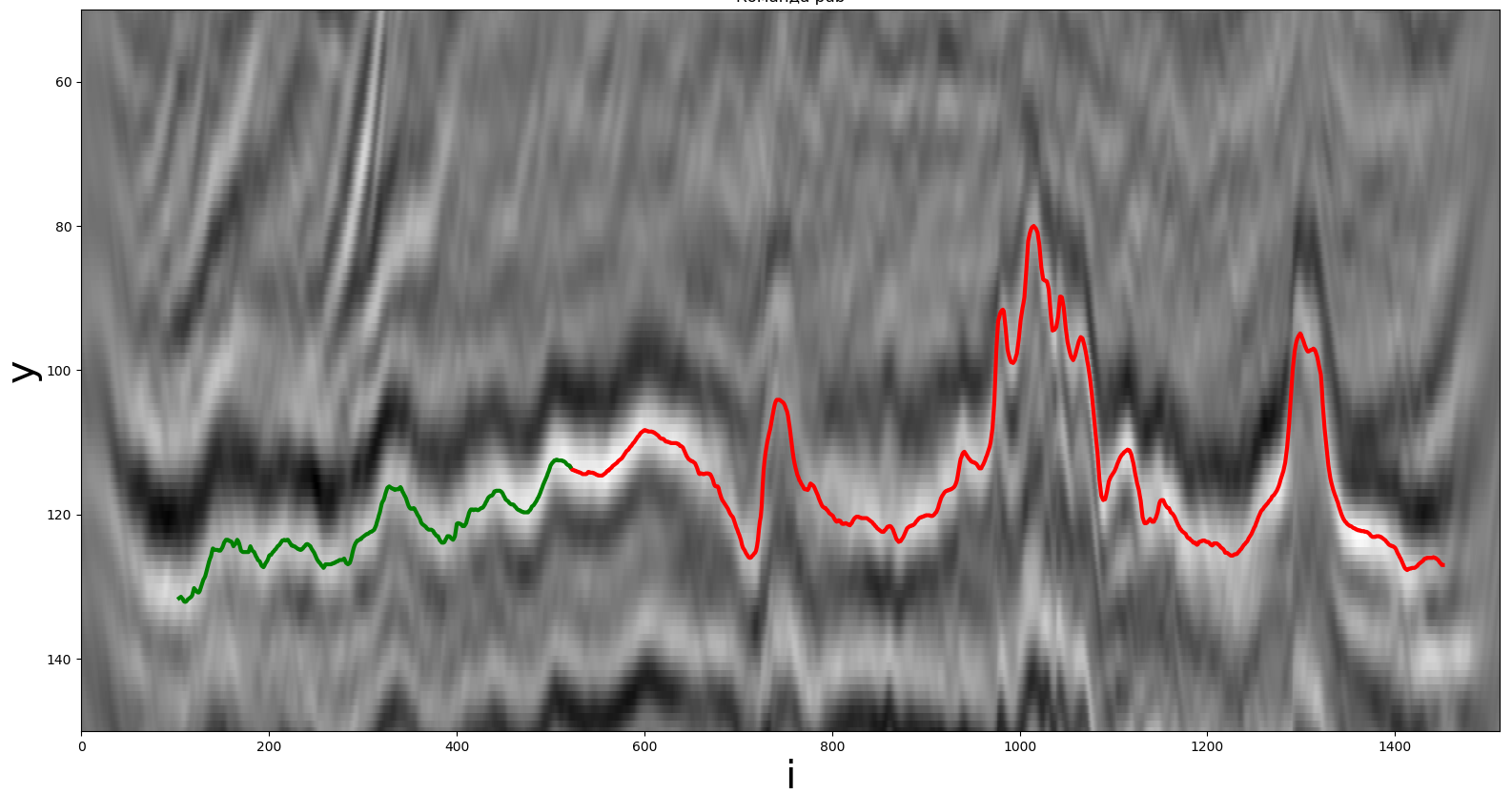
Un exemple d'une partie de la section sismique originale pour la construction d'un horizon. La ligne verte est la pièce connue à l'avance, la ligne rouge est la pièce souhaitée.



Les participants au concours devaient trouver une solution en 12 heures qui leur permettrait de poursuivre leur voyage le long de la trajectoire optimale sur la partie cachée du jeu de données. Il y a eu 20 tentatives pour valider la solution; le participant avec la valeur métrique minimale a gagné.





Tout au long de la compétition, le classement a été construit sur la base des valeurs métriques dans la partie publique des données de test. Après la fin de la compétition, la valeur de la métrique a été recalculée dans la partie privée et le classement a été mis à jour. Ceci est important pour obtenir des solutions durables, c'est-à-dire non seulement adaptées aux données publiques, mais également capables de montrer un résultat comparable sur des données privées. Il s'est avéré que cela n'a pas été fait en vain, et après l'évaluation finale de la qualité, le classement a changé.

Pour quantifier les résultats obtenus, la métrique suivante a été utilisée:

$$

$$F\left (\widehat{y},\widehat{z} \right ) = \sqrt{\sum_{i=0}^N\left(\widehat{y}_{i}^{pred} -\widehat{y}_{i}^{etalon} \right)+\left(\widehat{z}\left(i,y_i^{pred}\right) - \widehat{z}\left(i,y_i^{etalon} \right) \right)^2}$$

où:

N est la dimension de l'horizon requis;

$$${y}_{i}^{pred}$ - les coordonnées de l'horizon, obtenues à l'aide de l'algorithme, $$$i\in\overline{0,N}$;

$$${y}_{i}^{etalon}$ - coordonnées de l'horizon de référence;

$$$\widehat{z}\left(i,y_i\right)$ - les valeurs de la carte de surface au point de coordonnées i, yi;

$$$\widehat{y}_i = \frac{y_i}{{height}}$, où height est la valeur maximale possible de la coordonnée y de la carte de surface;

$$$\widehat{z}\left(i,y_i\right) = \frac{z\left(i,y_i \right)}{{max \left(z \right)}}$où max (z) est la plus grande valeur de la carte de surface.

Quelles méthodes ont été utilisées par les équipes

Le problème a été initialement sélectionné de manière à pouvoir être résolu de plusieurs manières: directe et inverse (en utilisant respectivement des méthodes mathématiques classiques et des méthodes d'apprentissage automatique).



Du point de vue de l'apprentissage automatique, le problème peut être résolu par deux méthodes:



1) Construction de la régression en

utilisant les paires de points connues ($$$x_i,y_i$), vous pouvez construire un mappage $$$f:\phi \left(x_i \right)\mapsto y_i$ en minimisant la fonction de perte L. $$$\phi \left(x_i \right)$- description indicative du i-ème point.



Par exemple,$$$\phi : x_i \mapsto x_i$ ou $$$\phi : x_i \mapsto \left( x_i,x_i^2,x_i \cdot x \right)$



La fonction de perte peut être soit la fonction d'erreur initiale de l'énoncé du problème, soit une fonction plus simple, par exemple, l'écart type des chemins construits et originaux:

$$

$$\frac{1}{N} \sum_{i=0}^N \left( y_i - \widehat{y}_i \right)^2$$

De nombreuses méthodes d'apprentissage automatique populaires peuvent être utilisées pour construire le mappage f : en commençant par la régression polynomiale, en parcourant une forêt aléatoire et des réseaux de neurones profonds.



Plusieurs équipes ont adopté cette approche en utilisant comme$$$\phi$réseau de neurones convolutif ou entièrement connecté, et en tant que réseau de neurones f ou processus gaussiens.



2) Segmentation sémantique





Un exemple de segmentation sémantique



Le problème original peut être résolu comme un problème de vision par ordinateur. Les points (x, y) sont considérés comme des pixels d'image, où l'image entière est l'ensemble de données entier, et la "luminosité" du pixel (x, y) est la valeur z (x, y). Pour construire un chemin, vous devez attribuer l'une des classes à chaque pixel - 0 ou 1. La partie de l'image qui se trouve sous le chemin ou qui l'inclut appartient à la classe 0, et le reste appartient à la classe 1. La solution quotidienne à un tel problème est un réseau de neurones entièrement convolutif U-Net, sur une entrée qui reçoit un morceau (patch) de l'image originale et produit un tableau de même taille, composé de zéros et de uns, indiquant les classes des pixels correspondants.



En plus des techniques d'apprentissage en profondeur, vous pouvez également utiliser des techniques classiques de vision par ordinateur et de traitement d'image telles que le remplissage par inondation pour la segmentation d'image. Cela a été fait par l'un des participants, prétraitant ainsi l'image pour une application ultérieure des algorithmes pour trouver le chemin le plus court.



Du point de vue des méthodes mathématiques classiques, le problème proposé est un problème d'optimisation classique, et nous avons observé des tentatives pour le résoudre par les groupes de méthodes suivants:

1. , ;
   
   
   
   . y , y, .
2. , ;
   
   
   
   $$$y_i$ .
3. , .
   
   
   
   , .

Tout d'abord, analysons les décisions des participants.



Méthodes d'apprentissage automatique: l'

une des solutions était un réseau de neurones convolutif autorégressif qui produit un nombre réel - la valeur du chemin$$$\widehat{y}_i$pour la i-ème étape. Les patchs 32x32 pixels de l'image originale ont été envoyés à l'entrée du réseau neuronal. En tant que fonction$$$\phi$Pour l'extraction de caractéristiques, nous avons utilisé le réseau neuronal convolutif pré-entraîné ResNet34. La représentation des caractéristiques obtenue par ce réseau de neurones a été combinée avec les valeurs de ce chemin des 32 étapes précédentes. Pour prédire 32 étapes supplémentaires, les prédictions précédentes du réseau neuronal ont été utilisées comme valeurs d'horizon précédentes. Le réseau de neurones a été formé par une modification de la descente du gradient stochastique d'Adam avec une diminution exponentielle de l'étape d'optimisation au fur et à mesure de son entraînement. Pour la formation, l'écart absolu moyen a été minimisé (les expériences avec l'écart-type ont donné de pires résultats). Pour éviter le surajustement, un Dropout a été utilisé, c'est-à-dire une remise à zéro aléatoire d'une partie des neurones. Il a fallu environ 10 minutes pour entraîner le réseau neuronal, 20 passages complets sur l'ensemble de données et 720 étapes d'optimisation.





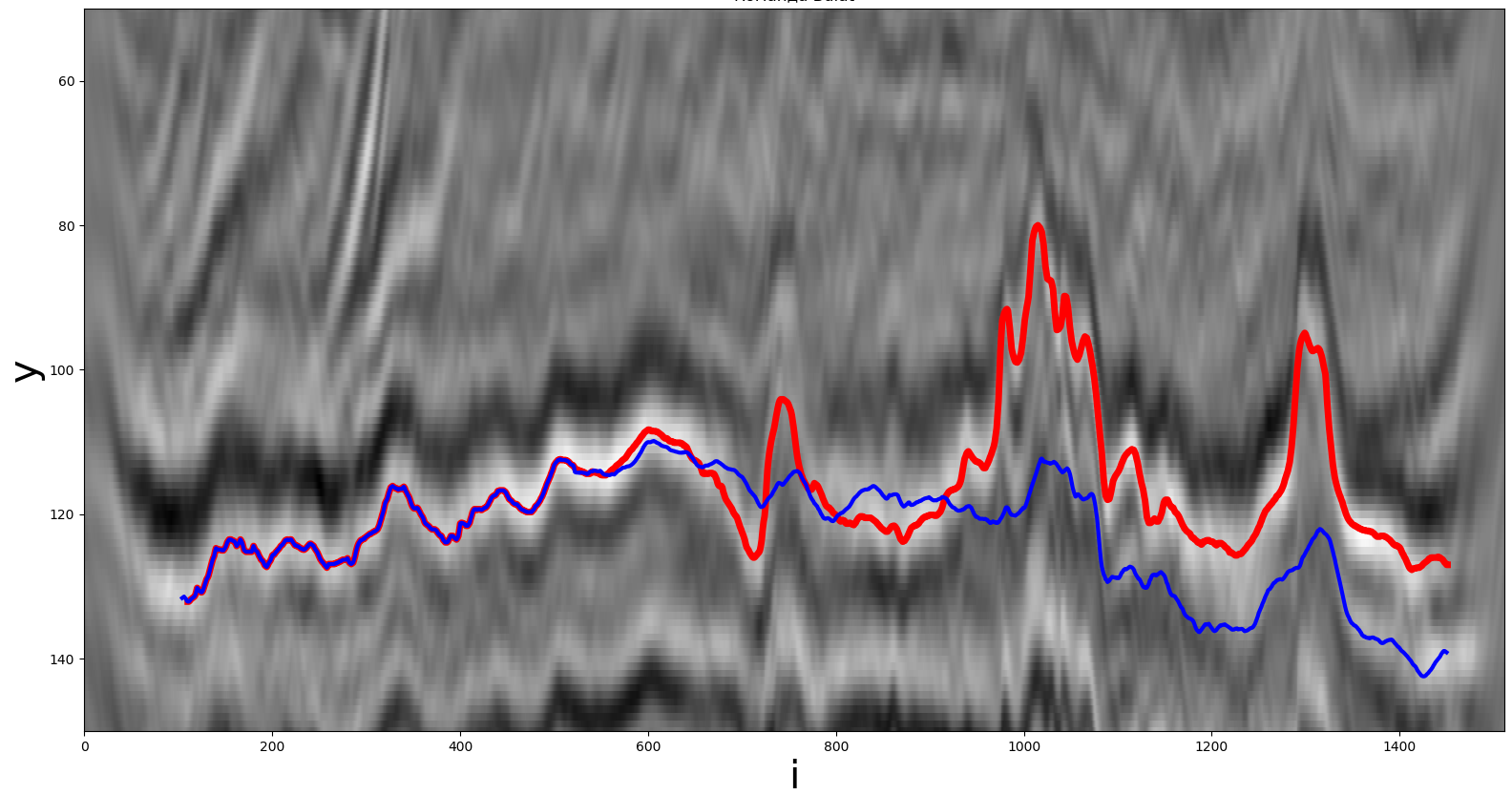
Une solution obtenue à l'aide d'un réseau de neurones convolutifs. La ligne rouge est le vrai chemin, la ligne bleue est celle reçue par le participant.



La prédiction du réseau neuronal prend environ 1 minute sur un processeur AMD Threadripper 2950x et un GPU Nvidia GTX 1080 Ti.



Le résultat du réseau neuronal (métrique) est de 5,71 au classement public. Des expériences ont également été faites avec le remplacement du réseau neuronal convolutif par un réseau récurrent, mais son résultat était pire. En conséquence, des méthodes classiques de mathématiques computationnelles ont été utilisées comme solution finale.



En plus des solutions finies, les participants ont également partagé leurs idées, qu'ils n'ont pas réussi à mettre en œuvre en raison du calendrier serré du concours et de la complexité de calcul de leurs idées. Certains d'entre eux ont essayé d'appliquer des réseaux de neurones, mais après avoir passé la plupart de leur temps, ils sont passés à des algorithmes plus simples et plus efficaces ou même à la force brute et aux règles, ce qui a finalement donné le meilleur résultat et conduit à des prix.



En outre, un certain nombre de solutions intéressantes sont basées sur les connaissances d'autres disciplines: par exemple, la vision par ordinateur classique et le traitement d'images, la théorie des graphes, l'analyse de séries chronologiques. L'une des équipes a même posé un défi en termes d'apprentissage par renforcement dont vous avez peut-être entendu parler et a proposé une solution, mais n'a malheureusement pas eu le temps de la mettre en œuvre.



Méthodes mathématiques classiques:





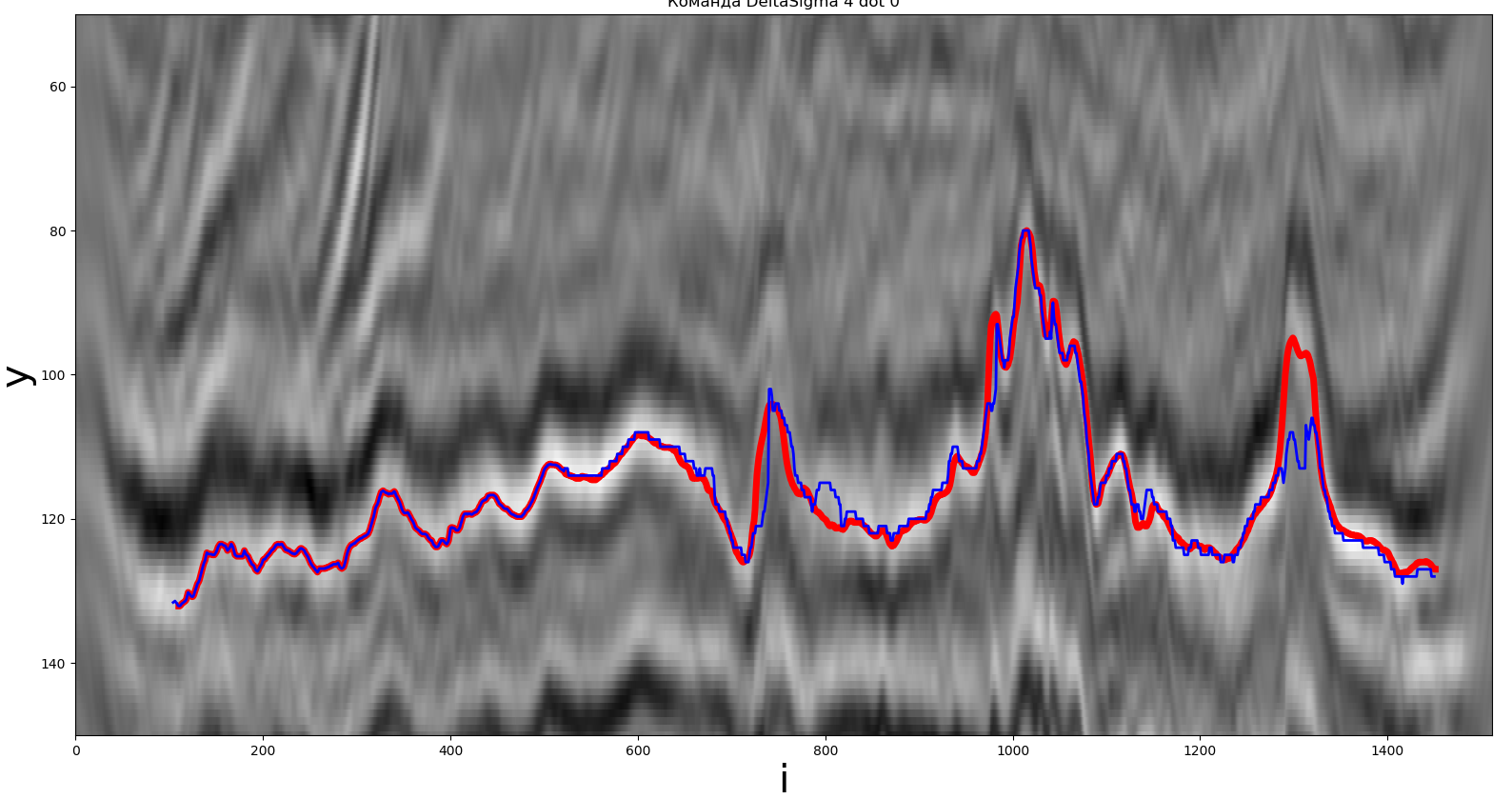
Une des solutions obtenues par la méthode locale extremum. La ligne rouge est le vrai chemin, la ligne bleue est celle reçue par le participant.



Pour cette méthode, un maximum local a été utilisé comme extremum. Le chemin construit par les participants est marqué en bleu, l'horizon souhaité est en rouge. Une description détaillée est fournie ci-dessous.



$$$y_{i+1} = min \left| j-y_i \right|, \forall i \in \overline{0,N-1}, j \in \Omega,$

$$$\Omega = \left \{ m|z(i,m)> z(i,m-1) \cap z(i,m) > z(i,m+1), \forall m \in \overline {m_1,m_2} \right \}$,

$$$m_1 = max(1,y_i - size_y)$,

$$$m_2=min(height - 1,y_i + size_y$,

Où:

$$$height$ - la valeur maximale possible de la coordonnée y de la carte de surface;

$$$size_y$- la taille de la fenêtre de recherche.



La méthode est implémentée en Python. Le temps de fonctionnement était d'environ 0,103 seconde, F (y, z) = 1,57,$$$size_y$= 100.



Conclusion: la méthode est assez simple à mettre en œuvre, le temps d'exécution ne dépasse pas 0,1 seconde.





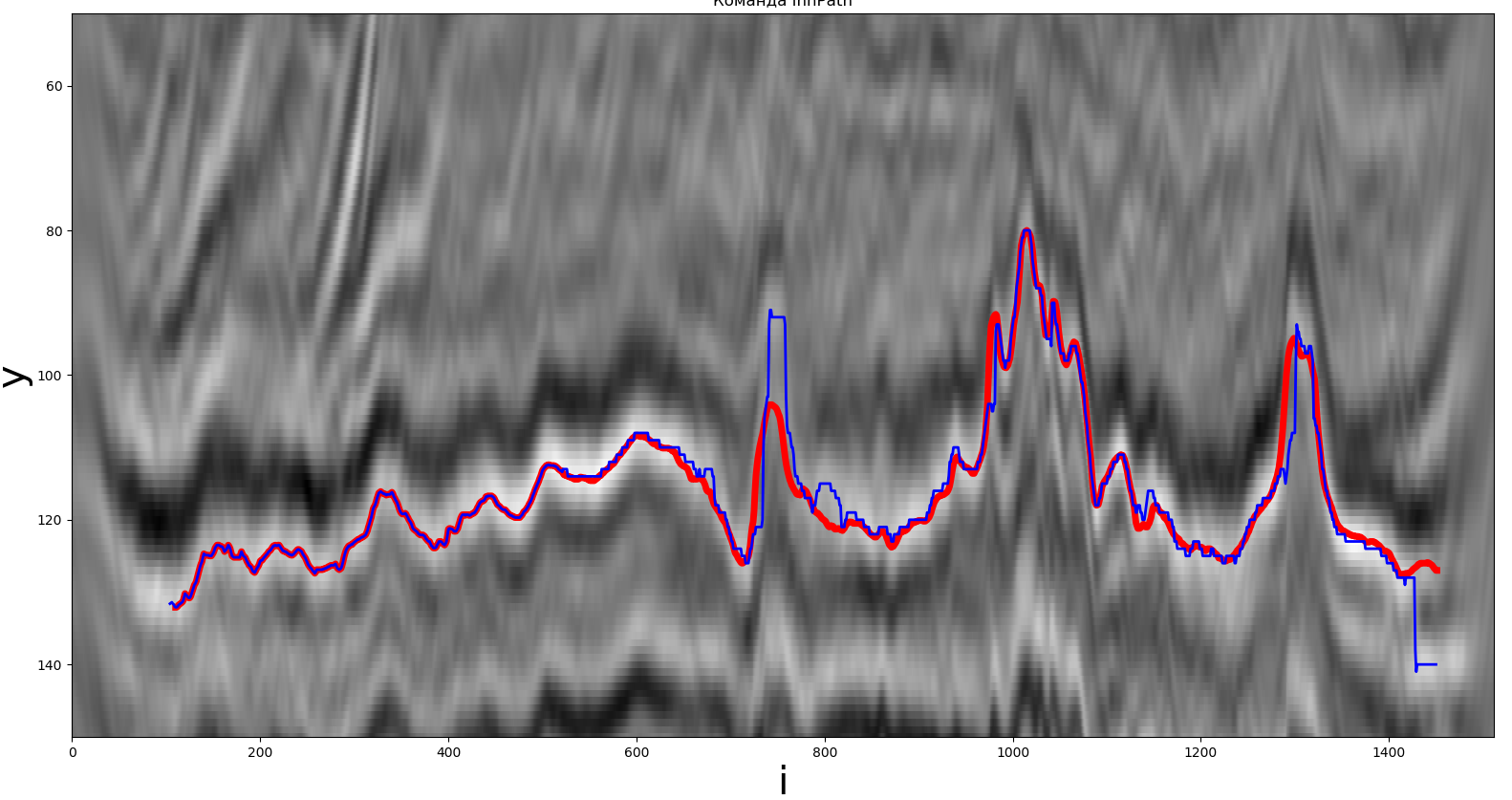
L'une des solutions obtenues par l'extrémum global. La ligne rouge est le vrai chemin, la ligne bleue est celle reçue par le participant.



Passons au groupe suivant. Comme auparavant, dans cette méthode, le maximum a été utilisé comme extrême.



$$$y_i= {argmax}\left(\frac{1}{size_x} \sum_{{j=0}}^{{size_x-1}}z (i+j,m))\right), \forall i \in \overline {0,N}, m \in \overline{m_1,m_2}$,

$$$m_1 = max(1,y_i - size_y)$,

$$$m_2=min(height - 1,y_i + size_y)$,

où:

hauteur est la valeur maximale possible de la coordonnée y de la carte de surface;

$$$size_x,size_y$- la taille de la fenêtre de recherche.



La méthode est implémentée en Python. Le temps de fonctionnement était d'environ 0,19 seconde, F (y, z) = 1,97,$$$size_x$= 9, $$$size_y$= 21.



Conclusion: la méthode est assez simple à mettre en œuvre, le temps de fonctionnement ne dépasse pas 0,2 seconde.





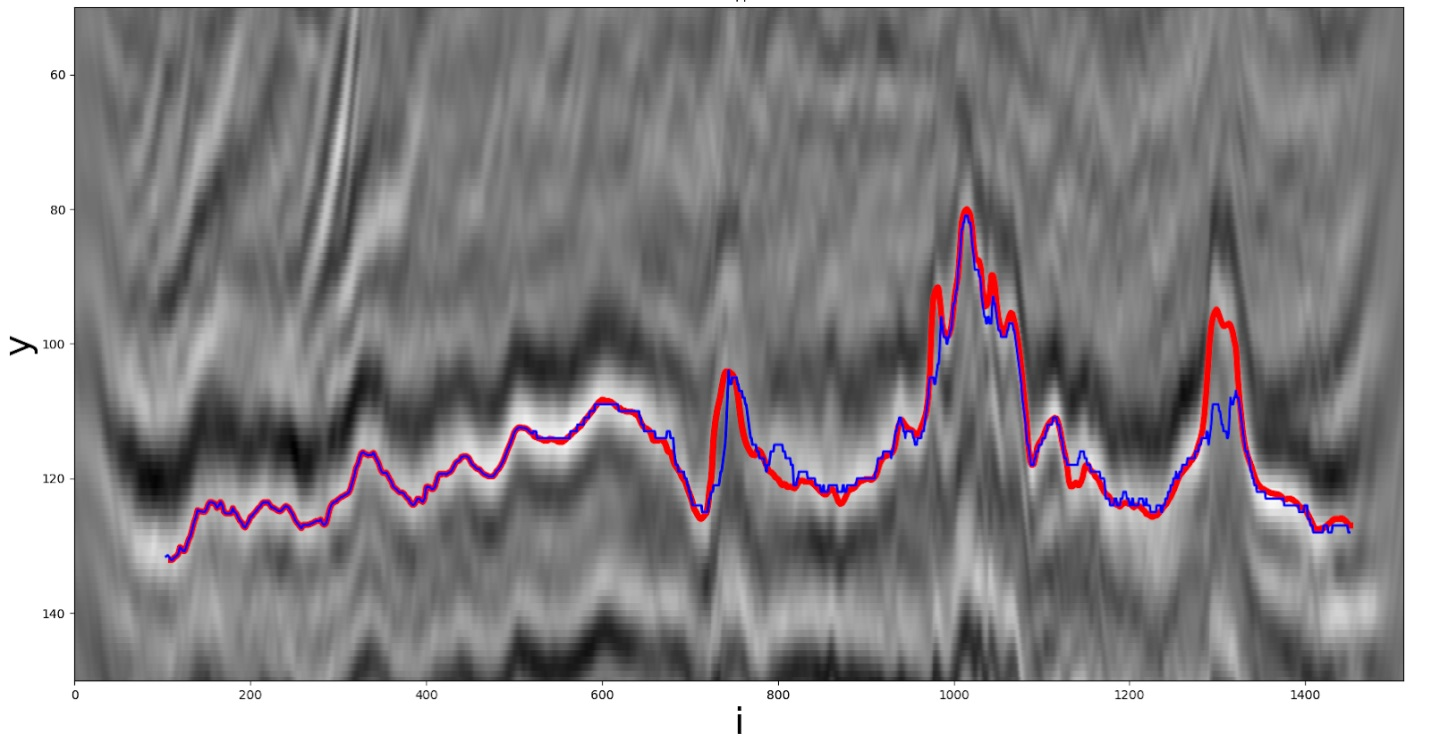
Une des solutions heuristiques. La ligne rouge est le vrai chemin, la ligne bleue est celle reçue par le participant.



Regardons le dernier groupe de méthodes. Comme mentionné précédemment, la coordonnée suivante$$$y_i+1$est recherché par le minimum de fonctionnalités dans la fenêtre de recherche spécifiée.



Voici une des fonctionnalités proposées par les équipes. D'un point de vue mathématique, cela ressemble à ceci:

$$$y_{i+1}= {min}\left(\frac{(z(i,j)-z(i,y_i))^2}{max^2(z)} + \alpha \frac{(j-y_i)^2}{{height}^2}\right), \forall i \in \overline {0,N-1}, j \in \Omega,$

$$$\Omega = \left \{ m|z(i,m)>z(i,m-1)\cap z(i,m)>z(i,m+1), \forall m \in \overline {m_1,m_2} \right \}$

$$$m_1 = max(1,y_i - size_y)$,

$$$m_2=min(height - 1,y_i + size_y)$,

Où:

$$$height$ - la valeur maximale possible de la coordonnée y de la carte de surface;

$$$\alpha$- coefficient responsable de l'influence de l'erreur en y sur la valeur de la fonctionnelle;

$$$size_y$ - la taille de la fenêtre de recherche;

$$$max(z)$Est la valeur la plus élevée de la carte de surface.

La méthode a été implémentée en Python. Le temps de fonctionnement était d'environ 0,12 seconde, F (y, z) = 1,58,$$$size_y$= 50, $$$\alpha$= 15000,7.



Conclusion: la durée de fonctionnement de la méthode ne dépasse pas 0,15 seconde.



Les méthodes des trois groupes ont montré des résultats assez similaires sur un ensemble de données donné. La plus petite valeur métrique (1,57) a été obtenue par une méthode basée sur la recherche d'extrema locaux de valeurs de surface dans une fenêtre de recherche donnée.

Partie finale

Malheureusement, à la fin du hackathon, presque tous les innovateurs sont passés du côté obscur, se sont recyclés et sont devenus conservateurs, c'est-à-dire qu'ils ont commencé à envoyer des solutions utilisant des algorithmes classiques ... et les conservateurs ont gagné.



Nous voulions rassembler des contributeurs de deux domaines: les mathématiques computationnelles et l'apprentissage automatique. Certains sont habitués à travailler avec des données non structurées de nature inconnue, tandis que d'autres sont habitués à étudier les processus physiques et à construire des modèles mathématiques sur leur base. Pour augmenter la variété des idées et des solutions, nous avons brièvement décrit comment les données ont été obtenues. C'est l'une des raisons pour lesquelles la solution basée sur des méthodes numériques simples a donné les meilleurs résultats. La deuxième raison était que pour le hackathon étudiant, nous avons préparé des données pas très "complexes" d'un petit volume, de sorte que les méthodes d'apprentissage automatique modernes et chronophages perdent face à des alternatives plus simples.



Nous pensons que c'est une excellente leçon qui aidera les participants à définir correctement les problèmes et à choisir les meilleures méthodes pour les résoudre. Il est important de se rappeler que vous devez d'abord essayer une solution simple, la soi-disant base de référence, peut-être qu'elle vous permettra d'atteindre votre objectif en peu de temps.



Les participants au Hackathon ont proposé leurs propres algorithmes pour trouver le chemin optimal dans un ensemble de big data en relation avec le problème de l'interprétation cinématique sismique automatique, qui est actuellement en cours de résolution dans le cadre du développement de logiciels d'entreprise dans le domaine de la géologie et de la sismique. Les implémentations d'algorithmes les plus compétitives trouveront leur application dans le développement et l'implémentation de modules logiciels pour ces systèmes logiciels.



Nous serons heureux de vous voir à la finale du marathon de la compétition informatique, qui se tiendra le 28 novembre en ligne. Le programme comprend: la récompense des gagnants du concours, la présentation de la première version de l'application mobile pour une évaluation expresse de la qualité de l'agent de soutènement. Toujours dans le cadre de l'événement, des tables rondes seront organisées sur des thèmes d'actualité "Data and DS Projects Management" et "Computer Vision". Des représentants de Head of Data Science Alfa, CDO Megafon, Huawei, Head of CV X5 et d'autres partageront des cas intéressants.Ne manquez pas tout le plaisir ( IT Competition Marathon 2020 - Rosneft ).