introduction
Le problème cryptographique le plus connu est la transmission de messages secrets. Pour cette tâche, les cryptosystèmes avec une clé privée sont le plus souvent utilisés: Alice (l'expéditeur) crypte les informations à l'aide de la clé et Bob (le destinataire) décrypte le message avec. Malheureusement, les systèmes cryptographiques à clé privée ont de sérieuses difficultés de mise en œuvre pratique. La question principale est de savoir comment distribuer les clés? À bien des égards, la distribution des clés prend autant de temps que la tâche de base de la communication privée. Un tiers malveillant peut écouter la clé et lire facilement le message.
Pour éviter cela, de nombreuses manières ont été inventées, dans cet article nous allons considérer le quantum, dans lequel le secret de la clé est garanti par les lois de la mécanique quantique. Le premier schéma de distribution de clés quantiques (QKD) BB84 a été développé en 1984 par les physiciens Charles Bennett et Gilles Brassard. Son idée principale est d'utiliser le principe de la mécanique quantique (principe d'incertitude), selon lequel l'observation dans son ensemble viole le système observé. Ainsi, l'intercepteur écoutant Alice et Bob «gâte» le message. Ensuite, il peut être facilement calculé et éliminé les «mauvais» bits, et s'il y en a trop, recommencez.
Les bases de la mécanique quantique
Nous n'entrerons pas dans les détails, mais formulons simplement les principaux énoncés. Commençons par le principe d'incertitude. Il dit que certaines grandeurs physiques ne sont absolument pas mesurées exactement. Donnons à titre d'exemple l'élan et la coordonnée d'une particule: si vous mettez une particule dans un appareil qui mesure avec précision la coordonnée (par exemple, il a montré ), puis dans un appareil qui mesure avec précision l'élan, alors le deuxième appareil donnera un nombre aléatoire (que ce soit un nombre
, c'est-à-dire
). Un point important: avant c'était une particule avec une coordonnée
, maintenant c'est une particule avec une impulsion
. Si vous le remettez dans l'appareil mesurant les coordonnées, il donnera un nombre aléatoire.
( , , ). , , .
( ), 2 . , , 4 . ,
,
. BB84.
BB84
:
1) ( )
2)
3)
4)
- ; - ; -

1 .
|
|
(0 1). 0 1 | , , . , , , . |
. ( ). , , , . , "" ( ). - - . , . . BB84 11% [10], . .
. : . , , , (, , ). , , "" . : . (, , ). , , . , .
, :
1) , .
2) , .
BB84, , - -. . A B, C. : . A , B , C . , B , , . , A B. . ( ) .
|
|
, , . , . | , . |
, , 0 1.
. BB84 . BB84 , . , .
.
1
1)
2)
3) ,
, , .
1 . , . , , .
2 . . .
3 . - , . , . , , .
. , , , , . . a) (, , ); ) ; ) ) . "" , .
BB84 [7], . . [8]
H , QBER .
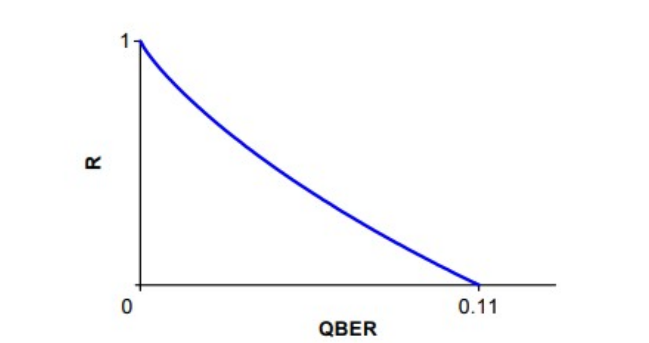
, . . , , . (, , ). , . PNS (photon number splitting)[2]. : , , . , , . , , [1].
2003 , BB84. , SARG04, BB84, . - -, [4]. , [4]. , , -. , . - . , PNS . Lo05[5]. - . ( - GLLP[3]) , . , ( .3).

SARG04[1]. : . ( !!!). , BB84, . , , :
.
( , ).
, , ( ). .
(
)
, ( ).
( 1/4), ,
(
,
,
). PNS : , 1 2 , 3 . [1].
, . SARG04 LPA(large pulse attack). , ( ). . , [6].
, . , . . , id Quantique [9], .4
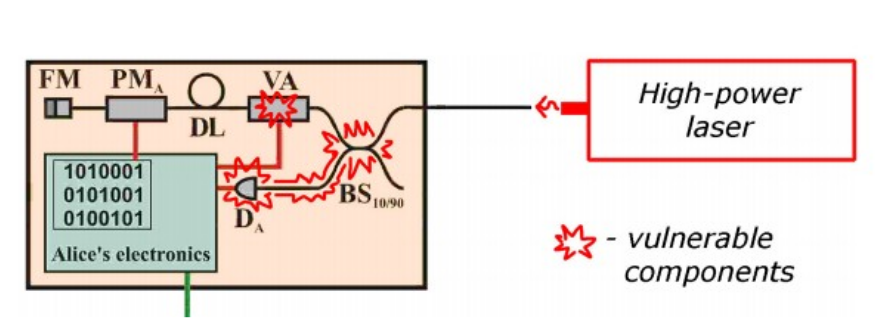
DA, , , . , . , , . ( ). : 1) ; 2) , ; 3) BS (, ); , , , , .
, , . . . . .
, ? : , , , . 1984 - , ? , , (RSA). , 1994 . , . , , .
:
1) A. Acin, N. Gisin, and V. Scarani, “Coherent-pulse implementations of quantum cryptography protocols resistant to photon-number-splitting attacks”
2) C. Bennett, F. Bessette, G. Brassard, L. Salvail, and J. Smolin, “Experimental quantum cryptography”(1992)
3) D. Gottesman, H.-K. Lo, N. L ̈utkenhaus, and J. Preskill, Quant. Inf. Comp. 4, 325 (2004)
4) W.-Y. Hwang, “Quantum key distribution with high loss: toward global secure communication”
5) Lo H., Ma X., Chen K. , “Decoy state quantum key distribution”, (2005)
6) Vadim Makarov, “Quantum cryptography and quantum cryptanalysis ”, (2006)
7) D. Mayers, “Quantum key distribution and string oblivious transfer in noisy channels” (1996); D. Mayers, “Unconditional security in quantum cryptography” (2001).
8) P. Shor et J. Preskill, «Simple preuve de sécurité du protocole de distribution de clé quantique BB84» (2000).
9) D. Stucki, N. Gisin, O. Guinnard, G. Ribordy et H. Zbinden, «Quantum key distribution over 67 km with a plug & play system»
10) Xiaoqing Tan, «Introduction à la cryptographie quantique», (2013)