Clever Geek Handbook

Protocole de distribution de clé quantique AK-15

Salutations à tous ceux qui ont été animés ici par le désir de se renseigner sur l'un des protocoles de cryptographie quantique, car l'apparition éventuelle d'un ordinateur quantique dans un proche avenir mettra en péril de nombreuses méthodes de cryptographie existantes.

Pour le moment, des protocoles ont été proposés, une analyse détaillée dont vous pouvez trouver sur Habré, mais je peux vous recommander un article avec un assez bon aperçu: cliquez ici .

Il convient de noter qu'une caractéristique distinctive de l'AK-15 est la présence d'une authentification entre les utilisateurs légitimes.

introduction

Le protocole en question, proposé par Khaled Elleyty et Abdulbast Abushgra en 2015, définit l'interaction de nos amis de longue date Alice et Bob. Leur communication se composera de plusieurs étapes interconnectées, et à un moment donné, les lecteurs seront invités à paralléliser en raison de l'utilisation de plusieurs canaux de communication différents.

Un petit programme éducatif:

Canal EPR des états intriqués

Il est basé sur le paradoxe Einstein-Podolsky-Rosen. Voici quelques liens utiles:

Première étape

Pour commencer, Alice a un texte en clair qui doit être transmis à Bob. Il doit d'abord le convertir en une représentation binaire puis en bits quantiques ( qubits ):

→ → A, A -

A = \ begin {cas} | f> = (\ alpha | 0> + \ beta | 1>), & 0 \\ | f> = (\ alpha | 0> - \ beta | 1>), & 1 \ end {cases}

, (DM)( ), , . ( ). , , . -PNS

DM, ( - , - ))

, . ( ),  Ikubit,    , (|×> |+>) . 

- , .

-

4- -

| \ Phi _ +> = \ frac {1} {\ sqrt2} (| 00> _ {AB} + | 11> _ {AB})| \ Phi _-> = \ frac {1} {\ sqrt2} (| 00> _ {AB} - | 11> _ {AB})| \ psi _ +> = \ frac {1} {\ sqrt2} (| 01> _ {AB} + | 10> _ {AB})| \ psi _-> = \ frac {1} {\ sqrt2} (| 01> _ {AB} - | 10> _ {AB})

Iepr :

string Iepr
Iepr

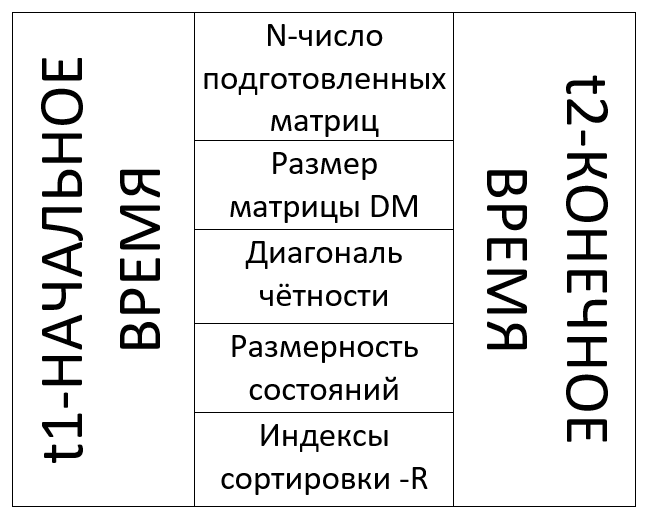
(t1,t2)- , ,  Iepr. N - ( ). DM, . p, , .S - , , . R - , .

:

-

, , - Iepr

  • ,

  • .

| \ Phi_ {ab}> \ otimes | \ varphi_c> = \ frac {1} {\ sqrt2} (| 0> _A | 0> _B + | 1> _A | 1> _B) \ otimes (\ alpha | 0> _C + \ beta | 1> _C) = \ frac {1} {\ sqrt2} (\ alpha | 000> + \ beta | 010> + \ alpha | 101> + \ beta | 111>) _ {ACB}

  • , :

| \ Phi _ {ABC}>: | \ Phi _ {AC}>, | \ phi _ {B}>

  • AC- , B- .

| \ psi_ {AC}> \ otimes (\ alpha | 0> + \ beta | 1>) _ B

,

  • , , (00,01,10 11) ( ),

( Iepr),   , . n- (SSK) n- ,  XOR. .

Iepr( ), Ikubit (|×> |+>) 4- ( ). ( ) . , Ikubit . QBERT( ), Iepr.

: Man-In-Middle(MIMA)  The Intercept-Resend Attacks. .

:

sur

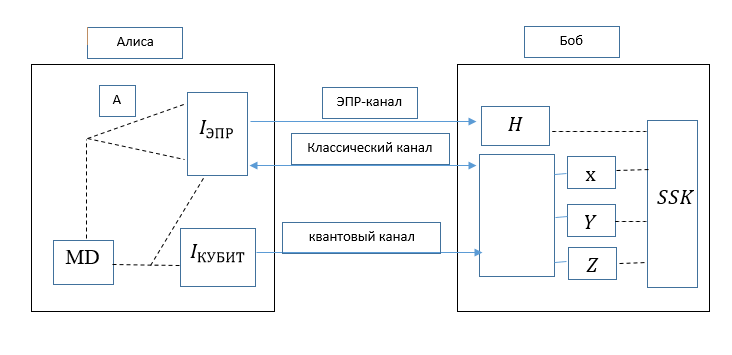
Alice et Bob lancent d'abord la communication EPR avec échange d'intrication. Si cela réussit, les deux parties commencent à échanger des qubits pour créer une clé secrète. Après avoir reçu la ligne I kubit  , Bob construit la matrice, et en utilisant la ligne avec des indices R, il restaure le bon DM. Et il effectue la première enquête en insérant une chaîne de parité dans une matrice, puis compte chaque ligne pour voir si elle est paire. S'il y a une ligne impaire, elle doit être vérifiée pour les erreurs. Si tout réussit, la clé secrète de n qubits (SSK) est générée.

Article de l'auteur



More articles:


All Articles