
Construisez un octogone convexe avec quatre angles droits.
Le fait que je donne de tels devoirs en dit probablement long sur moi en tant qu'enseignant. Je regarde les élèves essayer d'aligner les angles droits de manière cohérente. Quand ils échouent, ils essaient de s'intercaler à angle droit. À nouveau, ils les insèrent aléatoirement dans le polygone. Le cliquetis de leur cerveau pendant l' effort de réflexion est une musique aux oreilles du professeur.
Ensuite, ils deviennent méfiants et commencent à poser des questions. «Vous avez mentionné les angles droits. Peut-être vouliez-vous vraiment dire trois coins? "," Vouliez-vous vraiment dire un polygone convexe? "," Quatre angles droits, en fait, forment un rectangle. Comment pouvons-nous avoir quatre côtés de plus dans l'octogone? " J'écoute attentivement, acquiesce, confirmant leurs suppositions.
Enfin, quelqu'un pose la question que personne n'osait poser, la question que j'attendais: "Hé, est-ce encore possible?"
Cette question a le pouvoir de changer votre façon de penser en mathématiques. Ceux qui pensaient étroitement à des conditions spécifiques doivent maintenant réfléchir plus largement à la manière dont ces conditions s'articulent. Ceux qui travaillent au sein du système doivent prendre du recul et étudier le système lui-même. Tout au long de l'histoire des mathématiques, cette question a été posée à plusieurs reprises, elle a déconcerté ceux qui ont résolu le problème de la quadrature d'un cercle pour se déplacer dans la ville de Königsberg . Et cette question nous permet de formuler ce que sont les mathématiques et comment nous les comprenons.
Par exemple, trouver un octogone avec certaines propriétés est très différent de la tâche de démontrer qu'un tel octogone ne peut pas exister. En expérimentant avec différents octogones, nous pourrions en rencontrer un avec quatre angles droits.
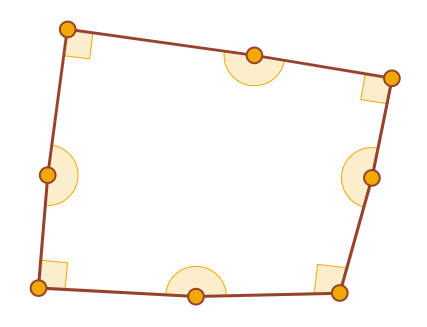
Ceci n'est pas un exemple. En fait, cet octogone n'a pas quatre angles droits.
Mais la chance ne joue aucun rôle pour prouver qu'un tel octogone ne peut exister. Cela nécessite une connaissance approfondie, non seulement des polygones, mais des mathématiques elles-mêmes. Pour rendre compte de l'impossibilité, nous devons comprendre que le simple fait de supposer l'existence d'un objet ne prouve pas son existence. Les définitions, propriétés et théorèmes mathématiques vivent sous la pression de leur interconnexion. En essayant de représenter un octogone avec quatre angles droits, nous sommes dans ces règles interdépendantes.
Mais pour réaliser qu'un octogone est impossible, nous devons prendre du recul et regarder la situation dans son ensemble. Quels principes mathématiques et géométriques peuvent être violés par un octogone à quatre angles droits? Un bon point de départ ici est la somme des angles d'un théorème de polygone.
La somme des angles intérieurs d'un polygone à n côtés est déterminée par la formule:
S = ( n - 2) × 180 °
Cela s'est produit parce que chaque polygone à n côtés peut être découpé en ( n - 2) triangles, la somme des angles intérieurs de chacun étant de 180º.
Dans le cas d'un octogone, cela signifie que la somme de ses angles intérieurs est (8 - 2) × 180º = 6 × 180º = 1080º. Ensuite, si quatre de ses angles sont droits, c'est-à-dire que chacun est de 90 °, alors c'est 4 × 90 ° = 360 ° des angles totaux. Cela signifie qu'il reste 1080º - 360º = 720º pour les quatre coins restants de l'octogone.
Cela signifie que la moyenne des quatre coins restants doit être:
Mais les angles intérieurs d'un polygone convexe doivent être inférieurs à 180 °, ce qui est impossible. Un octogone convexe à quatre angles droits ne peut pas exister.
Prouver l'impossibilité de cette manière nécessite de prendre du recul et de voir comment diverses règles mathématiques, par exemple, la formule de la somme des angles d'un polygone et la définition d'un polygone convexe, existent en pression mutuelle. Et comme les preuves d'impossibilité reposent sur un raisonnement plus large sur un ensemble de règles, il existe souvent plusieurs façons de construire une telle preuve.
Revenons à notre observation précédente selon laquelle quatre angles droits forment un rectangle.
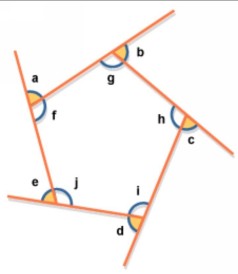
Coins extérieurs du polygone.
Si l'octogone avait quatre angles droits, en contournant uniquement ces coins, nous aurions fait un cercle complet, comme si nous avions complètement fait le tour du rectangle. Cette pensée nous conduit à une règle qui fournit encore une autre preuve d'impossibilité. On sait que la somme des angles extérieurs d'un polygone convexe est toujours de 360 °. Puisque le coin extérieur d'un angle droit est également un angle droit, nos quatre angles droits représentent les 360 ° entiers de la somme des angles extérieurs de l'octogone. Autrement dit, il ne reste plus rien pour les quatre autres coins, et nous avons de nouveau établi qu'un tel octogone est impossible.
Prouver que quelque chose est impossible est un événement mathématique puissant. Cela change notre point de vue, on passe du respect des règles aux règles de contrôle. Et pour contrôler les règles, nous devons d'abord les comprendre. Nous devons savoir non seulement comment les appliquer, mais aussi les situations dans lesquelles elles ne sont pas applicables. Et trouvez également des situations dans lesquelles les règles peuvent entrer en conflit les unes avec les autres. Dans le processus d'étude de l'octogone, nous avons identifié la relation des polygones, la convexité, les angles droits et les sommes d'angles. Et cela souligne que S = ( n - 2) × 180º n'est pas seulement une formule: c'est l'une des conditions dans le monde des conditions conflictuelles.
Les preuves d'impossibilité peuvent nous aider à mieux comprendre tous les domaines des mathématiques. À l'école, les leçons de théorie des probabilités commencent souvent par lancer de nombreuses pièces imaginaires. J'invite les élèves à créer une pièce de monnaie frauduleuse qui a tendance à apparaître face à face, ce qui a la propriété suivante: lorsque vous lancez une pièce deux fois, les résultats des deux flips sont plus susceptibles d'être différents que les mêmes. En d'autres termes, vous êtes plus susceptible de lancer la tête et la queue que la tête et la queue ou la queue et la queue.
Après expérimentation et échecs mentaux, les étudiants émettent une hypothèse intéressante: des résultats différents ne sont jamais plus probables que les mêmes. L'algèbre le révèle et souligne la symétrie sous-jacente.
Disons que la pièce est déplacée vers les têtes. Nous appellerons la probabilité d'avoir des têtesoù ... Le fait que, garantit que les têtes sont plus probables que les queues avec probabilité puisque la somme des deux probabilités doit être de 1.
Si nous lançons une pièce deux fois, la probabilité d'obtenir deux faces ou deux queues est
Ici, nous ajoutons la probabilité d'obtenir deux têtes (côté gauche) avec la probabilité d'obtenir deux queues (côté droit). En utilisant l'algèbre, nous pouvons simplifier la probabilité d'obtenir le même résultat sur les deux rouleaux:
...
Dans la mesure où, Nous savons que $, ce qui signifie que les lancers sont plus susceptibles d'avoir les mêmes résultats. En fait, on le voit même si (la pièce n'est pas frauduleuse), la probabilité des mêmes résultats est , en raison de laquelle la probabilité de résultats différents de lancers est également ... Le même résultat ne sera jamais moins probable que d'autres.
Comme dans le cas du problème des polygones, nous voyons des pressions mathématiques concurrentes à l'œuvre: changer la probabilité d'obtenir un côté de la pièce change la probabilité d'obtenir l'autre, et cette interconnexion contrôle l'espace des possibilités pour les résultats de deux lancers. Nous avons exposé cette pression en essayant d'accomplir l'impossible.
Tout domaine des mathématiques peut être soumis à de telles pressions. Essayez de trouver six entiers consécutifs qui totalisent 342, et votre persévérance vous mènera à une compréhension plus profonde de la parité. (Le fait que des entiers consécutifs deviennent alternativement pairs et impairs affecte la façon dont leurs sommes peuvent être.) Trouver un polynôme cubique avec des coefficients entiers qui a trois racines non réelles vous apprend l'importance des nombres complexes conjugués - paires de nombres complexes, produit et dont la somme est toujours réelle. Et si vous essayez d'inscrire un losange non rectangulaire dans un cercle, vous découvrirez une propriété importante des quadrilatères cycliques - les coins opposés d'un quadrilatère, dont les sommets se trouvent sur le cercle, doivent totaliser 180 degrés.
Faire face à l'impossible nous permet d'explorer les limites de nos mondes mathématiques. L'impossible en soi est une sorte de généralisation, il serait donc naturel de continuer la généralisation: un octogone ne peut pas avoir quatre angles droits, mais qu'en est-il d'un décagone? Que diriez-vous d'un polygone convexe avec n > 4 côtés? Des questions comme celles-ci se heurtent aux limites de nos mondes mathématiques et approfondissent leur compréhension.
Si nous repoussons les limites plus loin, l'impossible peut même inspirer la création de nouveaux mondes mathématiques. Pour prouver l'impossibilité de quadriller le cercle(ce problème a au moins deux mille ans), une théorie moderne des nombres transcendantaux est nécessaire, qui ne peuvent pas être les racines de polynômes entiers. Pour résoudre le problème des sept ponts de Königsberg, Euler a transformé des îles et des ponts en sommets et arêtes, donnant ainsi naissance à de vastes domaines de la théorie des graphes et de la théorie des réseaux, ainsi qu'à nombre de leurs applications. Prendre la racine carrée de −1 a conduit à un système d' arithmétique complètement nouveau . Et le logicien Kurt Gödel a changé les mathématiques pour toujours, prouvant qu'il est impossible de prouver que tout ce qui est vrai est vrai.
Alors la prochaine fois que vous rencontrez un problème de mathématiques, demandez-vous: "Est-ce possible?" Faire face à l'impossibilité peut vous donner une compréhension plus profonde de ce qui est possible. Ce faisant, vous pouvez même créer de nouveaux domaines de mathématiques.
Des exercices
1. Trouvez l'aire d'un triangle avec des côtés de longueur 46, 85 et 38.
2. Soit... Trouver un tel tout, et auquel ...
3. Trouvez un carré complet dans lequel tous ses nombres constituants appartiennent à l'ensemble {2, 3, 7, 8}.
Réponses
Réponse 1
. , , . : 85 38 46. , - .
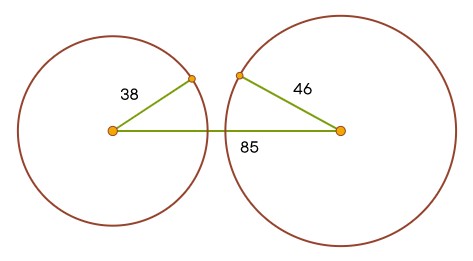
- -. !

- -. !
Réponse 2
. , , , (d) (2).
Réponse 3
, . 0, 1, 4, 5, 6 9. . 2, 3, 7 8, , .
La publicité
Quels que soient vos besoins, des serveurs abordables et fiables sont toujours les bienvenus . Même pour des calculs mathématiques complexes, la configuration maximale est de 128 cœurs de processeur, 512 Go de RAM, 4000 Go de NVMe.
