
Bonne journée!
Dans le monde moderne, il y a de plus en plus de déclarations sur la menace potentielle des ordinateurs quantiques en relation avec les protocoles de cryptographie utilisés. L'ordinateur quantique est déjà capable de résoudre les problèmes de logarithme discret et de factorisation d'un nombre, ce qui met en péril tous les protocoles basés sur eux.
Aujourd'hui, nous allons considérer le protocole NewHope, qui est basé sur une autre tâche difficile - le problème de l'apprentissage avec des erreurs dans un anneau (Ring-LWE).
NewHope – , , . , SIS, LWE Ring-LWE:
1. SIS
SIS (Short integer solution problem) – .
, n q ( ):
A:

( ) , .
, ,
. , , .
, z,
. z ( q). , , . , .
? , ( ).
- . z.
, z A .
, , n - .
2. LWE ( Learning with errors)
:
:
n – ;
q – , . n, ;
, );
;
k, .
, , s
. ( q):
.
, (LWE on lattices).
:

– .
, q. .
, , :
:
.
3.
LWE, - SIS:
Public key encryption (LWE):
, . – .

,
0, 0, 1.
?
.
, , 4 , .
One-way function (SIS):
- -:

, . . (IV).
, ,
.
- (One-way function):
, :
.
-
:
SIS.
? , SIS .
4.
:
.
15 :

2) / , .
?
5. Ring-LWE
.
? , LWE . , n ?
?
– ,
, n – .
c q.
? . , , : . .
/? , 2 ,
LWE , , .
6. NewHope
, NewHope , Bos, Castello, Naehrig Stebila. TLS Ring-LWE.
, NewHope.
, .

:
, .
n = 1024, q = 12289 ( ,
). NTT ( ), n – , q – , .
a. : seed – 256 , SHAKE-128 ( SHA3). , 1024 a. : , TLS ( 2 ), NewHope , a. , backdoor , “” .
– , . - , ( ). seed /dev/urandom 16- . s e.
( b, seed).
a, s’, e’, e”, u.
v, , . .
,
, , . , – , 0
. , .
. : . q ,
.
( ).
. .
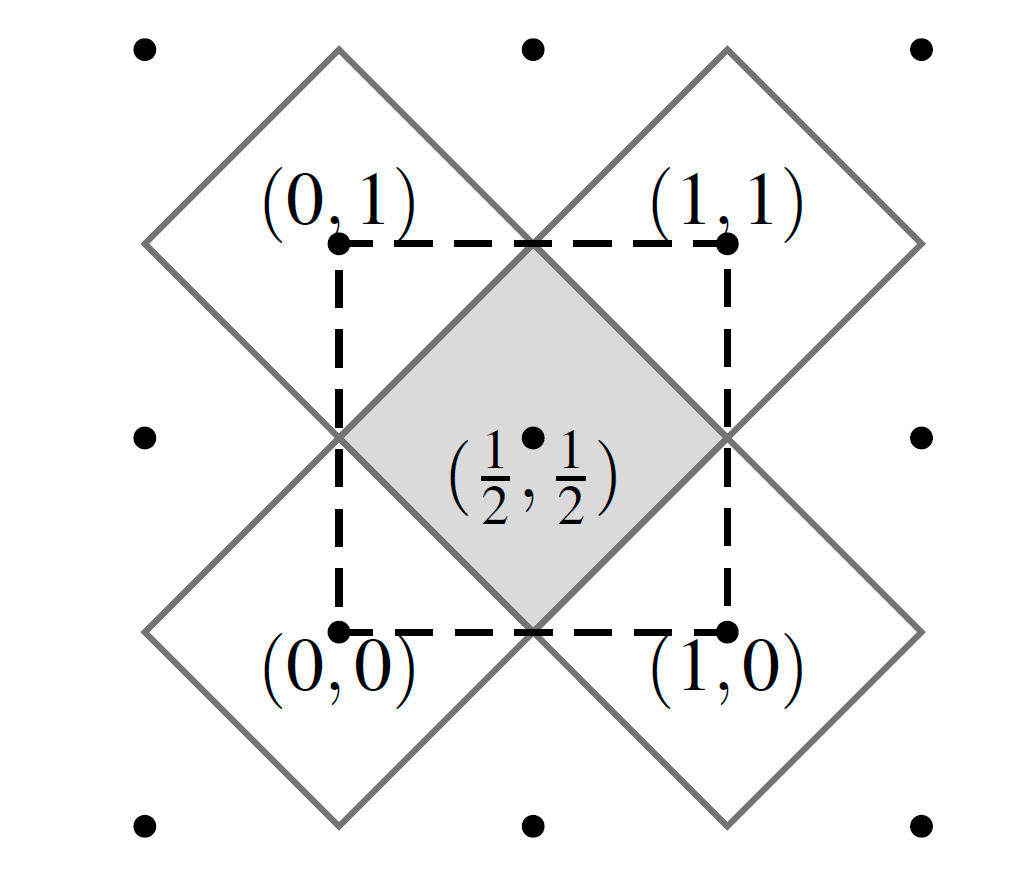
. , , : , 1, , 0. , , . HelpRec, . . , , .
8. Rec 1 4 ( ).
9. 256 , , .
7.
2019 NIST post-quantum crypto project, , . NIST , , KYBER ( Module-LWE) , . 3 KYBER.
, Google Canary CECPQ1 CECPQ2.
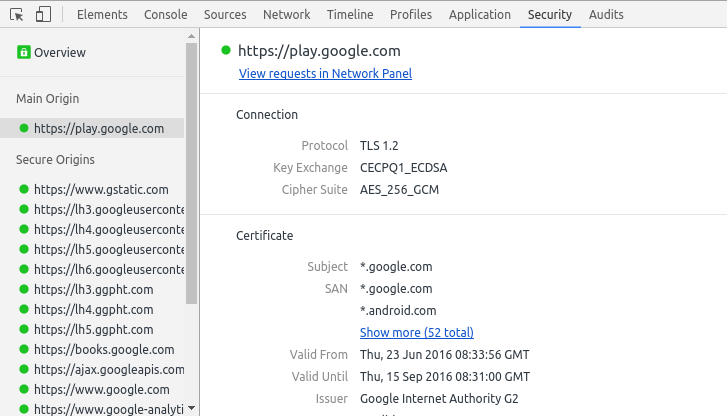
:
:
-
https://eprint.iacr.org/2015/1092.pdf
https://eprint.iacr.org/2014/599.pdf
https://www.di.ens.fr/chloe.hebant/presentation/SISproblem.pdf
http://www.ee.cityu.edu.hk/~twhk05/achieve/Wai%20Ho%20Mow.pdf
https://simons.berkeley.edu/talks/lwe-worst-case-average-case-reductions-and-cryptomania
https://simons.berkeley.edu/talks/algebraic-lattices-and-ring-lwe
https://www.ei.ruhr-uni-bochum.de/media/sh/veroeffentlichungen/2013/08/14/lwe_encrypt.pdf
-
https://people.csail.mit.edu/vinodv/6876-Fall2015/L12.pdf
https://security.googleblog.com/2016/07/experimenting-with-post-quantum.html