Olympiade mathématique. Le concours de mathématiques William Lowell Putnam est un concours de mathématiques destiné aux étudiants de premier cycle qui étudient dans des universités (collèges) aux États-Unis et au Canada. L'inspiration pour les Jeux olympiques était William Lowell Putnam, un avocat et banquier américain. Tenu par la Mathematical Association of America chaque année depuis 1938. Des prix en argent sont décernés aux cinq meilleures équipes universitaires (prix de première place de 25 000 $) et aux vingt-cinq meilleurs étudiants individuellement (prix de première place de 1 000 $).
- Wikipédia
L'Olympiade dure deux fois pendant 3 heures, 12 problèmes au total, 10 points pour chacun. La note moyenne que les élèves obtiennent est de 1 ou 2. Considérons l'un des problèmes les plus difficiles de cette Olympiade.
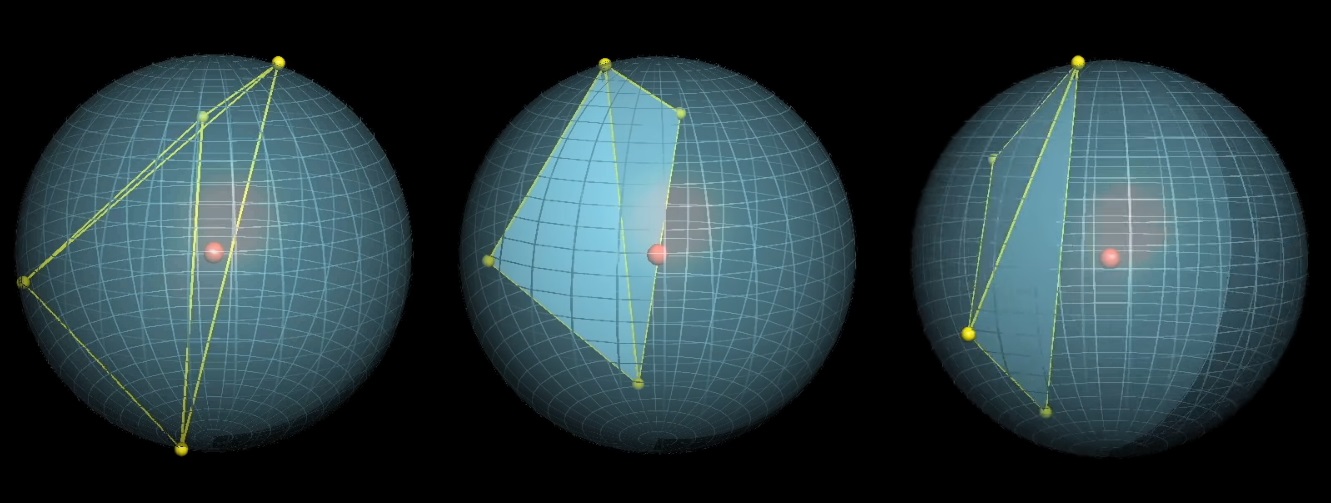
Choisissez 4 points aléatoires sur la sphère. Quelle est la probabilité que le centre de la sphère soit à l'intérieur du tétraèdre formé par ces points?
Considérons une version bidimensionnelle de ce problème.
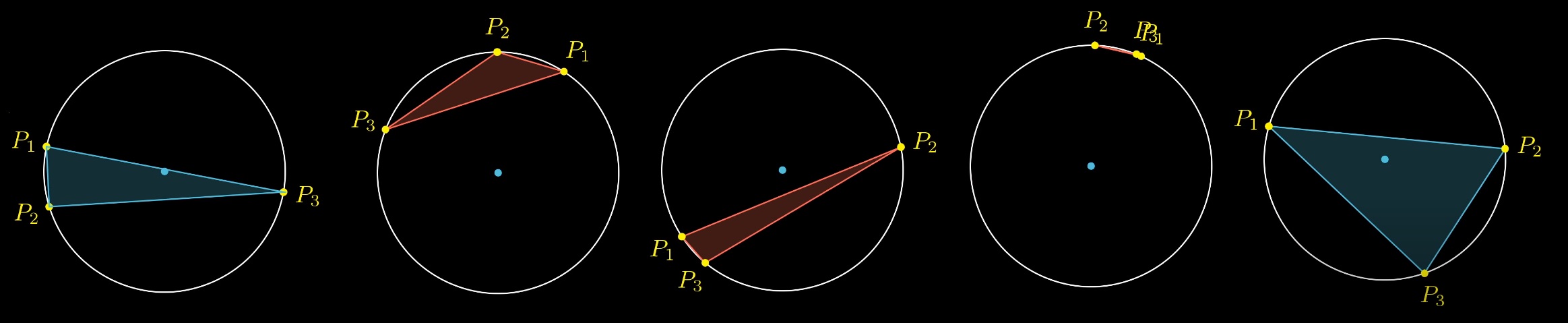
Considérez 3 points aléatoires sur un cercle. Quelle est la probabilité que le centre du cercle soit à l'intérieur du triangle?

Vous pouvez fixer deux points et jouer avec le troisième. Il est facile de voir qu'il existe une certaine zone, la projection des points ancrés par rapport au centre, à l'intérieur de laquelle le troisième point doit se situer pour que la condition soit remplie. Le cercle est ainsi divisé en 4 parties. La probabilité d'atteindre le troisième point de l'arc est égale au rapport entre la longueur de l'arc et la circonférence. Quelle est la longueur de l'arc?
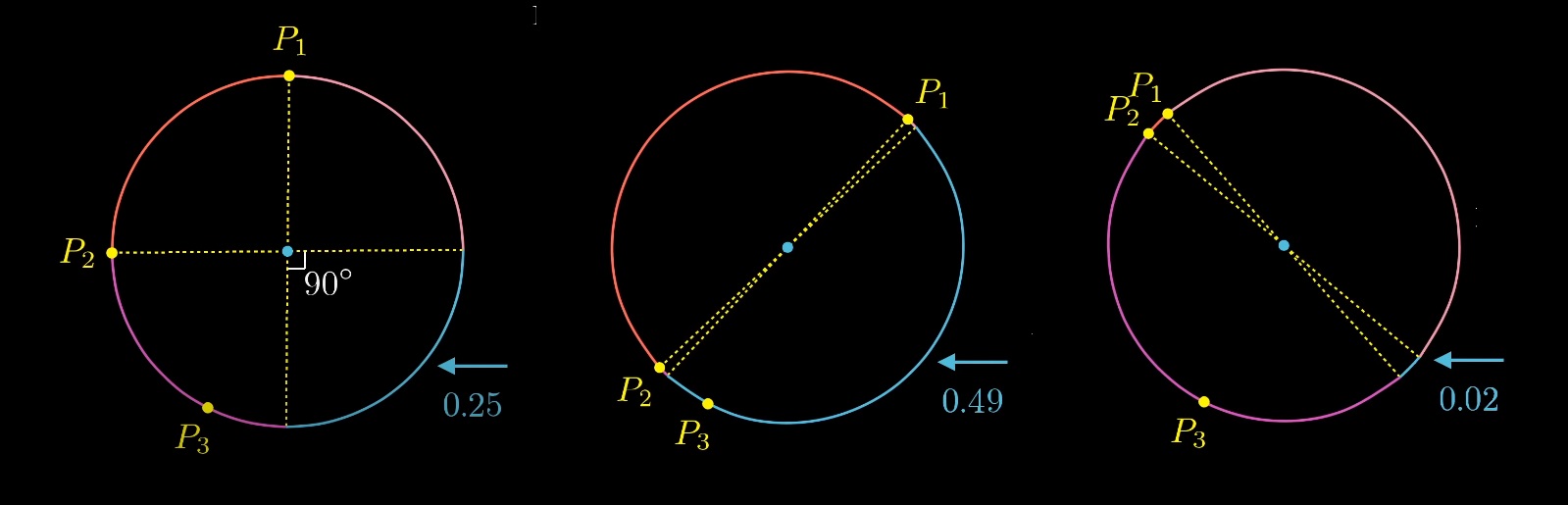
La probabilité varie de 0 à 0,5 selon l'emplacement des deux premiers points.
Quelle est la probabilité moyenne?

Fixons le premier point et jouons avec le second. La probabilité variera de 0 à 0,5, c'est-à-dire que la probabilité moyenne sera de 0,25.
Résoudre le problème pour un cercle et trois points - 25%.
Est-il possible de transférer cette approche sur une sphère et 4 points?
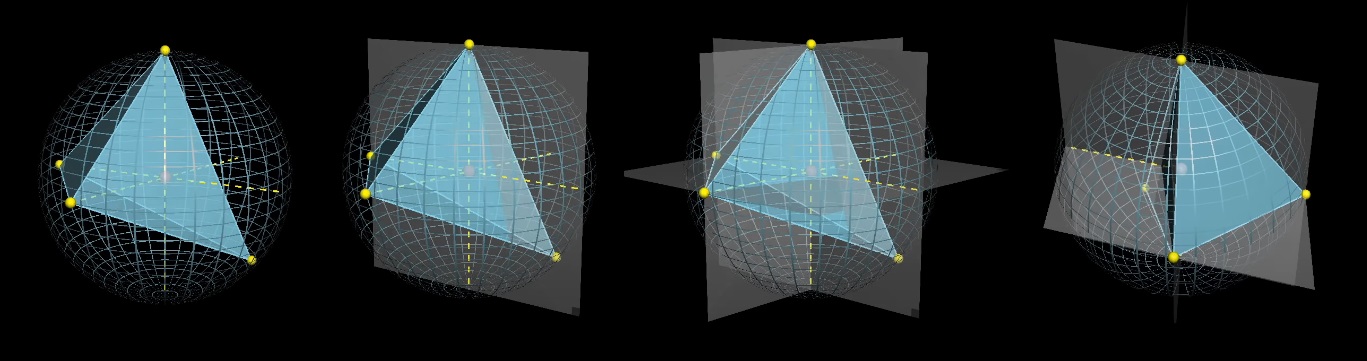
Nous fixons trois points et jouons avec le quatrième. Dessinons des projections de points fixes par rapport au centre et divisons la sphère en 8 parties avec des plans.
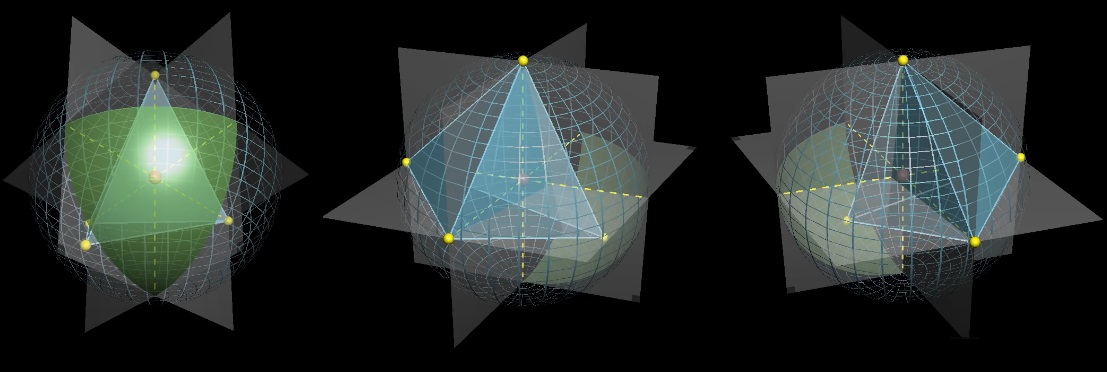
Le centre de la sphère sera à l'intérieur du tétraèdre si le quatrième point tombe sur le triangle sphérique vert, qui est "opposé" aux points fixes par rapport au centre. Quelle est la taille moyenne de la section verte?
// Ne propose rien de plus, improvise.
Vous pouvez revenir au cas à deux dimensions et réfléchir à l'origine de 1/4. D'où vient 4?
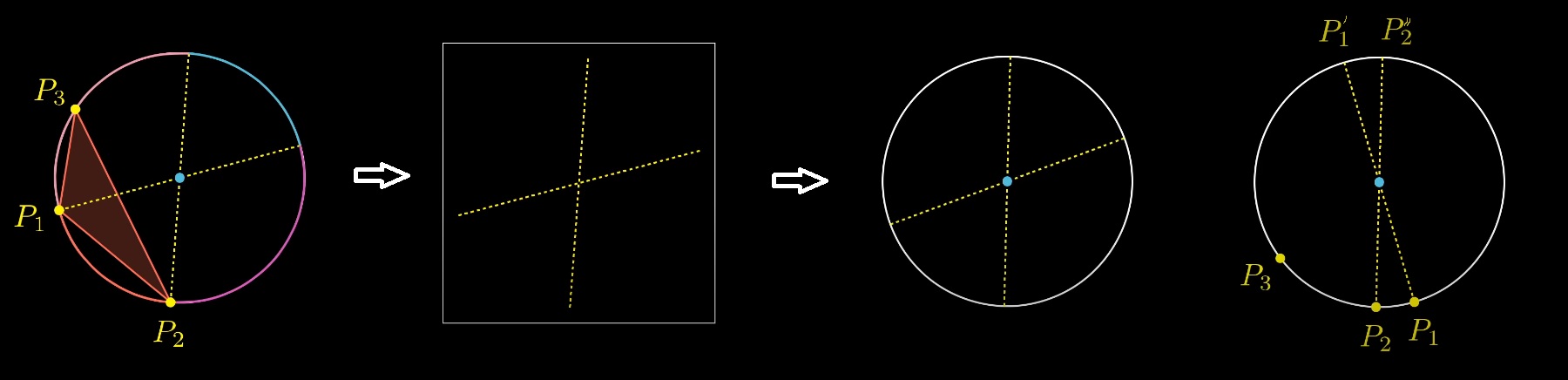
Vous pouvez passer de 3 points aléatoires sur un cercle à un autre problème. Choisissons deux diamètres aléatoires. Ensuite, pour chaque diamètre, nous lançons une pièce, choisissant ainsi où sera le point Pi, à partir de quelle extrémité du diamètre. Ensuite, nous choisissons au hasard le troisième point du cercle.
Et puis un autre coup rusé.
Commençons par sélectionner le troisième point au hasard, puis sélectionnons au hasard deux diamètres. Nous aurons 4 options pour placer les points P2 P1:
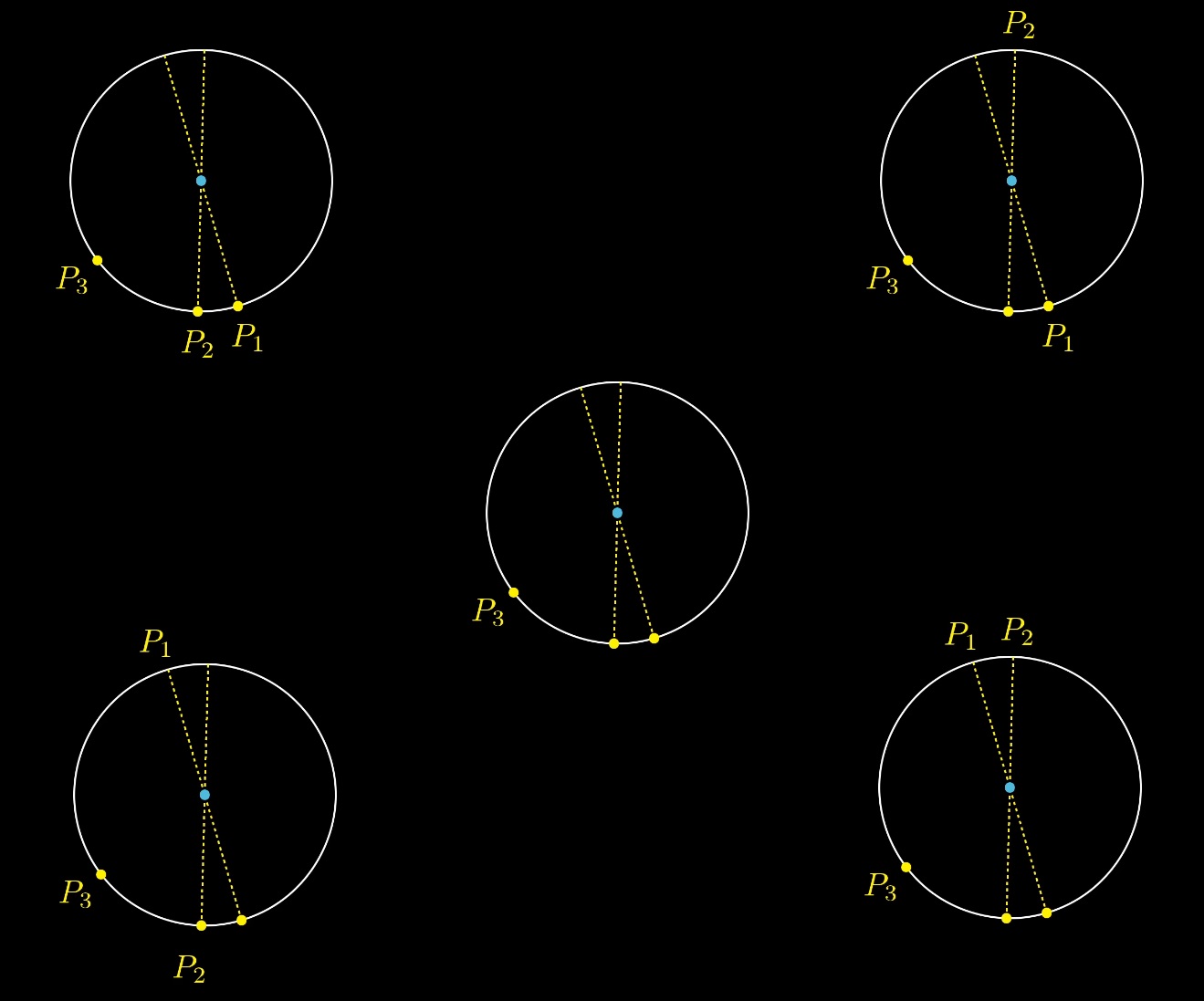
Mais une seule de ces 4 options contient une solution lorsque le centre du cercle est à l'intérieur du triangle:
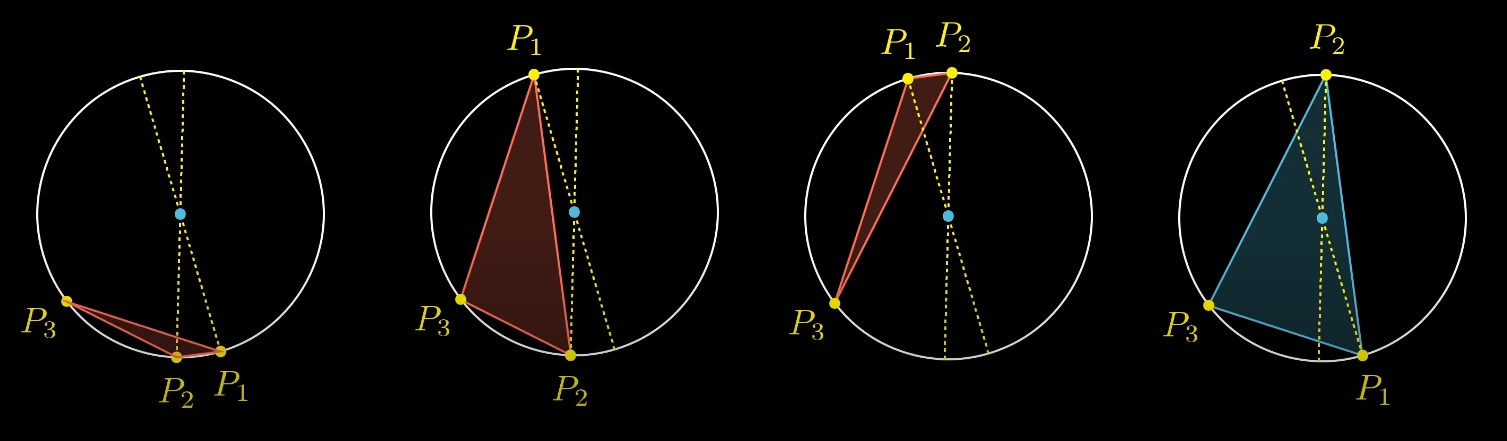
Quel que soit le choix de la position de départ aléatoire du troisième point et de deux diamètres, une seule des options contient le centre du cercle à l'intérieur du triangle:

C'est ainsi que nous avons reformulé le problème:

avec une sphère, nous obtenons 8 options pour choisir les points, après avoir fixé le premier point et choisi trois diamètres:
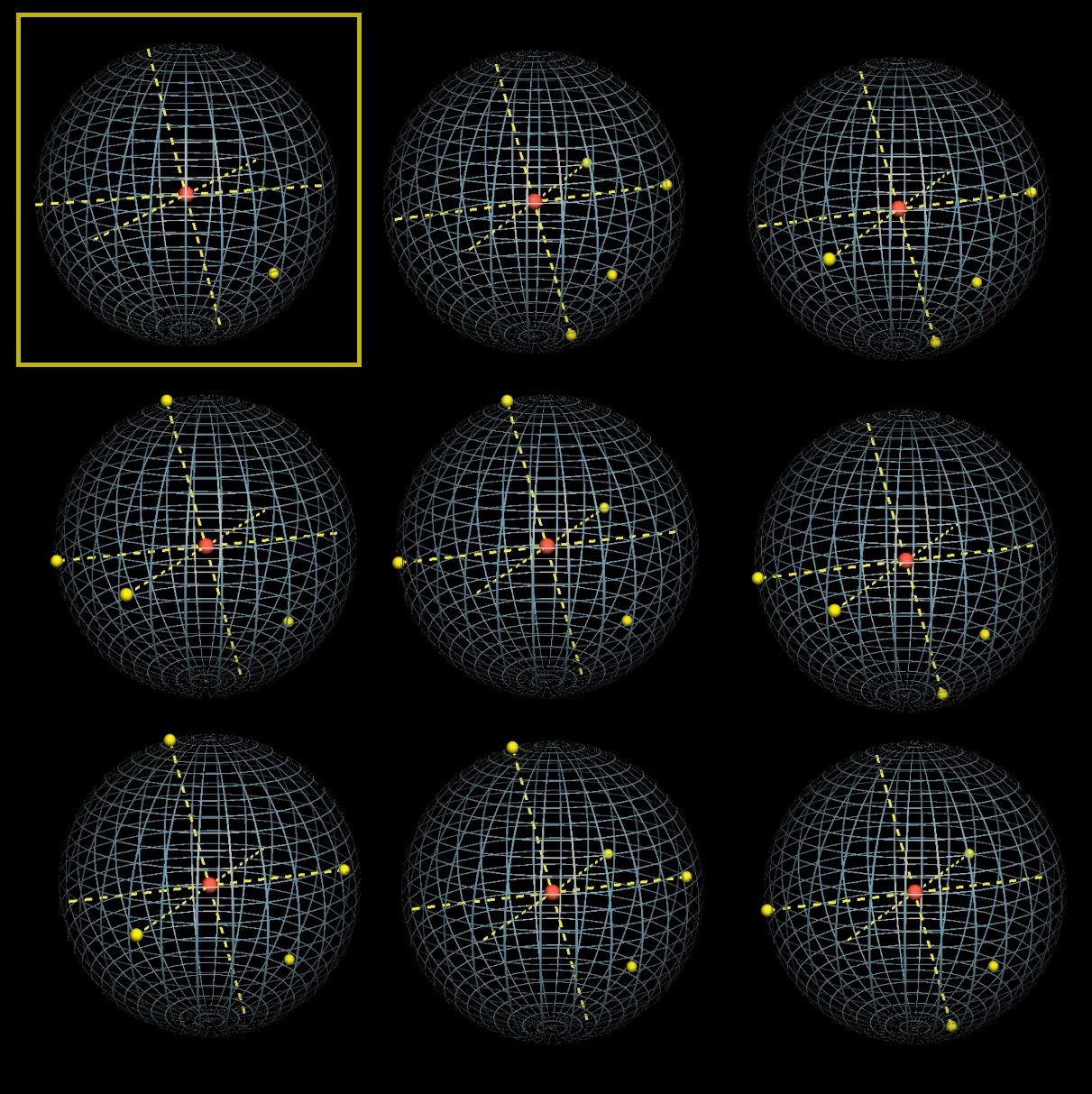
Seul 1 sur 8 satisfait à la condition que le centre de la sphère soit à l'intérieur du tétraèdre:
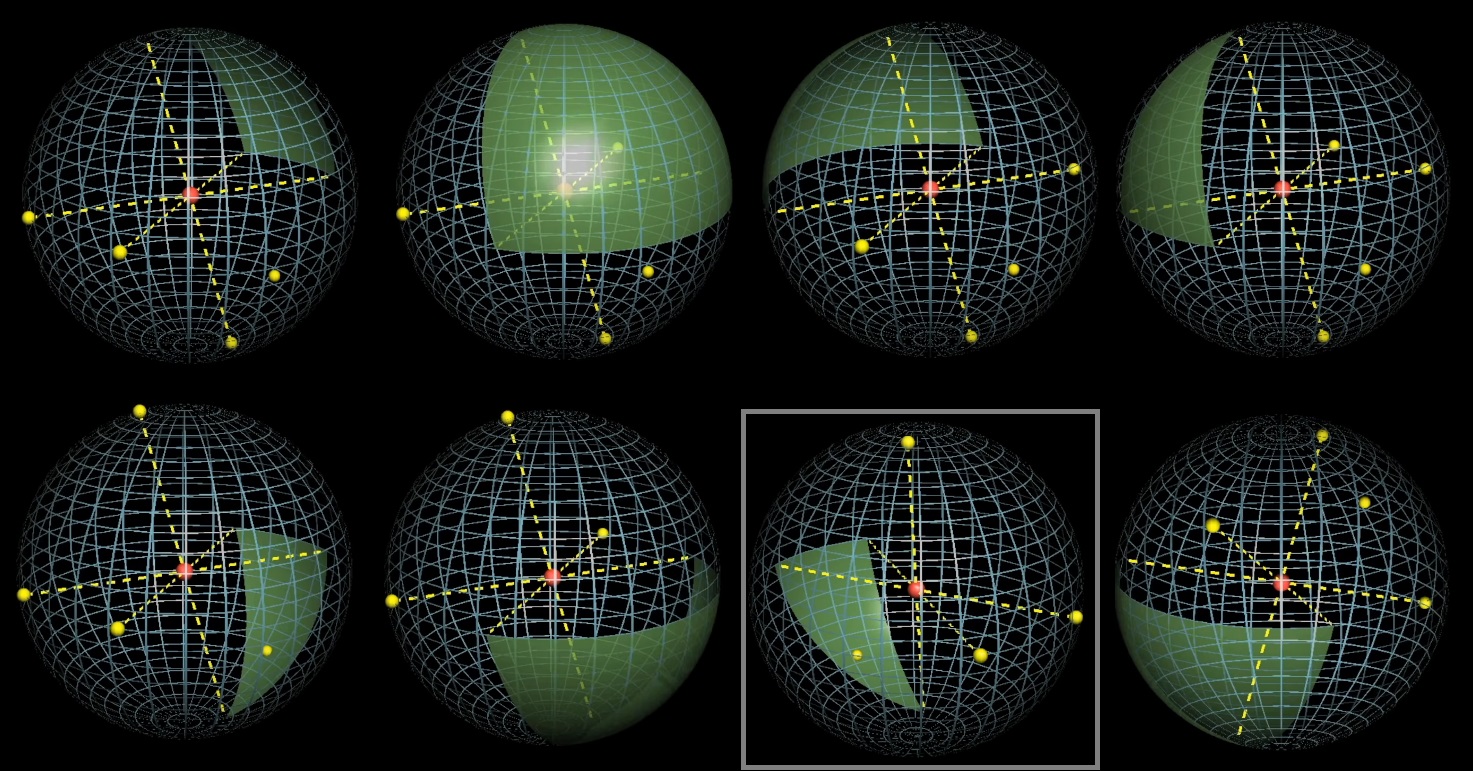
Réponse: 1/8
- L'algèbre linéaire hardcore est ici: Capturer l'origine avec des points aléatoires: généralisations d'un problème de Putnam
- Tous les problèmes de l'Olympiade de 1992: la 53e compétition mathématique William Lowell Putnam
samedi 5 décembre 1992