
J'ai participé à des exercices avec la matrice des risques de l'entreprise.
L'action s'est déroulée en trois étapes. Le premier: les garçons et les filles interrogés avec des questions comme «avez-vous arrêté de boire du cognac le matin?», Auxquelles il suffit de répondre «oui» ou «non».
À la deuxième étape, une matrice des risques «fondée sur la science» a été présentée.
Au troisième stade permanent, toutes les divisions de cette société ont essayé d'année en année de passer à des postes inférieurs sur la matrice, mais cela n'a été possible que grâce au charme personnel. Ceux qui ne pouvaient pas bouger devenaient extrêmes en cas d'échec commercial.
1. Matrice des risques: il est pratique de remplir, il n'est pas pratique de travailler.
Voici une matrice de risque typique proposée par Google.

Par exemple, une matrice de risque aléatoire d'un très ancien rapport a été trouvée sur Internet.
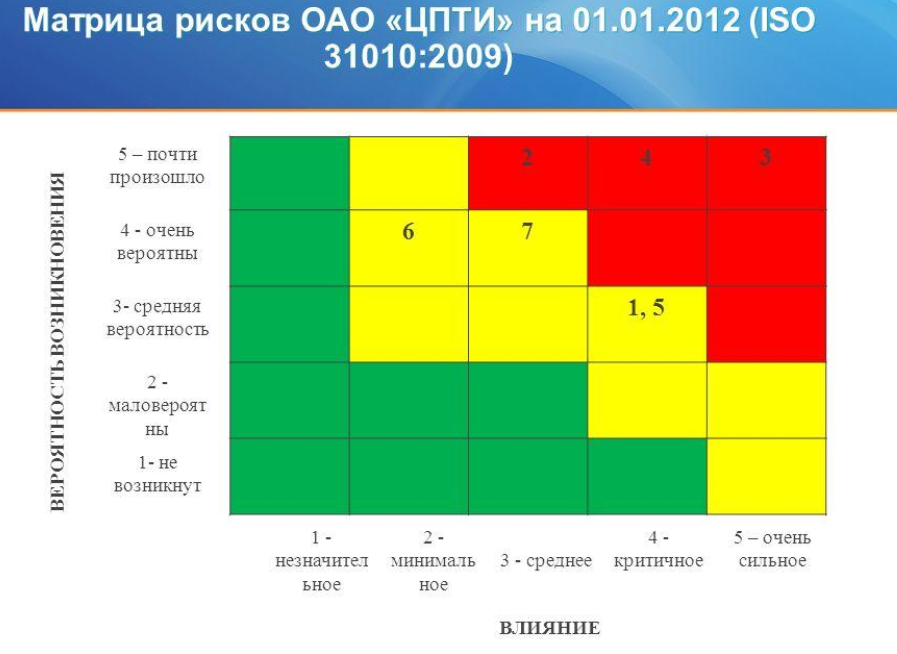
Les nombres à l'intérieur des rectangles colorés représentent des interprétations significatives des risques qui ne sont pas encore vraiment nécessaires. La description du risque est très large et vague. Il est difficile de croire que tous les éléments de la description, séparément et ensemble, donnent un numéro unique dans une plage très étroite.
Si vous suivez la matrice Google typique, toutes les descriptions significatives de «probabilité» et «impact» peuvent être associées à des nombres spécifiques.
Voici un modèle de matrice Google modernisée avec des probabilités multipliées correspondant à une mise à l'échelle horizontale et verticale.

Ce n'est pas très pratique pour appliquer des opérations matricielles standard, car il est symétrique par rapport à la diagonale supplémentaire, et non principale.
Il est possible que la matrice des risques sous cette forme soit plus pratique pour les gestionnaires. Son réarrangement symétrique autour de la diagonale principale ne change pas l'essence de la matrice. Sinon, vous pouvez toujours revenir en arrière et revenir à la vue d'origine.
La matrice est reconstruite en remplaçant l'ordre des lignes par l'inverse (symétrie autour de l'axe central vertical). En conséquence, une matrice est obtenue qui est symétrique par rapport à la diagonale principale.

Les mêmes transformations pour la matrice de risque étudiée.

Les nombres autres que 0 sont le nombre de risque associé à une certaine unité structurelle. Cet encodage n'a lieu qu'en lien avec la hiérarchie bureaucratique de l'entreprise, et non avec les risques. Par exemple, pour l'élément {1,5}. En termes de risque, la situation n'est pas différente si les descriptions de risque1 et de risque5 sont combinées. S'il s'agit de risques différents, vous pouvez réduire l'étape de la matrice et placer le risque dans une position plus appropriée.
En fin de compte, les transformations devraient faire de chaque risque différent un élément distinct.
La position [1,3] dans le système de numérotation matricielle standard signifie l'élément à l'intersection de la 1ère ligne et de la 3ème colonne. Pour la matrice considérée, en position [1,3] se trouve le nombre 2. Cela signifie que s'il y a une échelle avec la valeur maximale «5 - presque arrivé» (1.), alors en [1,3] on attend «3 - moyenne» ( 0,6) influence. Soit «l'influence» dans l'intervalle mis à l'échelle correspondre à un certain dommage: 5-d5, 4-d4, 3-d3, 2-d2,1-d1. Ensuite, si pendant une certaine période il y a eu 1 accident du groupe 2, alors les dommages seront de 1. * 0.6 * d3 * 1, et si n accidents du groupe 2 se sont produits pendant la même période, alors les dommages seront de 1. * 0.6 * d3 * n
Ensuite, la matrice étudiée prendra la forme.

Une autre transformation est effectuée: la transposition en changeant les positions des colonnes et des lignes.

La ligne du bas de la légende devient redondante, car la probabilité correspondante est prise en compte dans les valeurs de la matrice. La première colonne verticale est également prise en compte dans les valeurs de la matrice, mais elle est importante en ce qu'elle définit la structure des événements qui peuvent être enregistrés ou prédits sur une certaine période. Ayant un vecteur colonne à partir du nombre d'événements liés au type correspondant (très fort, critique, ...), vous pouvez multiplier la matrice par un vecteur colonne de manière standard et obtenir un montant structuré de dommage.
Sans la légende, la matrice ressemblera à ceci.

2. Matrice de risque: il est pratique de calculer, pas pratique à analyser.
La première tâche principale.
Après avoir reçu la matrice A, on peut procéder à la résolution du premier problème principal: avec un nombre et une qualité connus des événements qui se sont produits, calculez le montant des dommages.
Soit pendant une certaine période 2 événements «très forts» se sont produits, 3 «critiques», 1 «moyen», 5 «minimes» et 7 «insignifiants». En multipliant la matrice A par le vecteur du nombre d'événements, on obtient la structure d'endommagement.

Dommages généraux.

Vous pouvez maintenant vérifier l'exactitude des estimations, faire des ajustements, évaluer les options possibles pour réduire le montant des dommages.
Les transformations ci-dessus de la matrice originale ont été effectuées pour obtenir une procédure de calcul simple des dommages. A partir de la matrice A, vous pouvez toujours revenir sans ambiguïté à la matrice d'origine.
3. Matrice des risques: quelle théorie se cache derrière?
Pour toute matrice carrée non dégénérée, il existe une transformation linéaire biunivoque correspondant à cette matrice. Lorsqu'on regarde une matrice, il est difficile de comprendre quelle transformation linéaire est derrière elle. De plus, on ne sait pas sur quelle base la représentation matricielle est produite.
La matrice de risque est une matrice carrée et doit correspondre à une sorte de transformation linéaire. Ce fait ne dépend pas de la méthode d'obtention de la matrice et des idées mises en œuvre dans une méthode spécifique d'obtention de la matrice.
Il est important que le déterminant de la matrice ne soit pas nul. Ce sont les exigences d'une méthode qui fournit une représentation canonique d'une matrice.
De plus, il est démontré qu'il ne s'agit pas simplement d'une limitation de la méthode, mais d'une exigence qui répond aux besoins de la pratique.
La matrice de risque considérée comporte deux lignes zéro et une colonne zéro. Dans tous les cas, le déterminant de cette matrice sera égal à zéro. Vous trouverez ci-dessous un graphique montrant comment l'entreprise entend atténuer les risques.

Les flèches montrent comment les risques seront réduits. Peu importe comment c'est, il est important que dans ce cas, la nouvelle situation soit à nouveau représentée sous forme de matrice. Cette matrice correspond à une sorte de transformation linéaire. Le passage de «l'ancienne» matrice à la «nouvelle» est une matrice et une transformation linéaire.
Que signifie un déterminant différent de zéro? C'est la capacité d'aller et venir. Si le déterminant est zéro, alors le pas "en arrière" ne peut pas être effectué.
Dans le même temps, la matrice de réduction des risques est initialement associée à «l'ancienne» matrice. Autrement dit, dans l'image, vous pouvez et devez planer "d'avant en arrière", mais dans la version formalisée, vous ne pouvez pas marcher "d'avant en arrière".
Le problème suivant est lié au fait qu'un grand risque avec une faible probabilité peut être comparé au risque d'un très grand nombre de petits risques avec une faible probabilité.
Dans l'exemple ci-dessus, les 7 événements mineurs ne causent formellement aucun dommage. Il est clair que ce n’est pas le cas. L'absence de petits risques ne fait que souligner l'insuffisance de l'inexactitude de la formation de la matrice des risques.
Que le déterminant de la matrice des risques ne soit pas égal à zéro et c'est une conséquence de la continuité du travail pour réduire les risques, et non une exigence artificielle de la méthode mathématique pour les entreprises.
Il existe donc:
- une matrice de risque, qui correspond à une transformation linéaire inconnue et à une base inconnue;
- le déterminant de la matrice, qui n'est pas égal à zéro.
Ce qui peut être fait? Apportez la matrice de risque à une forme canonique avec une base orthonormée compréhensible.
Dans l' œuvre d' Alexandre Emelin, la description allégorique suivante des avantages de la forme canonique est donnée. «Supposons qu'il y ait un morceau de papier avec un mot écrit dessus. Mais c'est tellement compliqué que les mots ne peuvent être vus. Après la transformation canonique, la feuille est dépliée pour que le mot puisse être vu. Si une base orthonormée est utilisée, le morceau de papier conservera la même taille. »
Aucune des opérations et transformations décrites dans les travaux ne change l'essence des phénomènes reflétés et contenus dans la matrice des risques.
4. Matrice de risque comme construction algébrique.
La deuxième tâche principale. Représentation canonique.
Des éléments sont ajoutés à la matrice considérée afin que le déterminant ne soit pas égal à zéro. Les valeurs sont arrondies pour éviter les formules trop volumineuses.

En outre, selon le schéma standard, la matrice est réduite à la forme canonique.
Valeurs propres de la matrice des risques.

Un travail ultérieur avec des valeurs symboliques sera difficile lors de l'orthogonalisation et le résultat sera impossible à visualiser (matrices symboliques très lourdes).
Soit (par exemple) d1 = 1, d2 = 2, d3 = 5, d4 = 8, d5 = 12.
Ensuite, la matrice de risque M dans la représentation symétrique prend la forme.

On vérifie que le déterminant n'est pas égal à zéro.
Les valeurs propres sont calculées.

Une matrice de vecteurs propres est trouvée.

Il est orthogonalisé. C'est la matrice ORT des vecteurs orthonormés.

Pour vérifier, le premier vecteur (colonne) est multiplié par paires par tous les autres. Les valeurs sont différentes de zéro, mais proches de 0.

La nouvelle base contient la représentation de la transformation linéaire d'origine (définissant la matrice de risque) dans les variables z1, z2, z3, z4, z5.

Si nous négligeons les très petits termes, alors la représentation canonique de la transformation linéaire est obtenue.

De plus, les coefficients aux carrés correspondent aux valeurs propres calculées précédemment.
Nouvelle vue de la matrice des risques sur une base orthonormée.

Il s'avère une forme quadratique alternée.
5. Utilisation pratique de la représentation canonique.
Qu'en est-il de la matrice des risques originale?
Il représente une transformation linéaire inconnue.
Ses lignes sont désignées (de haut en bas) comme x1, x2, x3, x4, x5. Les lignes de la matrice des risques représentent la décomposition sur une base inconnue.
Donc
x1 = 10 * d5 * b1 + 0 * b2 + 0 * b3 + 0 * b4 + 0 * b5,
x2 = 8 * d4 * b1 + 0 * b2 + 4 * d4 * b3 + 0 * b4 + 0 * b5 , etc.
La présence d'une base orthonormée offre une liberté de mouvement entre les variables X et Z.
Dans les variables Z, la fonction de transformation linéaire dans la base orthonormée est clairement visible. Le comportement de la même transformation linéaire dans la matrice de risque d'origine n'était pas clair.
L'avantage évident de la vue canonique est la possibilité d'ajuster le type de menace. Si initialement le classement se faisait par pas de 20%, il peut maintenant être révisé en recalculant les valeurs des extrémités des plages dans une nouvelle base. Il y aura également 5 types d'événements, mais les étapes entre eux seront différentes.
Un avantage clair de la vue canonique est la possibilité d'ajuster la mise à l'échelle pour différents types d'événements (incidents). Si initialement la mise à l'échelle des événements (très forte, critique, ...) suivait un pas de 20%, elle peut désormais être revue en recalculant les valeurs des extrémités des plages dans une nouvelle base. Il y aura également 5 types d'événements (incidents), mais les étapes entre eux seront différentes.
6. Matrice des risques: La forme quadratique définit le contenu.
Les avantages pratiques décrits peuvent sembler ridicules dans le contexte des manipulations pas tout à fait simples effectuées auparavant: «le jeu ne vaut pas la chandelle».
La forme claire, directe et simple de Google Risk Matrix ne correspond pas tout à fait au contenu de la gestion des risques.
Qu'est-ce que le risque: vous comptez sur une chose, mais en fait vous en obtenez une autre.
La matrice des risques de Google est conçue de manière à ce que l'entreprise connaisse toujours clairement ses risques et s'efforce constamment de les réduire. De plus, tous les risques élevés avec des dommages importants sont progressivement éliminés. Félicitations aux sages gestionnaires.
Au contraire, la matrice de risque obtenue sur la base orthonormée montrera toujours la présence de risques élevés non vides.
La représentation canonique formée dans la section 4 peut être interprétée comme le dommage qui se produit lorsque les événements attendus se produisent: la variable dans le carré.

Il y a une autre circonstance importante. Des dommages surviennent également si des frais sont engagés pour éviter des situations qui ne se produisent pas.
Nouveau design suivant.

Les valeurs v [i, j] correspondent au dommage (bénéfice) à condition de compter sur l'événement f (j), mais l'événement f (i) s'est effectivement produit. Les valeurs v [i, j] peuvent être positives (préjudice) ou négatives (avantage).
La valeur v [i, i] correspond à une situation où l'événement pour lequel nous nous préparions s'est réellement produit: ce que nous attendions, c'est ce que nous avons obtenu.
Dans ce cas, la matrice des risques prend la forme.

Le vecteur colonne d'événements a la forme.

Dans ce cas, le montant des dommages est décrit par une forme quadratique.

La nouvelle construction présentée de la description des risques peut être associée aux calculs suivants: évaluation des dommages dans la survenance réelle de l'événement f (i), tandis que les mesures sont focalisées sur l'événement f (j).
Ensuite, il devient clair quelles «mesures d'atténuation des risques» sont nécessaires:
- pour les risques qui n'étaient pas préparés, mais qui apparaissent souvent;
- pour les risques identifiés comme élémentaires.
De plus, toutes les manipulations algébriques décrites ci-dessus deviennent non seulement appropriées, mais obligatoires.
Le problème de la minimisation des risques est réduit à la minimisation de la valeur de l'endommagement donnée par la représentation canonique de la forme quadratique de l'endommagement.
7. La matrice des risques comme outil de gestion numérique.
Dans le cas général, vous pouvez utiliser différentes méthodes pour évaluer et gérer les risques: modélisation de simulation, systèmes de mise en file d'attente, évaluation de la stabilité des schémas structurels de connexion série-parallèle de composants, etc.
Dans ce cas, le «genre» des matrices de risque et ses opportunités d'amélioration commerciale sont pris en compte.
En fait, le nouveau formulaire permet à la matrice des risques de s'éloigner du rôle d '«épouvantail» et de devenir un outil normal de gestion d'entreprise numérique. L'une des nombreuses entreprises d'aujourd'hui.
Pour cela, il est nécessaire de changer la méthodologie de calcul des dommages, en se concentrant sur des valeurs quantitatives vérifiables plutôt que sur des expertises qualitatives.