En étudiant le cours Algorithms on Strings , j'ai rencontré le problème de la construction d'un arbre de suffixes . En suivant le lien vers des documents supplémentaires, je suis tombé sur une recommandation de "voir ce merveilleux commentaire sur Stack Overflow ". Après avoir étudié et mis en œuvre selon la description gratuite donnée , l'algorithme d'Ukkonen a décidé de partager la traduction.
Voici une tentative pour décrire l'algorithme d'Ukkonen; montrant d'abord comment cela fonctionne sur une chaîne simple (c'est-à-dire que la chaîne ne contient pas de caractères en double), en s'étendant progressivement à l'algorithme complet.
Quelques déclarations préliminaires:
Ce que nous construisons est essentiellement un arbre de préfixes . Il s'agit du sommet racine, dont les arêtes en sortent vers de nouveaux sommets, et les arêtes suivantes en sortent, et ainsi de suite.
Mais , contrairement à l'arborescence des préfixes, les étiquettes de bord ne sont pas des caractères uniques, pour chaque bord, l'étiquette est une paire de nombres [de, à] - pointeurs vers des positions dans le texte. Dans ce cas, chaque arête contient une chaîne de longueur arbitraire, mais ne prend que de la mémoire O (1) (deux pointeurs)
Principe de base
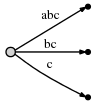
Tout d'abord, l'auteur veut montrer comment créer une arborescence de suffixes d'une chaîne extrêmement simple, des chaînes sans caractères en double:
abc
L'algorithme fonctionne par étapes, de gauche à droite . Un pas par caractère de ligne . Chaque étape peut impliquer plus d'une opération individuelle, mais nous verrons (voir les observations finales à la fin) que le nombre total d'opérations est O (n).
a
, [0, #]
- 0 . #
, , 1 ( a
).
, :
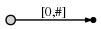
:

2 ( b
). : . :
a
-ab
b
:
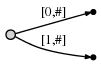
:
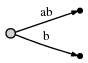
:
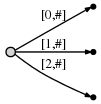
ab
, :[0, #]
. ,#
1 2.
O(1) , , , .
c
c
.
:
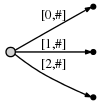
:
:
,
O(n),
#
, O(1). n, O(n)
:
, , . :
abcabxabcd
abc
, , ab
x
, abc
d
.
1 3: 3 :
4: #
4. :

a
.
, ( #
), , , , :
(_, _, _)
,
, :
abc
(, '\0x', 0)
, .._
,_
'0\x',_
. , , , .
1 . , , , 1 ( )
. a
, a
, : abca
. :
[3, #]
. ,a
. , - . , .
(, 'a', 1)
. , -a
, , 1 . ,a
. , ( , , ).
, 2
Spoiler
[4, #]
, , a
3
: , , , (
). , ( a
). , ( , O(1)), .
5: #
5. :
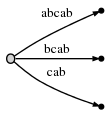
,
2, : ab
b
. - , :
a
. , ,
ab
.
b
.
, ( a
, abcab
), b
. : , b
.
, . :
(, 'a', 2)
( , ,b
)
3, , .
: ab
b
, ab
, b
. ? , ab
, ( b
) . , , , - , .
6, #
. :
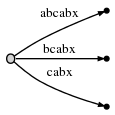
3, abx
, bx
x
. , ab
, x
. , x
, abcabx
:

- , O(1).
, abx
2. bx
. , . , , 1, , _
( 3 ).
1, :
-
_
-
_
, , ..b
-
_
1
C, (, 'b', 1)
, bcabx
, 1 , b
. O(1) , x
. , . x
, , :
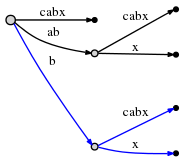
O(1),
1, (, 'x', 0)
, 1.
-. 2:
, , , , .
Spoiler
1 2
, , , , .
, . ( ):

, x
. _
0, . x
, :
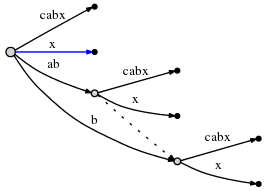
Spoiler
, .
7, #
= 7, , , a
. () , . , , (, 'a', 1)
.
Spoiler
#
, , #
8, #
= 8, b
, , , , (, 'a', 2)
, , b
. ( O(1)), . (1, '\0x', 0)
. 1
, ab
.
, #
= 9 'c', :
:
, #
c
, , , 'c'. , 'c' , (1, 'c', 1)
,
.
#
= 10
4, abcd
( 3 ), d
.
d
O(1):

_
, , .
3
_
, , , ,_
, . ,_
._
_
.
(2, 'c', 1)
, 2 :
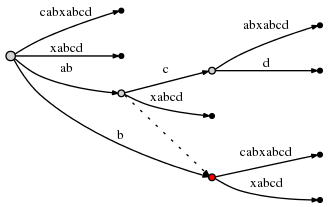
abcd
,
3 : bcd
. 3 , bcd
, d
.
, - 2 :
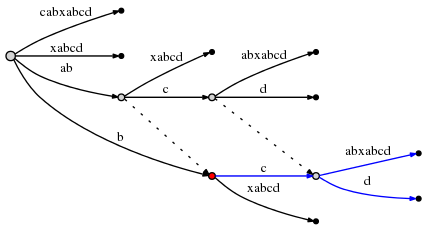
: , O(1). , , ab
b
( ), abc
bc
.
.
2, 3, . _
( ) , . (, 'c', 1)
.
, , c
: cabxabcd
, , c
. :
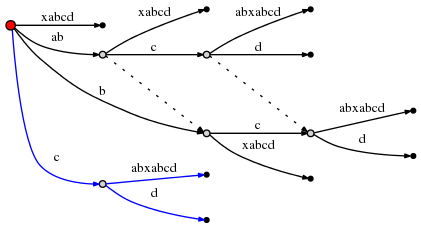
, 2 :
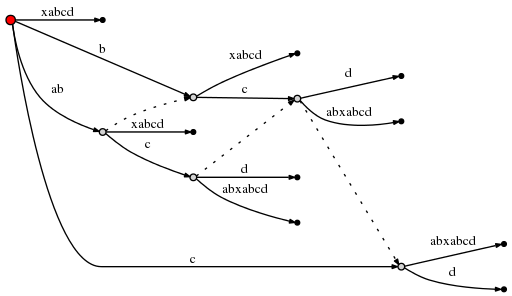
( Graphviz Dot . , , , , - )
1, _
, 1 (root, 'd', 0)
. , d
:
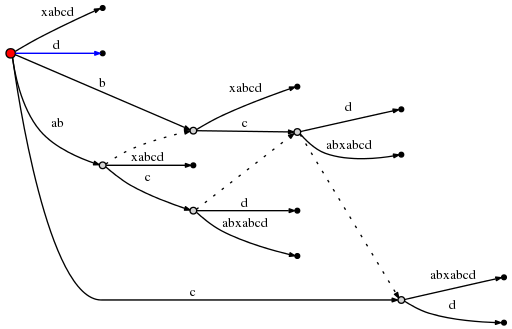
Spoiler
, . :
#
1 . O(1).
:
,
.
, . , #
. . : O(1), , , . ? ( , ).
, , , , ,
> 0. , , . , . ,
> 0, , .
Spoiler
,
> 0? , - , - . , . $
. ? → , , . , , .
- , , , . , , , .
? n , , n ( n + 1, ). ( ),
, O(1) .
, , , , , -, n ( n + 1). , O(n).
, : , , , , _
_
. , :
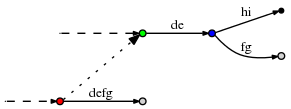
( . )
, (, 'd', 3)
, f
defg
. , , 3. (, 'd', 3)
. d
-, - de
, 2 . , , , (, 'f', 1)
.
_
,
, n. , , , , , n . , O(n2),
O(n), - _
O(n)?
. , (, , ), , , _
. , , , _
, , , , _
. _
,
,
O(n) , , -
O(n), O(n).
Notes du traducteur
En général, l'algorithme est décrit dans un langage simple et compréhensible. Suite à la description, il est possible de l'implémenter et les optimisations naturelles se feront à la volée. J'ai mis en évidence les endroits qui m'ont causé des difficultés avec les spoilers.
Dans ma mise en œuvre , l'alphabet ACGT est utilisé, car il poursuivait l'objectif de passer des tests pour un problème dans le cours.