introduction
Une fonction de hachage cryptographique est un ensemble d'étapes qui transforment un bloc arbitraire de données en une séquence de longueur fixe. Toute modification des données d'entrée entraîne une modification de la valeur de la fonction. Les fonctions de hachage permettent de calculer les sommes de contrôle, lors de la génération d'une signature électronique, lors du stockage des mots de passe dans les systèmes de sécurité sous la forme d'un code de hachage, etc.
La famille de fonctions de hachage CubeHash a été proposée comme nouvelle norme SHA-3 lors du concours de hachage du National Institute of Standards and Technology (NIST) de 2009 .
Cet article décrit le principe de fonctionnement de cette famille, et aborde également la résistance de l'algorithme à diverses attaques.
Description de l'algorithme
Ce qui suit est un algorithme de travail ![]() selon la spécification [1].
selon la spécification [1].
Le fonctionnement de l'algorithme est déterminé par 3 paramètres:
 - la taille de la séquence de sortie en bits,
- la taille de la séquence de sortie en bits, 
 - le nombre de tours,
- le nombre de tours, 
 - la taille des blocs du message d'entrée en octets,
- la taille des blocs du message d'entrée en octets, 
L'idée de l'algorithme est de transformer séquentiellement l' ![]() état en fonction de la séquence d'entrée. L'algorithme se compose de 5 étapes:
état en fonction de la séquence d'entrée. L'algorithme se compose de 5 étapes:
initialisation de l'état interne
briser un message en blocs
transformation d'état itérative
.
32 - ![]() ( little-endian).
( little-endian).
3 ![]()
![]() . .
. . ![]()
![]() .
.
. ![]() . . .
. . .
. ![]()
![]() .
. ![]()
![]() .
.
![]() 1,
1, ![]()
![]() .
.
![]() .
.
F
![]() , , , .
, , , . ![]() 10 :
10 :



 ,
, 

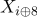 ,
, 
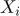
 ,
, 

 ,
, 
1
 ,
, 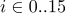

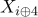 ,
, 
4

 ,
, 
![]() [2]:
[2]:

-
:
: - .
: 2 .
-, , - , , , .
CubeHash
, . .. , , .
50% ![]() . . , 128 [3].
. . , 128 [3].
. . , . ![]() . , 64 [3].
. , 64 [3].
![]() .
.
[4] , ![]() ,
, ![]() .
.
![]()
![]() .
. ![]() ( ),
( ), ![]() .
. ![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]() , .
, .
, , , ![]() . ,
. , ![]() ,
, ![]() , [2]. , , ,
, [2]. , , , ![]() .
.
F
![]() 128- [2]. 15
128- [2]. 15 ![]() :
:
|
AABBCCDD |
EEFFGGHH |
IIJJKKLL |
MMNNOOPP |
|
ABABCDCD |
EFEFGHGH |
IJIJKLKL |
MNMNOPOP |
|
ABBACDDC |
EFFEGHHG |
IJJIKLLK |
MNNMOPPO |
|
ABCDABCD |
EFGHEFGH |
IJKLIJKL |
MNOPMNOP |
|
ABCDBADC |
EFGHFEHG |
IJKLJILK |
MNOPNMPO |
|
ABCDCDAB |
EFGHGHEF |
IJKLKLIJ |
MNOPOPMN |
|
ABCDDCBA |
EFGHHGFE |
IJKLLKJI |
MNOPPONM |
|
ABCDEFGH |
ABCDEFGH |
IJKLMNOP |
IJKLMNOP |
|
ABCDEFGH |
BADCFEHG |
IJKLMNOP |
JILKNMPO |
|
ABCDEFGH |
CDABGHEF |
IJKLMNOP |
KLIJOPMN |
|
ABCDEFGH |
DCBAHGFE |
IJKLMNOP |
LKJIPONM |
|
ABCDEFGH |
EFGHABCD |
IJKLMNOP |
MNOPIJKL |
|
ABCDEFGH |
FEHGBADC |
IJKLMNOP |
NMPOJILK |
|
ABCDEFGH |
GHEFCDAB |
IJKLMNOP |
OPMNKLIJ |
|
ABCDEFGH |
HGFEDCBA |
IJKLMNOP |
PONMLKJI |
32- . . , ![]() , , . , .
, , . , .
.
( )
,
.
,
, . .
.
(cycle per byte cpb). , 1 .
SHA-256, SHA-512 CubeHash16/32 Intel Core 2Duo 6f6 (a) Intel Core 2 Duo E8400 1067a (b) [5]:
11.47 cpb: CubeHash 16/32, (b), amd64 architecture.
12.60 cpb: SHA-512, (b), amd64 architecture.
12.60 cpb: SHA-512, (a), amd64 architecture.
12.66 cpb: CubeHash 16/32, (a), amd64 architecture.
12.74 cpb: CubeHash 16/32, (b), x86 architecture.
14.07 cpb: CubeHash 16/32, (a), x86 architecture.
15.43 cpb: SHA-256, (b) x86 architecture.
15.53 cpb: SHA-256, (b), amd64 architecture.
15.56 cpb: SHA-256, (a), amd64 architecture
17.76 cpb: SHA-512, (b), x86 architecture.
20.00 cpb: SHA-512, (a), x86 architecture
22.76 cpb: SHA-256, (a), x86 architecture
CubeHash SHA-3 -, NIST. Cubehash , . , CubeHash , .
![]()
![]() . , CubeHash 8 / 1-512 CubeHash 1 / 1-512, CubeHash 1 / 1-512 , CubeHash 1 / 2-512. - CubeHash 1/128- h.
. , CubeHash 8 / 1-512 CubeHash 1 / 1-512, CubeHash 1 / 1-512 , CubeHash 1 / 2-512. - CubeHash 1/128- h.
: ![]()
![]() .
.
DJ Bernstein. Spécification Cubehash (2.b.1)
Vikash Jha. Cryptanalyse de Cubehash.
Philip Doughty Jr. Une attaque générique sur CubeHash, un candidat SHA-3.
Benjamin Bloom et Alan Kaminsky. Attaques par bloc unique et tests statistiques sur CubeHash.
DJ Bernstein. Réglage des paramètres CubeHash: 16 fois plus rapide.