Une fonction de hachage est une fonction qui convertit une longueur arbitraire de données d'entrée en une séquence de bits d'une longueur fixe. Les fonctions de hachage jouent un rôle important dans la cryptographie moderne. Les progrès technologiques, de nouvelles exigences en matière de sécurité et de complexité informatique émergent. La famille d'algorithmes SHA reste le leader parmi les algorithmes de hachage dans de nombreux domaines, mais il existe une autre famille d'algorithmes basés sur des automates cellulaires qui mérite l'attention de tous.
Automates cellulaires
L'automate cellulaire est une chose assez courante qui mérite un poste séparé . Cependant, en un mot, il s'agit d'un modèle discret, qui est une grille de dimensions arbitraires, dont chaque cellule à chaque instant du temps peut prendre l'un d'un ensemble fini d'états, et la règle de transition des cellules d'un état à un autre est déterminée.
Dans le cas des automates cellulaires élémentaires, les grilles de cellules sont unidimensionnelles.

Dans un automate cellulaire, pour chaque cellule, il existe un ensemble d'autres cellules, appelées voisinage, qui déterminent l'état suivant de la cellule. L'état initial est l'état dans lequel les valeurs des cellules et leurs voisinages sont déterminés au temps t. Désormais, une nouvelle génération de cellules est créée lorsque "t" est incrémenté de 1.
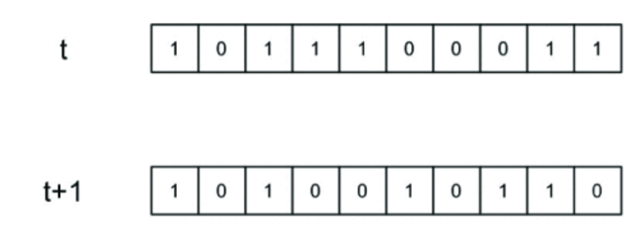
30, :
:

, .
( ).
.
.
?
, : 128, 192 256 .
:
.
.
.
512 .
512 , 8 64 .
512 30.
5 512 ().
XOR 5 512 .
, 1.
6, 7 8 , 512 , .
, .
, .
64 .
,
,
,
,
1.
,
4.
ROTL — , ROTR — .
. :
'1' (512 )
'0' (512 )
.
30 , - . . , .
:
-
Building Secure and Fast Cryptographic Hash Functions Using Programmable Cellular Automata
LCASE: Lightweight Cellular Automata-based Symmetric-key Encryption
Cellular Automata Based Hashing Algorithm (CABHA) for Strong Cryptographic Hash Function
-