Dans cet article, vous apprendrez
Qui est votre chiffrement par bloc.
À quels principes les créateurs de l'algorithme ont-ils adhéré?
À quoi ressemble le processus de préparation des clés?
Algorithme de travail.
Et qu'est-ce que RC5 a à voir avec cela?
Introduction à RC6.
RC6 ( Rivest's Cipher 6 ) est un chiffrement par blocs symétriques basé sur le réseau Festel , développé par Ronald Rivest en 1998.
Tout d'abord, voyons la terminologie:
Que signifie symétrique?
Il existe deux types de chiffrement personnes :
Symétrique (ce dont nous avons besoin)
Asymétrique (une autre fois, frérot)
Dans le cryptage symétrique , la même clé est utilisée pour crypter et décrypter les données . Cela doit être gardé secret . Ceux. ni l'expéditeur ni le destinataire ne doivent le montrer à qui que ce soit. Sinon, vos données peuvent être interceptées / modifiées ou pire encore.
Algorithmes de chiffrement symétriques:
AES (norme de cryptage avancée)
3DES (algorithme de cryptage triple des données)
RC4, RC5, RC6 (chiffre Rivest)
Dans le cryptage asymétrique utilise deux clés: publique et privée. D'après les noms, il est clair que la clé publique peut être librement transférée via les canaux de communication, mais la clé privée doit être gardée secrète.
:
RSA (Rivest-Shamir-Adleman)
DSA (Digital Signature Algorithm), DSS (Digital Signature Standard)
Diffie-Hellman
?
. , : , .
, : .
, ?
. . . .
. , .
:
— .
.
2 ( xor)
.
.
( ) .
() .
- ( ).
, .
. , , , .
:

, , .
RC6 . , , .
:
, , . , RC6
. 4 A, B, C, D
.
.
.
, . :
.
.
(.. 4 ).
.
( ).
.
.
:
.
, .
:
:
(),
( ).
.
, , :
. :
1 .
,
,
.
,
:
# x<<<y -
c = [max(b, 1) / u]
for b - 1 downto 0 do
L[i/u] = (L[i/u]<<<8) + K[i]
2 .
. , :
S[0] = P_w
for i = 1 to 2r + 3 do
S[i] = S[i - 1] + Q_w
3 .
, , :
# : b ,
# L[0,...,c-1]
# r
# : w- S[0,...,2r+3]
A = B = i = j = 0
v = 3 * max(c, 2r + 4)
for s = 1 to v do
{
A = S[i] = (S[i] + A + B)<<<3
B = L[j] = (L[j] + A + B)<<<(A + B)
i = (i + 1)mod(2r + 4)
j = (j + 1)mod(c)
}
, RC6. , , RC5. , RC6:
RC5
RC5 , 1994 . RC6
, .
.
, :
RC5 . .. () , .
RC5 , .
RC5 . , 64- , RC5 .
RC5 . .. , .
RC5 . .
RC5 . .
RC5 .
,
RC5 .
RC5 , RC6. . C RC5:
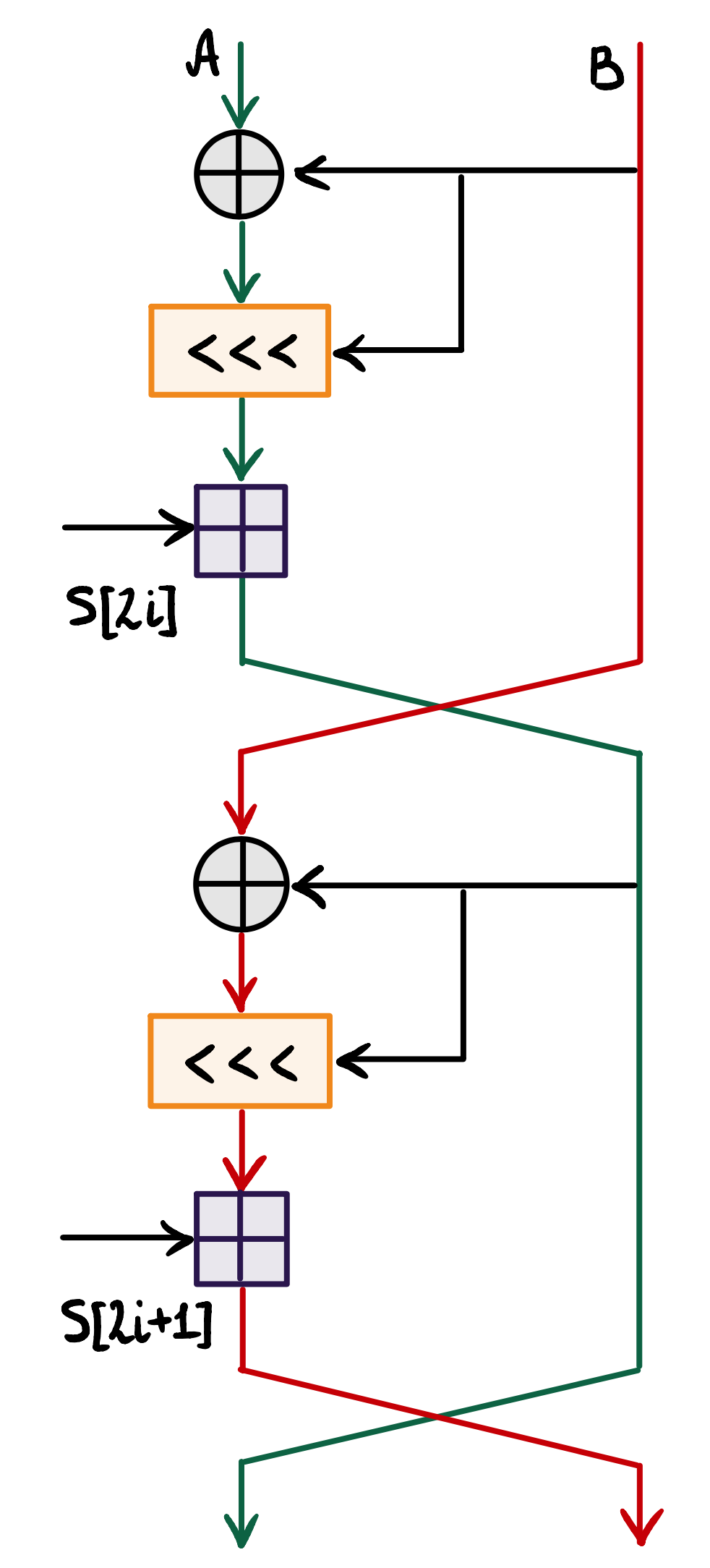
:
A = A + S[0]
B = B + S[1]
for i = 1 to r do
A = ((A xor B)<<<B) + S[2i]
B = ((B xor A)<<<A) + S[2i + 1]
, RC5 .
RC5 RC6
RC5 :
, RC6.
-( ) RC5:
for i = 1 to r do
{
A = ((A xor B)<<<B) + S[2i]
(A, B) = (B, A)
}
RC5. A B, C D:
for i = 1 to r do
{
A = ((A xor B)<<<B) + S[2i]
C = ((C xor D)<<<D) + S[2i + 1]
(A, B) = (B, A)
(C, D) = (D, C)
}
, A B C D, (A, B, C, D) = (B, C, D, A). AB CD:
for i = 1 to r do
{
A = ((A xor B)<<<B) + S[2i]
C = ((C xor D)<<<D) + S[2i + 1]
(A, B, C, D) = (B, A, D, C)
}
AB CD :
for i = 1 to r do
{
A = ((A xor B)<<<D) + S[2i]
C = ((C xor D)<<<B) + S[2i + 1]
(A, B, C, D) = (B, A, D, C)
}
, B D, , . , , .
, :
for i = 1 to r do
{
t = (B * (2B + 1))<<<5
u = (D * (2D + 1))<<<5
A = ((A xor t)<<<u) + S[2i]
C = ((C xor u)<<<t) + S[2i + 1]
(A, B, C, D) = (B, C, D, A)
}
, , ( , pre- post-whitening):
B = B + S[0]
D = D + S[1]
for i = 1 to r do
{
t = (B * (2B + 1))<<<5
u = (D * (2D + 1))<<<5
A = ((A xor t)<<<u) + S[2i]
C = ((C xor u)<<<t) + S[2i + 1]
(A, B, C, D) = (B, C, D, A)
}
A = A + S[2r + 2]
C = C + S[2r + 3]
, , , :
, RC6 A, B, C, D. , . A, D. :
# : 4- w- A, B, C, D
# r
# w- S[0,...,2r+3]
# : , A, B, C, D
B = B + S[0]
D = D + S[1]
for i = 1 to r do
{
t = (B * (2B + 1))<<<lg(w)
u = (D * (2D + 1))<<<lg(w)
A = ((A xor t)<<<u) + S[2i]
C = ((C xor u)<<<t) + S[2i + 1]
(A, B, C, D) = (B, C, D, A)
}
A = A + S[2r + 2]
C = C + S[2r + 3]
# (A, B, C, D) = (B, C, D, A) .
RC6 :
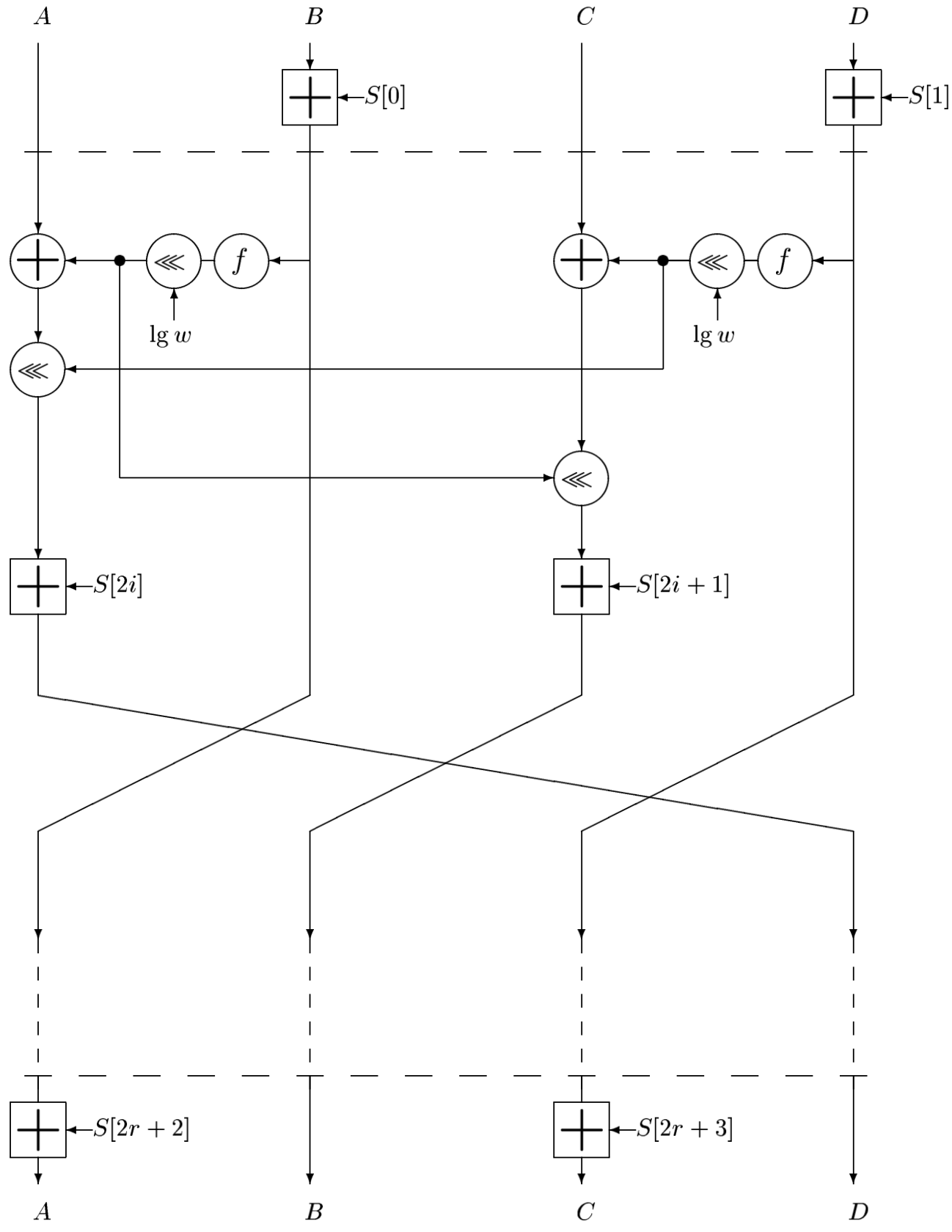
:
# : 4- w- A, B, C, D
# r
# w- S[0,...,2r+3]
# : , A, B, C, D
C = C - S[2r + 3]
A = A - S[2r +2]
for i = r downto 1 do
{
(A, B, C, D) = (D, A, B, C)
u = (D * (2D + 1))<<<lg(w)
t = (B * (2B + 1)) << lg(w)
C = ((C - S[2i + 1)>>>t) xor u
A = ((A - S[2i])>>>u) xor t
}
D = D - S[1]
B = B - S[0]
?
RC6-128/20/b .
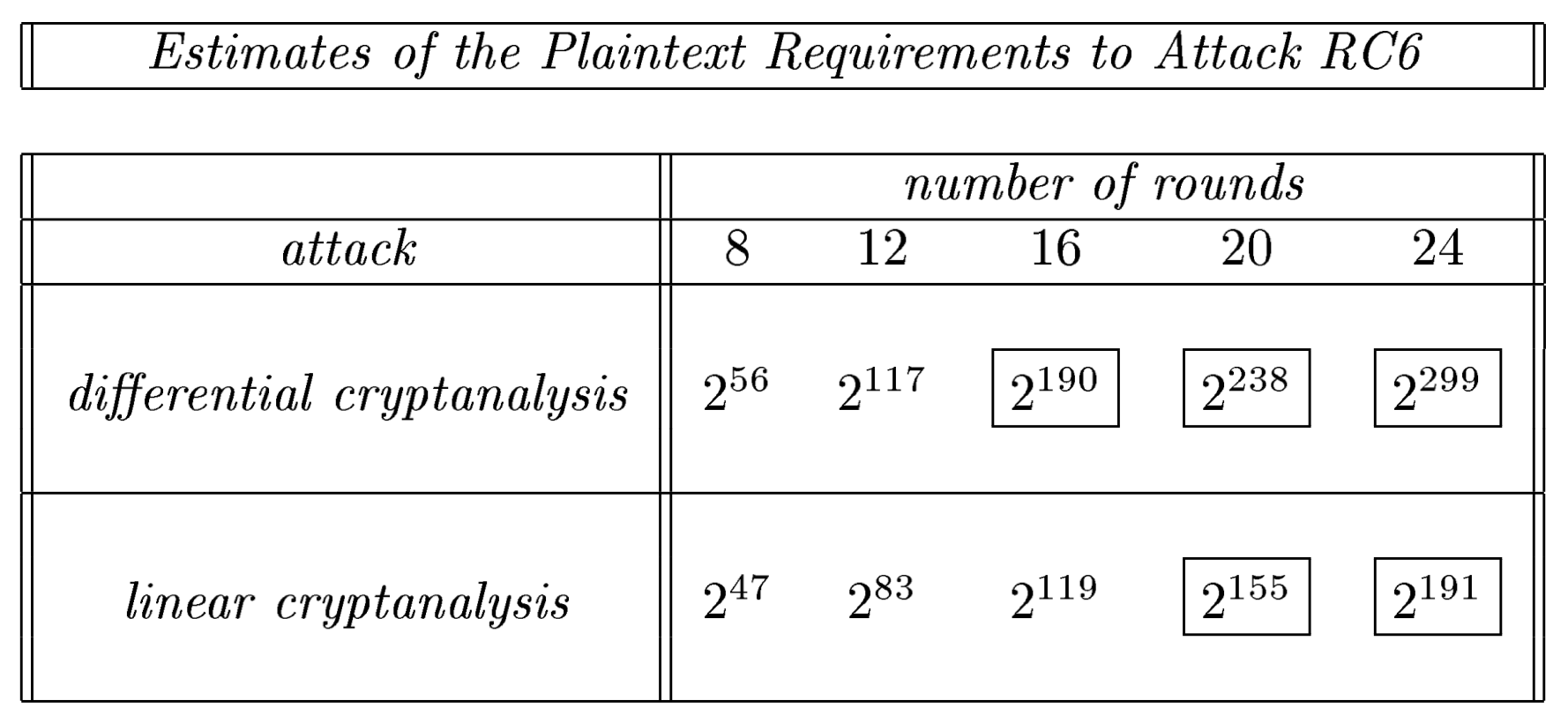
. , .
, , RC6 20 .
RC6 - , . : , . , .
RC6, RC6_en, - .
R.L. Rivest (1994) The RC5 Encryption Algorithm
RL Rivest, MJB Robshaw, R Sidney et YL Yin. (1998) Le chiffrement par bloc RC6
S. Contini, RL Rivest, MJB Robshaw et YL Yin. (1998) La sécurité du RC6