Arbre à évaser. Chercher

Bonjour, Habr! Nous invitons les futurs étudiants du cours "Algorithmes et structures de données" à un webinaire ouvert sur le thème "Réserves d'arbres de recherche binaires".



Et maintenant, nous partageons avec vous la traduction traditionnelle de documents utiles.

---

, , , (Binary Search Tree) O(n). , . O(log n) - -.

, , - -?

- -, Splay- ( ) . splay- , , , , , O(1) . , ( 80% 20% ). , , , .

splay- O(log n), n - . (n).

 

splay- , ( — splay). , . , NULL.

:

1. . , , , , .

2. Zig: ( ). ( ), ( ).

T1, T2 T3 — y () x ()

3. , . :

) Zig-Zig Zag-Zag. , ( ) , ( ).

) Zig-Zag Zag-Zig. , ( ) , ( ).

:

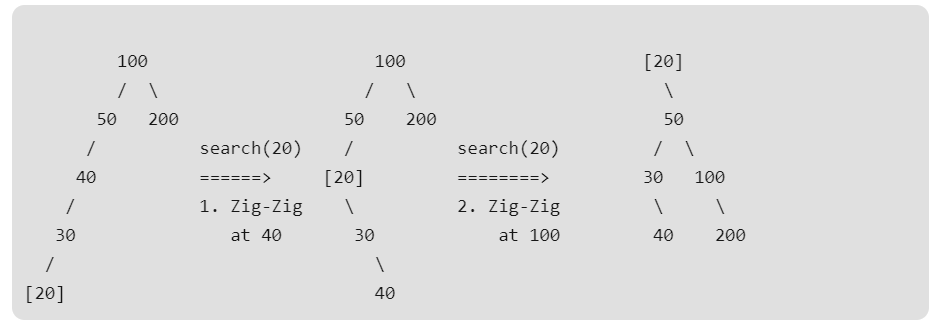
, (splay) , . , 1.

:

C++

#include <bits/stdc++.h> 
using namespace std; 

// An AVL tree node 
class node 
{ 
	public: 
	int key; 
	node *left, *right; 
}; 

/* Helper function that allocates 
a new node with the given key and 
	NULL left and right pointers. */
node* newNode(int key) 
{ 
	node* Node = new node(); 
	Node->key = key; 
	Node->left = Node->right = NULL; 
	return (Node); 
} 

// A utility function to right 
// rotate subtree rooted with y 
// See the diagram given above. 
node *rightRotate(node *x) 
{ 
	node *y = x->left; 
	x->left = y->right; 
	y->right = x; 
	return y; 
} 

// A utility function to left 
// rotate subtree rooted with x 
// See the diagram given above. 
node *leftRotate(node *x) 
{ 
	node *y = x->right; 
	x->right = y->left; 
	y->left = x; 
	return y; 
} 

// This function brings the key at 
// root if key is present in tree. 
// If key is not present, then it 
// brings the last accessed item at 
// root. This function modifies the 
// tree and returns the new root 
node *splay(node *root, int key) 
{ 
	// Base cases: root is NULL or 
	// key is present at root 
	if (root == NULL || root->key == key) 
		return root; 

	// Key lies in left subtree 
	if (root->key > key) 
	{ 
		// Key is not in tree, we are done 
		if (root->left == NULL) return root; 

		// Zig-Zig (Left Left) 
		if (root->left->key > key) 
		{ 
			// First recursively bring the 
			// key as root of left-left 
			root->left->left = splay(root->left->left, key); 

			// Do first rotation for root, 
			// second rotation is done after else 
			root = rightRotate(root); 
		} 
		else if (root->left->key < key) // Zig-Zag (Left Right) 
		{ 
			// First recursively bring 
			// the key as root of left-right 
			root->left->right = splay(root->left->right, key); 

			// Do first rotation for root->left 
			if (root->left->right != NULL) 
				root->left = leftRotate(root->left); 
		} 

		// Do second rotation for root 
		return (root->left == NULL)? root: rightRotate(root); 
	} 
	else // Key lies in right subtree 
	{ 
		// Key is not in tree, we are done 
		if (root->right == NULL) return root; 

		// Zag-Zig (Right Left) 
		if (root->right->key > key) 
		{ 
			// Bring the key as root of right-left 
			root->right->left = splay(root->right->left, key); 

			// Do first rotation for root->right 
			if (root->right->left != NULL) 
				root->right = rightRotate(root->right); 
		} 
		else if (root->right->key < key)// Zag-Zag (Right Right) 
		{ 
			// Bring the key as root of 
			// right-right and do first rotation 
			root->right->right = splay(root->right->right, key); 
			root = leftRotate(root); 
		} 

		// Do second rotation for root 
		return (root->right == NULL)? root: leftRotate(root); 
	} 
} 

// The search function for Splay tree. 
// Note that this function returns the 
// new root of Splay Tree. If key is 
// present in tree then, it is moved to root. 
node *search(node *root, int key) 
{ 
	return splay(root, key); 
} 

// A utility function to print 
// preorder traversal of the tree. 
// The function also prints height of every node 
void preOrder(node *root) 
{ 
	if (root != NULL) 
	{ 
		cout<<root->key<<" "; 
		preOrder(root->left); 
		preOrder(root->right); 
	} 
} 

/* Driver code*/
int main() 
{ 
	node *root = newNode(100); 
	root->left = newNode(50); 
	root->right = newNode(200); 
	root->left->left = newNode(40); 
	root->left->left->left = newNode(30); 
	root->left->left->left->left = newNode(20); 

	root = search(root, 20); 
	cout << "Preorder traversal of the modified Splay tree is \n"; 
	preOrder(root); 
	return 0; 
} 

// This code is contributed by rathbhupendra 
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

C

// The code is adopted from http://goo.gl/SDH9hH 
#include<stdio.h> 
#include<stdlib.h> 

// An AVL tree node 
struct node 
{ 
	int key; 
	struct node *left, *right; 
}; 

/* Helper function that allocates a new node with the given key and 
	NULL left and right pointers. */
struct node* newNode(int key) 
{ 
	struct node* node = (struct node*)malloc(sizeof(struct node)); 
	node->key = key; 
	node->left = node->right = NULL; 
	return (node); 
} 

// A utility function to right rotate subtree rooted with y 
// See the diagram given above. 
struct node *rightRotate(struct node *x) 
{ 
	struct node *y = x->left; 
	x->left = y->right; 
	y->right = x; 
	return y; 
} 

// A utility function to left rotate subtree rooted with x 
// See the diagram given above. 
struct node *leftRotate(struct node *x) 
{ 
	struct node *y = x->right; 
	x->right = y->left; 
	y->left = x; 
	return y; 
} 

// This function brings the key at root if key is present in tree. 
// If key is not present, then it brings the last accessed item at 
// root. This function modifies the tree and returns the new root 
struct node *splay(struct node *root, int key) 
{ 
	// Base cases: root is NULL or key is present at root 
	if (root == NULL || root->key == key) 
		return root; 

	// Key lies in left subtree 
	if (root->key > key) 
	{ 
		// Key is not in tree, we are done 
		if (root->left == NULL) return root; 

		// Zig-Zig (Left Left) 
		if (root->left->key > key) 
		{ 
			// First recursively bring the key as root of left-left 
			root->left->left = splay(root->left->left, key); 

			// Do first rotation for root, second rotation is done after else 
			root = rightRotate(root); 
		} 
		else if (root->left->key < key) // Zig-Zag (Left Right) 
		{ 
			// First recursively bring the key as root of left-right 
			root->left->right = splay(root->left->right, key); 

			// Do first rotation for root->left 
			if (root->left->right != NULL) 
				root->left = leftRotate(root->left); 
		} 

		// Do second rotation for root 
		return (root->left == NULL)? root: rightRotate(root); 
	} 
	else // Key lies in right subtree 
	{ 
		// Key is not in tree, we are done 
		if (root->right == NULL) return root; 

		// Zag-Zig (Right Left) 
		if (root->right->key > key) 
		{ 
			// Bring the key as root of right-left 
			root->right->left = splay(root->right->left, key); 

			// Do first rotation for root->right 
			if (root->right->left != NULL) 
				root->right = rightRotate(root->right); 
		} 
		else if (root->right->key < key)// Zag-Zag (Right Right) 
		{ 
			// Bring the key as root of right-right and do first rotation 
			root->right->right = splay(root->right->right, key); 
			root = leftRotate(root); 
		} 

		// Do second rotation for root 
		return (root->right == NULL)? root: leftRotate(root); 
	} 
} 

// The search function for Splay tree. Note that this function 
// returns the new root of Splay Tree. If key is present in tree 
// then, it is moved to root. 
struct node *search(struct node *root, int key) 
{ 
	return splay(root, key); 
} 

// A utility function to print preorder traversal of the tree. 
// The function also prints height of every node 
void preOrder(struct node *root) 
{ 
	if (root != NULL) 
	{ 
		printf("%d ", root->key); 
		preOrder(root->left); 
		preOrder(root->right); 
	} 
} 

/* Driver program to test above function*/
int main() 
{ 
	struct node *root = newNode(100); 
	root->left = newNode(50); 
	root->right = newNode(200); 
	root->left->left = newNode(40); 
	root->left->left->left = newNode(30); 
	root->left->left->left->left = newNode(20); 

	root = search(root, 20); 
	printf("Preorder traversal of the modified Splay tree is \n"); 
	preOrder(root); 
	return 0; 
} 

      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

Java

// Java implementation for above approach 
class GFG 
{ 

// An AVL tree node 
static class node 
{ 

	int key; 
	node left, right; 
}; 

/* Helper function that allocates 
a new node with the given key and 
	null left and right pointers. */
static node newNode(int key) 
{ 
	node Node = new node(); 
	Node.key = key; 
	Node.left = Node.right = null; 
	return (Node); 
} 

// A utility function to right 
// rotate subtree rooted with y 
// See the diagram given above. 
static node rightRotate(node x) 
{ 
	node y = x.left; 
	x.left = y.right; 
	y.right = x; 
	return y; 
} 

// A utility function to left 
// rotate subtree rooted with x 
// See the diagram given above. 
static node leftRotate(node x) 
{ 
	node y = x.right; 
	x.right = y.left; 
	y.left = x; 
	return y; 
} 

// This function brings the key at 
// root if key is present in tree. 
// If key is not present, then it 
// brings the last accessed item at 
// root. This function modifies the 
// tree and returns the new root 
static node splay(node root, int key) 
{ 
	// Base cases: root is null or 
	// key is present at root 
	if (root == null || root.key == key) 
		return root; 

	// Key lies in left subtree 
	if (root.key > key) 
	{ 
		// Key is not in tree, we are done 
		if (root.left == null) return root; 

		// Zig-Zig (Left Left) 
		if (root.left.key > key) 
		{ 
			// First recursively bring the 
			// key as root of left-left 
			root.left.left = splay(root.left.left, key); 

			// Do first rotation for root, 
			// second rotation is done after else 
			root = rightRotate(root); 
		} 
		else if (root.left.key < key) // Zig-Zag (Left Right) 
		{ 
			// First recursively bring 
			// the key as root of left-right 
			root.left.right = splay(root.left.right, key); 

			// Do first rotation for root.left 
			if (root.left.right != null) 
				root.left = leftRotate(root.left); 
		} 

		// Do second rotation for root 
		return (root.left == null) ? 
							root : rightRotate(root); 
	} 
	else // Key lies in right subtree 
	{ 
		// Key is not in tree, we are done 
		if (root.right == null) return root; 

		// Zag-Zig (Right Left) 
		if (root.right.key > key) 
		{ 
			// Bring the key as root of right-left 
			root.right.left = splay(root.right.left, key); 

			// Do first rotation for root.right 
			if (root.right.left != null) 
				root.right = rightRotate(root.right); 
		} 
		else if (root.right.key < key)// Zag-Zag (Right Right) 
		{ 
			// Bring the key as root of 
			// right-right and do first rotation 
			root.right.right = splay(root.right.right, key); 
			root = leftRotate(root); 
		} 

		// Do second rotation for root 
		return (root.right == null) ? 
							root : leftRotate(root); 
	} 
} 

// The search function for Splay tree. 
// Note that this function returns the 
// new root of Splay Tree. If key is 
// present in tree then, it is moved to root. 
static node search(node root, int key) 
{ 
	return splay(root, key); 
} 

// A utility function to print 
// preorder traversal of the tree. 
// The function also prints height of every node 
static void preOrder(node root) 
{ 
	if (root != null) 
	{ 
		System.out.print(root.key + " "); 
		preOrder(root.left); 
		preOrder(root.right); 
	} 
} 

// Driver code 
public static void main(String[] args) 
{ 
	node root = newNode(100); 
	root.left = newNode(50); 
	root.right = newNode(200); 
	root.left.left = newNode(40); 
	root.left.left.left = newNode(30); 
	root.left.left.left.left = newNode(20); 

	root = search(root, 20); 
	System.out.print("Preorder traversal of the" + 
					" modified Splay tree is \n"); 
	preOrder(root); 
} 
} 

// This code is contributed by 29AjayKumar 

      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

C#

// C# implementation for above approach 
using System; 

class GFG 
{ 

// An AVL tree node 
public class node 
{ 

	public int key; 
	public node left, right; 
}; 

/* Helper function that allocates 
a new node with the given key and 
null left and right pointers. */
static node newNode(int key) 
{ 
	node Node = new node(); 
	Node.key = key; 
	Node.left = Node.right = null; 
	return (Node); 
} 

// A utility function to right 
// rotate subtree rooted with y 
// See the diagram given above. 
static node rightRotate(node x) 
{ 
	node y = x.left; 
	x.left = y.right; 
	y.right = x; 
	return y; 
} 

// A utility function to left 
// rotate subtree rooted with x 
// See the diagram given above. 
static node leftRotate(node x) 
{ 
	node y = x.right; 
	x.right = y.left; 
	y.left = x; 
	return y; 
} 

// This function brings the key at 
// root if key is present in tree. 
// If key is not present, then it 
// brings the last accessed item at 
// root. This function modifies the 
// tree and returns the new root 
static node splay(node root, int key) 
{ 
	// Base cases: root is null or 
	// key is present at root 
	if (root == null || root.key == key) 
		return root; 

	// Key lies in left subtree 
	if (root.key > key) 
	{ 
		// Key is not in tree, we are done 
		if (root.left == null) return root; 

		// Zig-Zig (Left Left) 
		if (root.left.key > key) 
		{ 
			// First recursively bring the 
			// key as root of left-left 
			root.left.left = splay(root.left.left, key); 

			// Do first rotation for root, 
			// second rotation is done after else 
			root = rightRotate(root); 
		} 
		else if (root.left.key < key) // Zig-Zag (Left Right) 
		{ 
			// First recursively bring 
			// the key as root of left-right 
			root.left.right = splay(root.left.right, key); 

			// Do first rotation for root.left 
			if (root.left.right != null) 
				root.left = leftRotate(root.left); 
		} 

		// Do second rotation for root 
		return (root.left == null) ? 
							root : rightRotate(root); 
	} 
	else // Key lies in right subtree 
	{ 
		// Key is not in tree, we are done 
		if (root.right == null) return root; 

		// Zag-Zig (Right Left) 
		if (root.right.key > key) 
		{ 
			// Bring the key as root of right-left 
			root.right.left = splay(root.right.left, key); 

			// Do first rotation for root.right 
			if (root.right.left != null) 
				root.right = rightRotate(root.right); 
		} 
		else if (root.right.key < key)// Zag-Zag (Right Right) 
		{ 
			// Bring the key as root of 
			// right-right and do first rotation 
			root.right.right = splay(root.right.right, key); 
			root = leftRotate(root); 
		} 

		// Do second rotation for root 
		return (root.right == null) ? 
							root : leftRotate(root); 
	} 
} 

// The search function for Splay tree. 
// Note that this function returns the 
// new root of Splay Tree. If key is 
// present in tree then, it is moved to root. 
static node search(node root, int key) 
{ 
	return splay(root, key); 
} 

// A utility function to print 
// preorder traversal of the tree. 
// The function also prints height of every node 
static void preOrder(node root) 
{ 
	if (root != null) 
	{ 
		Console.Write(root.key + " "); 
		preOrder(root.left); 
		preOrder(root.right); 
	} 
} 

// Driver code 
public static void Main(String[] args) 
{ 
	node root = newNode(100); 
	root.left = newNode(50); 
	root.right = newNode(200); 
	root.left.left = newNode(40); 
	root.left.left.left = newNode(30); 
	root.left.left.left.left = newNode(20); 

	root = search(root, 20); 
	Console.Write("Preorder traversal of the" + 
				" modified Splay tree is \n"); 
	preOrder(root); 
} 
} 

// This code is contributed by 29AjayKumar 
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

:

Preorder traversal of the modified Splay tree is 20 50 30 40 100 200

1) Splay- . . .

2) splay- O(log n). , Splay- O(log n) ( , )

3) Splay- - -, splay- .

4) -, splay- , .

Splay-

Splay- , 30 , .

Splay- Windows NT ( , ), gcc GNU C++, sed, Fore Systems, Unix malloc, Linux (: http://www.cs.berkeley.edu/~jrs/61b/lec/36)

Splay Tree | Set 2 (Insert).

:

http://www.cs.berkeley.edu/~jrs/61b/lec/36

http://www.cs.cornell.edu/courses/cs3110/2009fa/recitations/rec-splay.html

http://courses.cs.washington.edu/courses/cse326/01au/lectures/SplayTrees.ppt

---

" ".



" ."

OTUS . .   OTUS.

, " " -   .