Bonne année 2021 à Habr et Habrazhateli et présentez-nous à tous un arbre de Noël fonctionnel sans prétention et agréable (fYolka). Dans cet article, je vais vous dire comment faire un sapin de Noël sur le moniteur en 10 minutes. Je vais consacrer mon deuxième article à comment «mouler» un bonhomme de neige, mettre des cadeaux sous l'arbre et saupoudrer le tout de neige sur le dessus.
Idée basique
La figure entière est un ensemble de fonctions mathématiques à partir de deux arguments, x et y. Tous sont basés sur SDF d'une manière ou d'une autre . Desmos.com a été utilisé pour dessiner les graphiques .
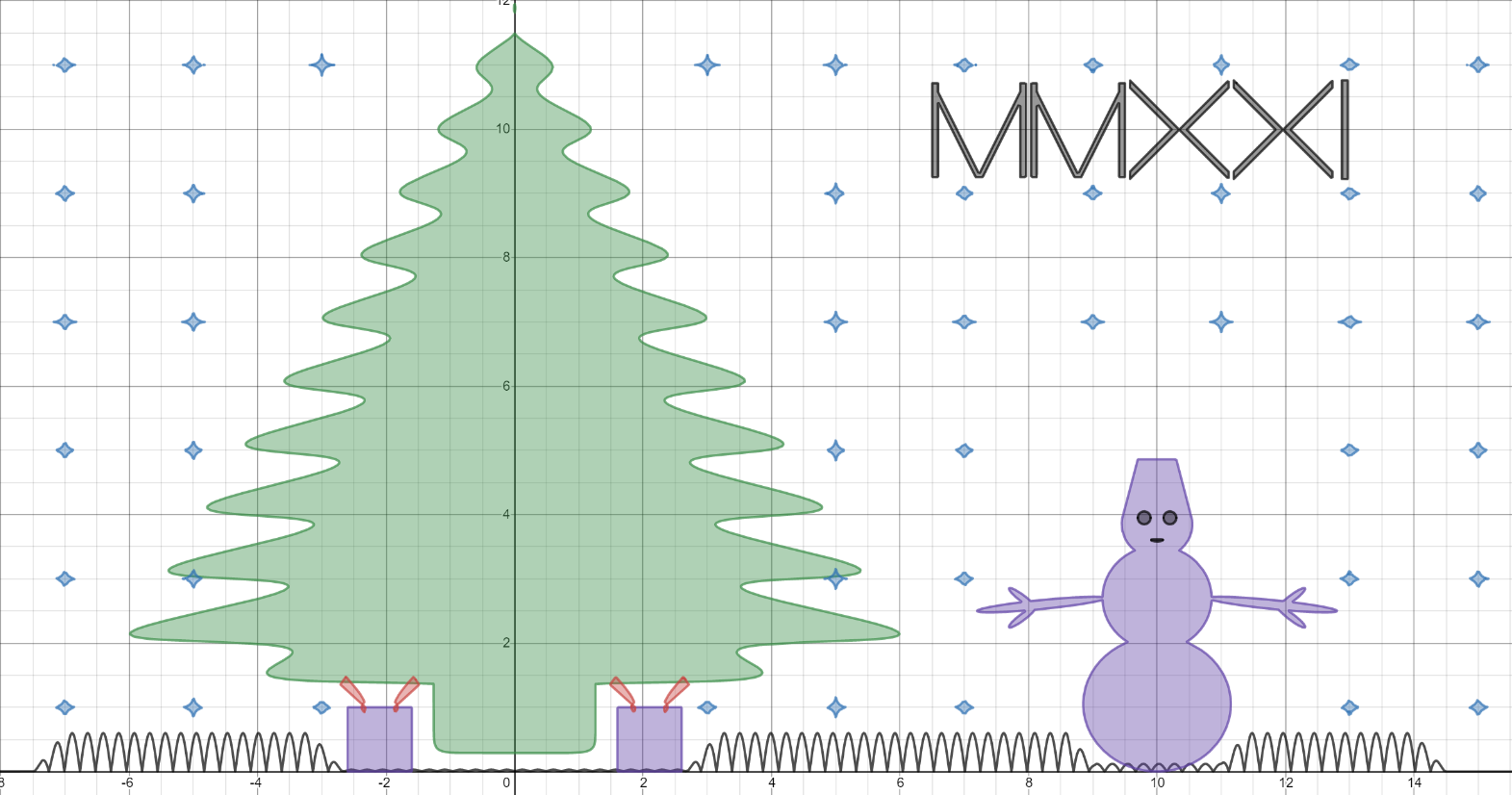
Les fonctions de base
Limite zéro

Ellipse

Sapin de Noël
Décrivons la base de l'arbre

Ajouter des branches
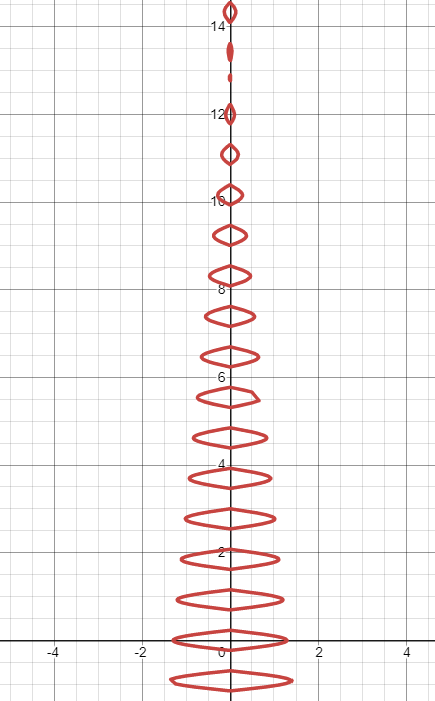
Amenez les pointes des branches au sol

Limiter l'épicéa d'en haut
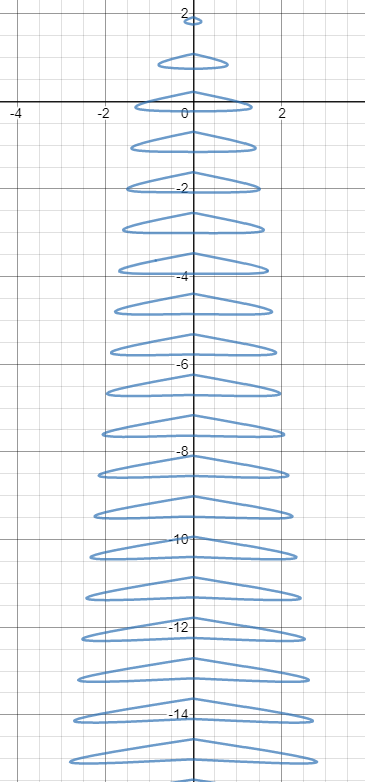
Épicéa déplacé vers le bas, cela sera corrigé plus tard
Course parallèle: limite par le bas
Limiteur
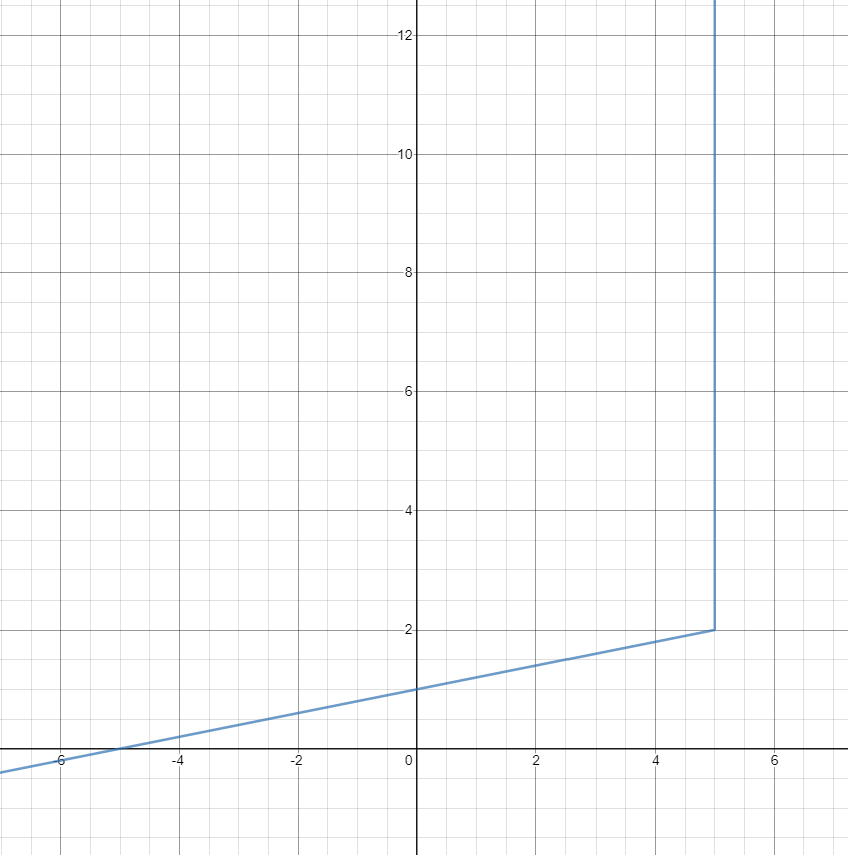
Le résultat de cette étape
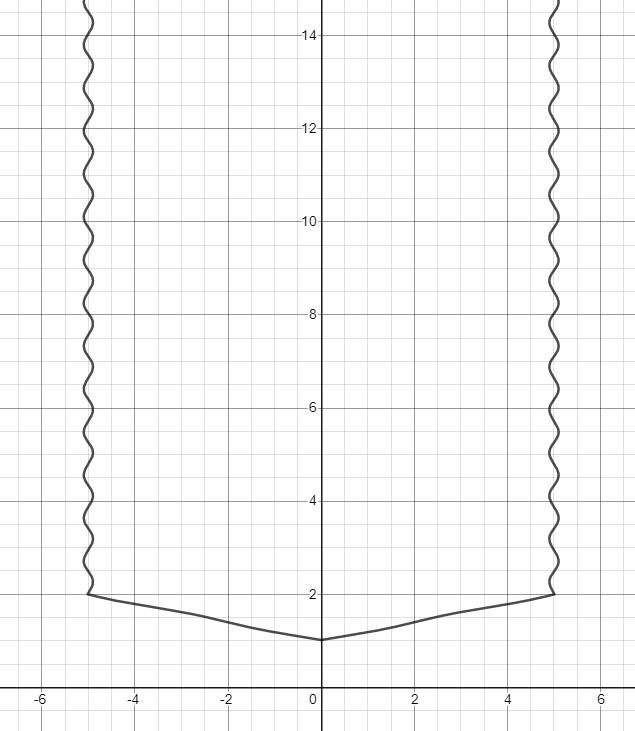
Nous combinons

La touche finale
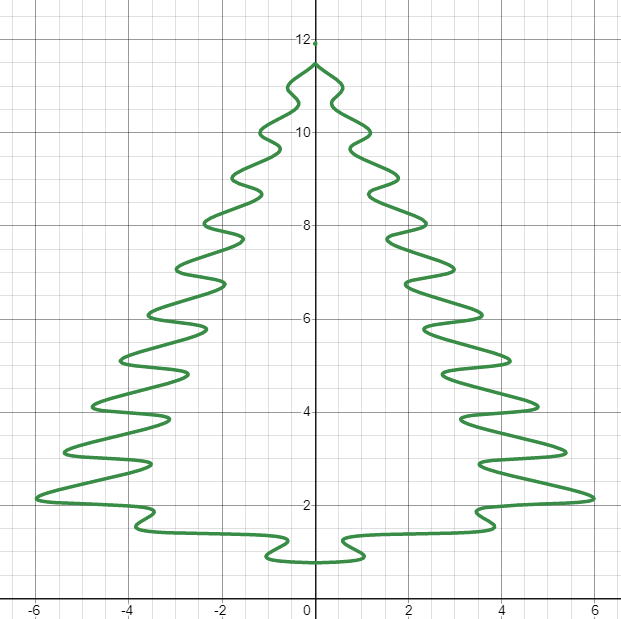
Traitons du coffre
Ellipse avec des coins plus nets
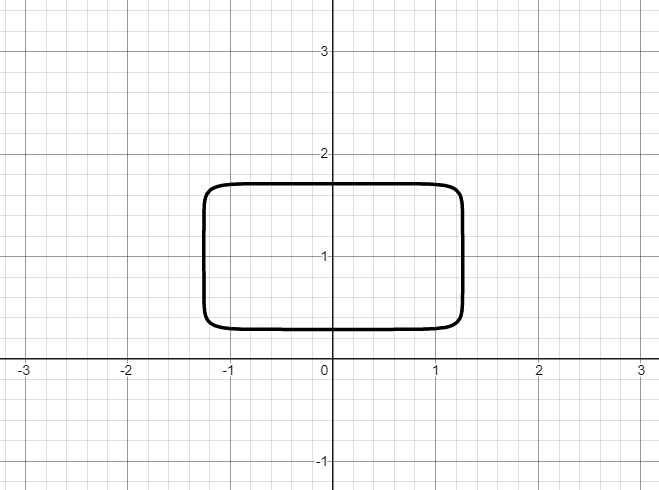
Combiner des objets
L'union, l'intersection et la coupe sont basées sur l'opération min (a, b) la plus simple. En fonction des signes devant a et b, différentes opérations booléennes sont obtenues.
Feuillage - a (xy), tronc - b (xy)

Le final

Toutes les formules à intégrer dans desmos.com
a = 2-0,2 \ cos \ gauche (6,8y + 0,7 \ gauche | x \ droite | \ droite) \ gauche (y-13 \ droite) -2 \ gauche | x \ droite | -0,51 \ gauche (y + \ gauche | y \ droite | \ droite) +5 \ gauche (y- \ gauche | y-2 \ droite | \ droite)
b \ = \ 0,1x ^ {10} +30 \ gauche (y-1 \ droite) ^ {10} -1
\ min \ gauche (-a, \ b \ droite) \ le0
À suivre...