Suite de l'article d' hier sur fYolka, ci-dessous.
Les fonctions de base
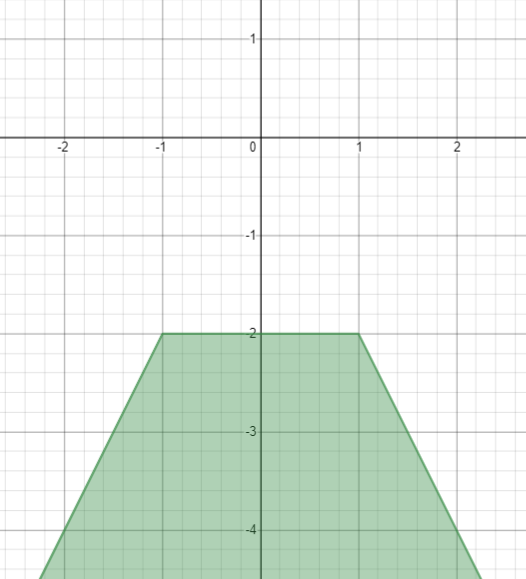
Trapèze
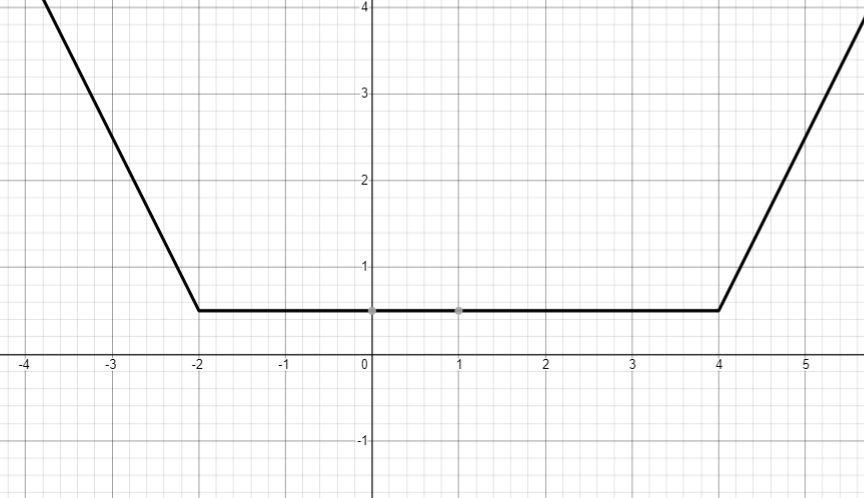
Ici, le module du nombre est appliqué deux fois, en changeant les constantes sous le module et la soustraite, nous pouvons ajuster la longueur du segment avec une valeur constante y et la valeur de y lui-même sur ce segment. Cette fonctionnalité sera utile plus tard pour les dérives et les seaux.
Ellipse alternative
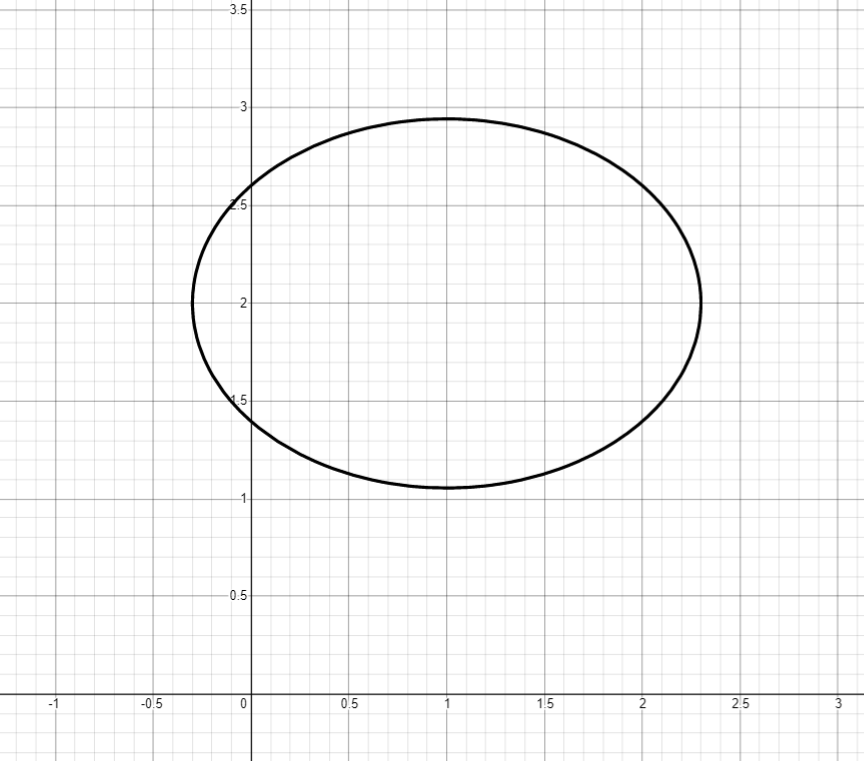
Notation alternative d'ellipse. Les constantes à l'intérieur des crochets sont responsables des coordonnées du centre de l'ellipse, les constantes devant les crochets sont pour le taux de compression le long des axes, le nombre derrière la racine est le rayon.
Ellipse par deux points

, - , (A B ) . .
, .
- :
-
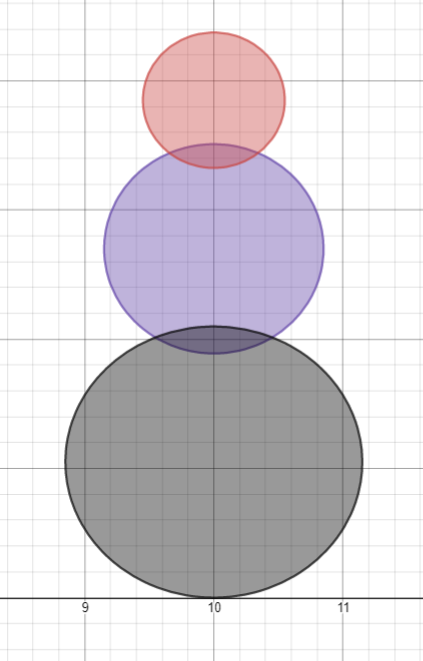
- min .

!
-
- ,

, - 2 , - .
-
, .
:

,

-

-


s4 , >0, <0, .
-
- x = 10, , , .
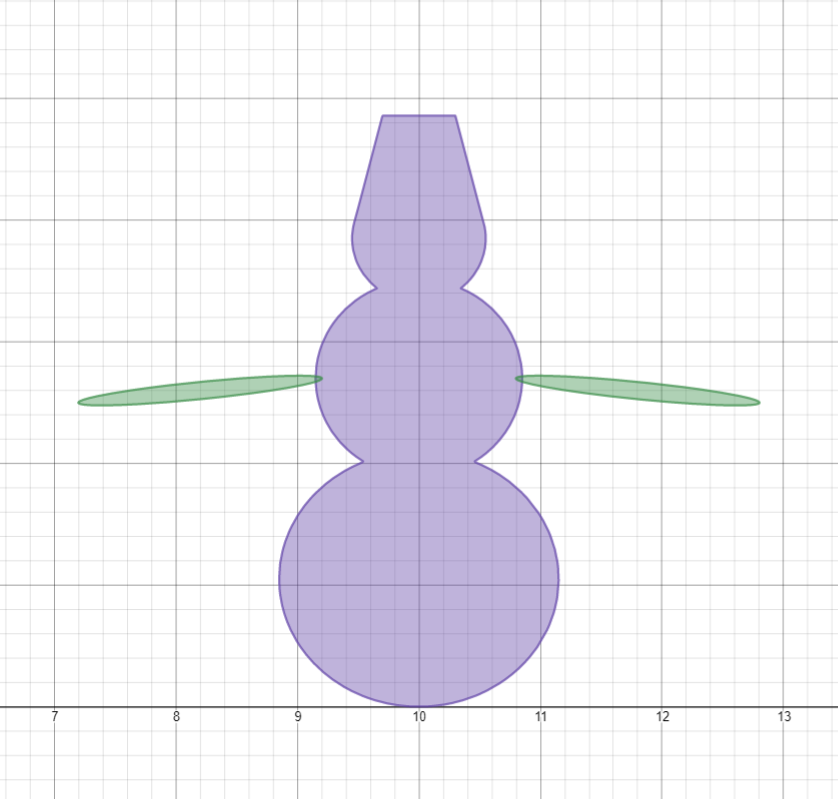
, = 10, = 2.55

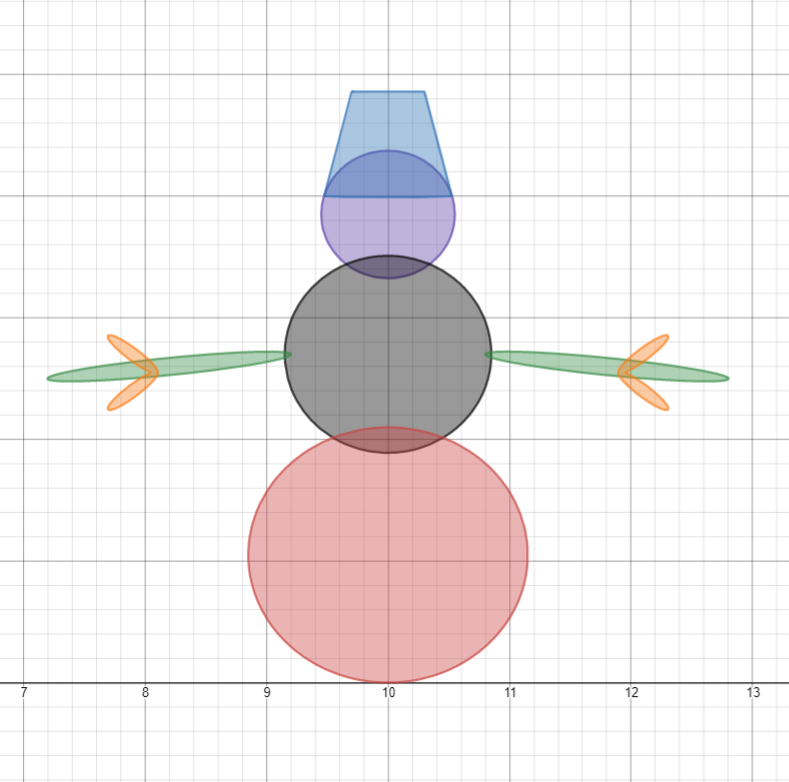

- 2

-

desmos
s_{1}=\sqrt{\left(x-10\right)^{2}+1.1\left(y-2.7\right)^{2}}-0.85
s_{2}=\sqrt{\left(x-10\right)^{2}+1.2\left(y-1.05\right)^{2}}-1.15
s_{3}=\sqrt{\left(x-10\right)^{2}+1.1\left(y-3.85\right)^{2}}-0.55
s_{4}=2-1.9\left|x-9.7\right|-1.9\left|x-10.3\right|-\left(\frac{\left(\left|y-4\right|+y-4\right)}{2}+\frac{100\left(\left|y-4\right|-y+4\right)}{2}\right)
h_{1}=\sqrt{\left(\left|x-10\right|\ -\ 0.8\right)^{2}+\left(y-2.7\right)^{2}}+\sqrt{\left(\left|x-10\right|\ -\ 2.8\right)^{2}+\left(y-2.5\right)^{2}}-2.015
h_{2}=\sqrt{\left(\left|x-10\right|\ -\ 1.9\right)^{2}+\left(y-2.55\right)^{2}}+\sqrt{\left(\left|x-10\right|\ -\ 2.3\right)^{2}+\left(\left|y-2.55\right|-0.3\right)^{2}}-0.51
\min\left(s_{1},\ s_{2},s_{3},-s_{4},h_{1},h_{2}\right)\le0
100\left(\left|x-10\right|-0.2\right)^{2}+100\left(y-3.95\right)^{2}\le1
\left(300\left(\left|x-10\right|-0.03-0.-\left(y-3.6\right)\right)^{2}+3000\left(y-3.6\right)^{2}\right)\le1
- . .

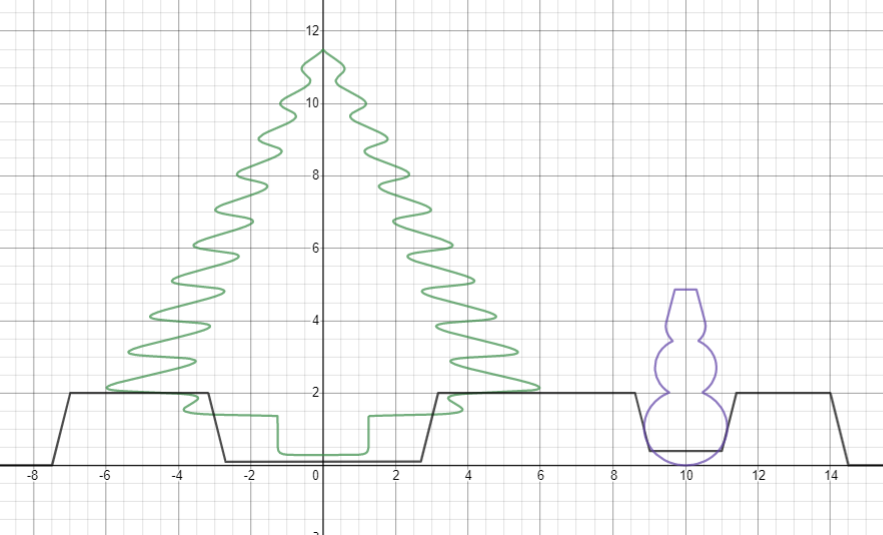
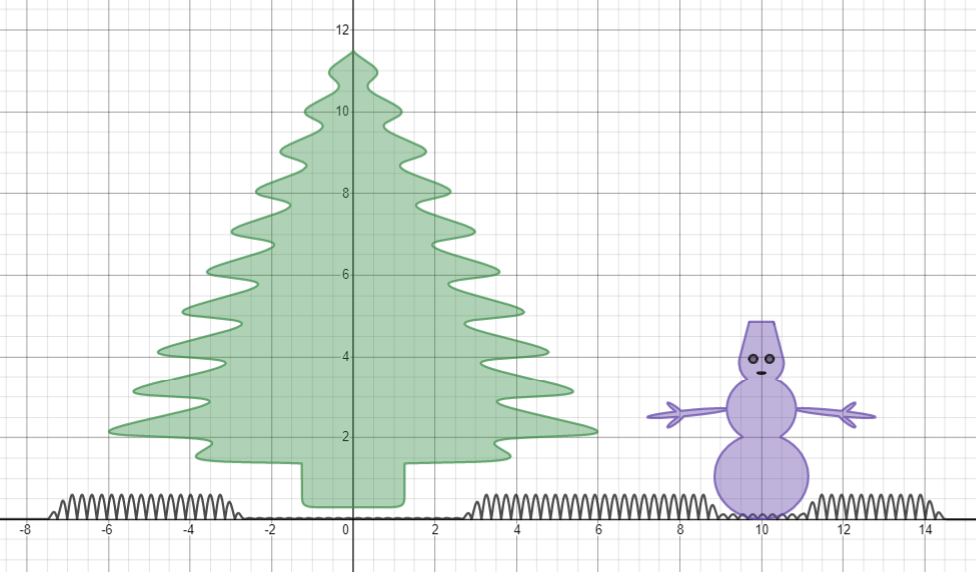
d_{1}=-\left|x+7\right|-\left|x-14\right|+22
d_{2}=\left|x+2.7\right|+\left|x-2.7\right|-6.35
d_{3}=\left|x-9\right|+\left|x-11\right|-2.8
d=d_{1}+\left|d_{1}\right|+d_{2}-\left|d_{2}\right|+d_{3}-\left|d_{3}\right|
0.3d\left|\sin\left(13x\right)\right|
. - " ", , , x .

mod,


, .
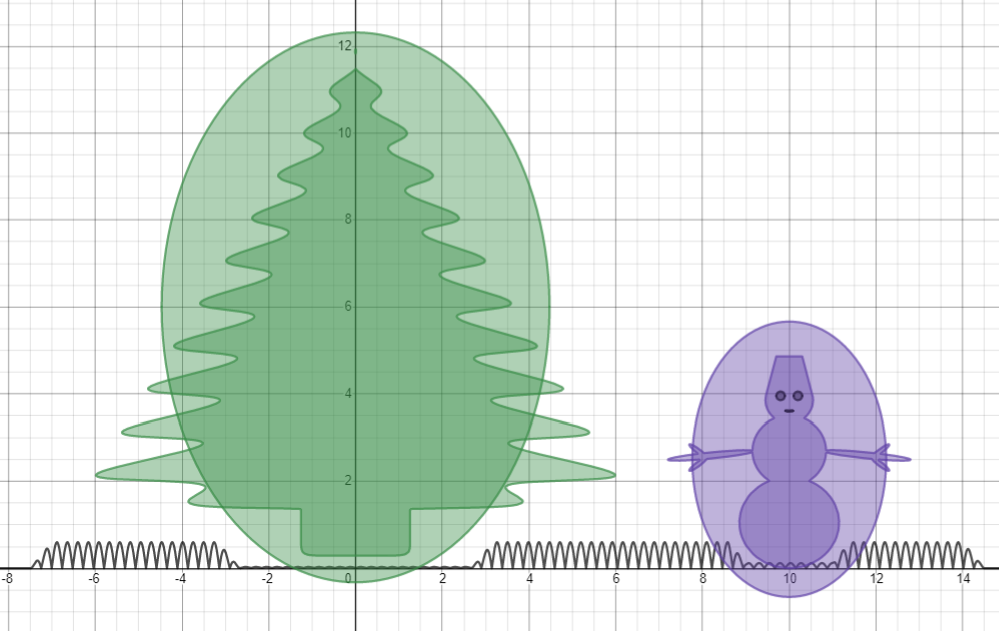

f_{1}=\sqrt{\left|\operatorname{mod}\left(x,2\right)-1\right|}+\sqrt{\left|\operatorname{mod}\left(y,2\right)-1\right|}-0.45
f_{2}=2xx+\left(y-6\right)^{2}-40
f_{3}=2\left(x-10\right)^{2}+\left(y-2.5\right)^{2}-10
\min\left(-f_{1},f_{2},f_{3}\right)\ge0
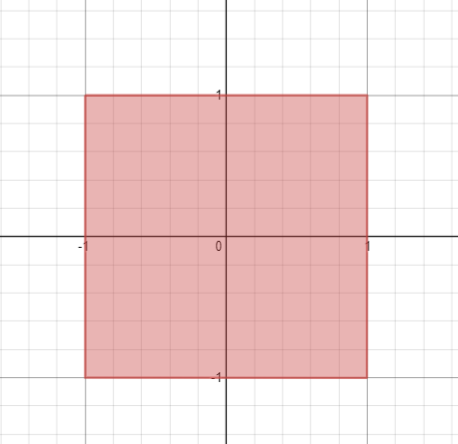
- . , |x| .
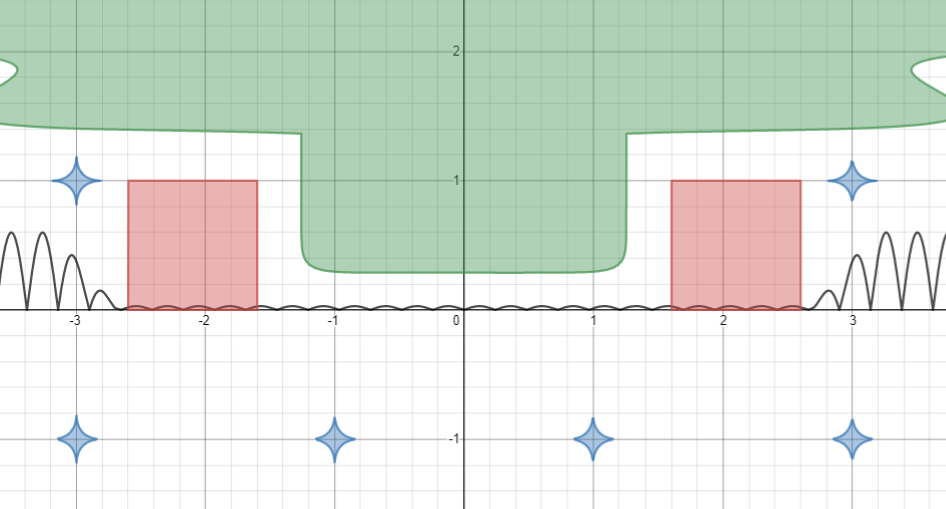
\max\left(\left|\left|x\right|-2.1\right|,\left|y-0.5\right|\right)\le0.5

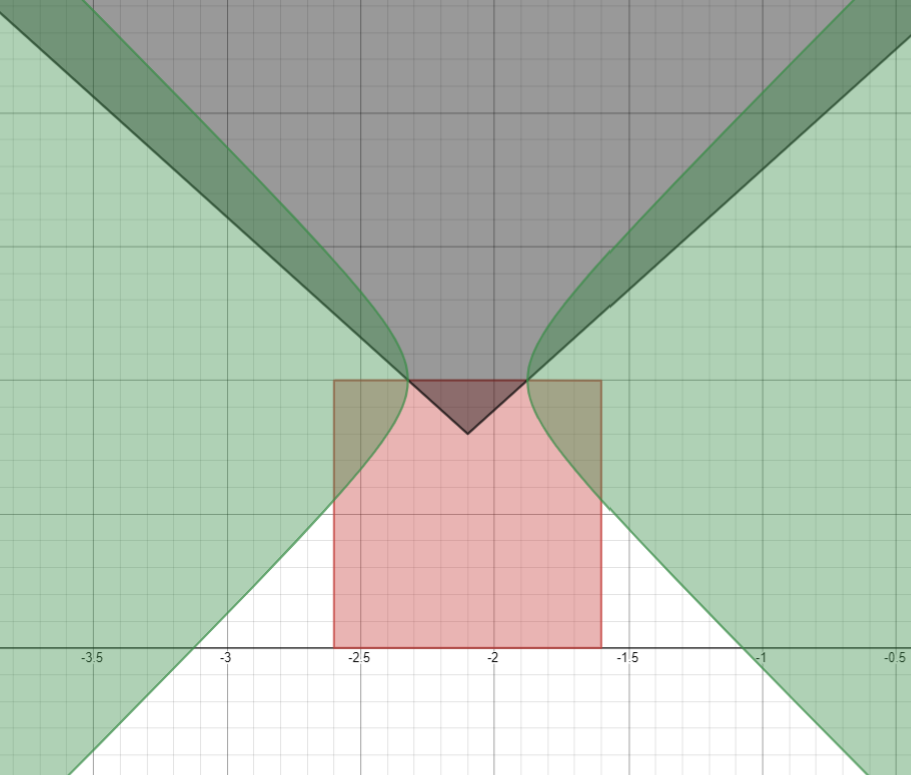

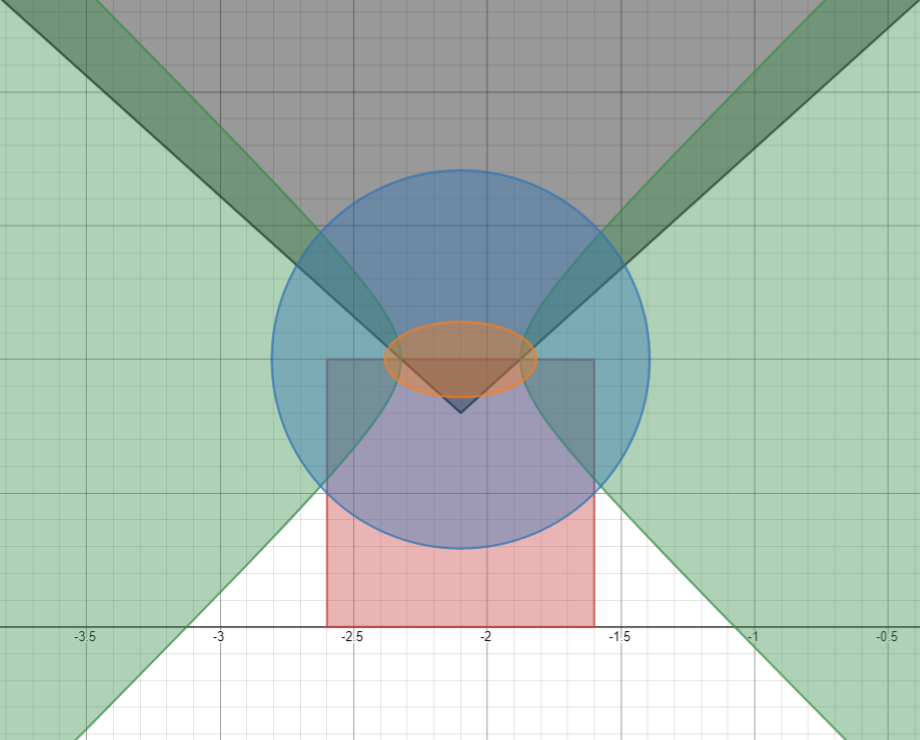
:
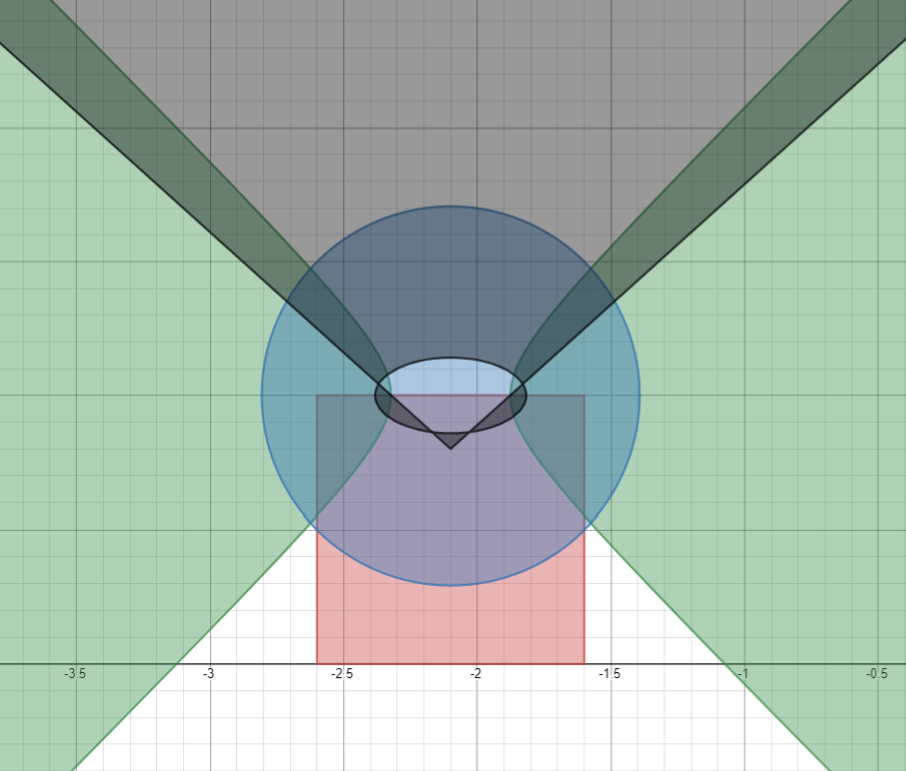
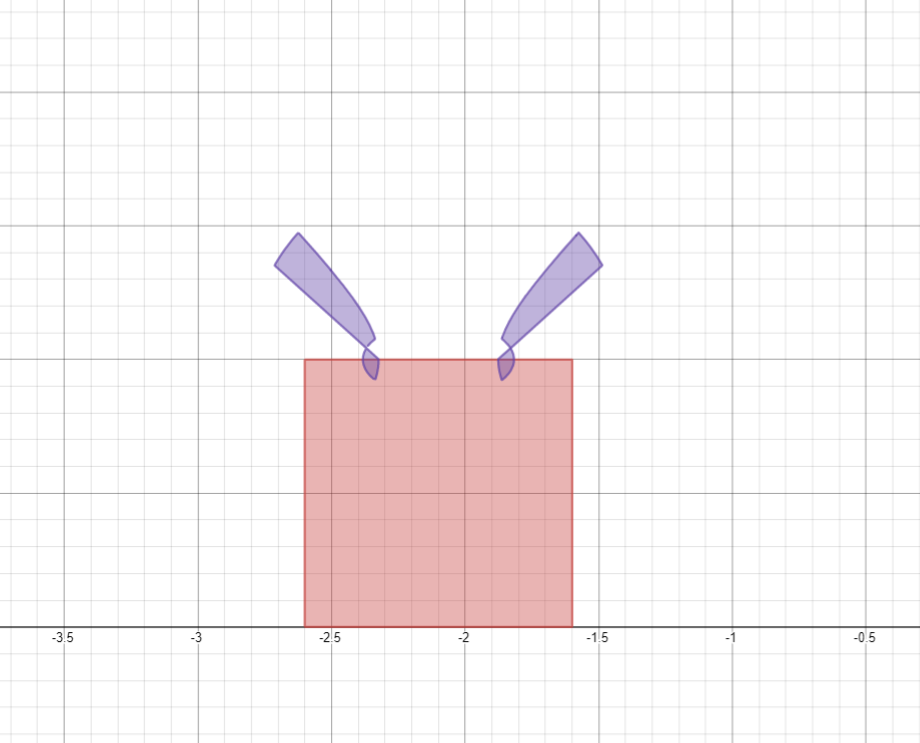
j_{1}=\left|0.9\left|\left|x\right|-2.1\right|\right|-\left(y-1\right)-0.2
j_{2}=\left|\left|x\right|-2.1\right|^{2}-\left(y-1\right)^{2}-0.05
j_{3}=0.2\left|\left|x\right|-2.1\right|^{2}+0.2\left(y-1\right)^{2}-0.1
j_{4}=\left(0.5\left|\left|x\right|-2.1\right|\right)^{2}+\left(y-1\right)^{2}-0.02
\max\left(j_{1}j_{4},\ -j_{2},\ j_{3}\right)\le0
, , .
2021 MMXXI,
""
t2,

"",

V-
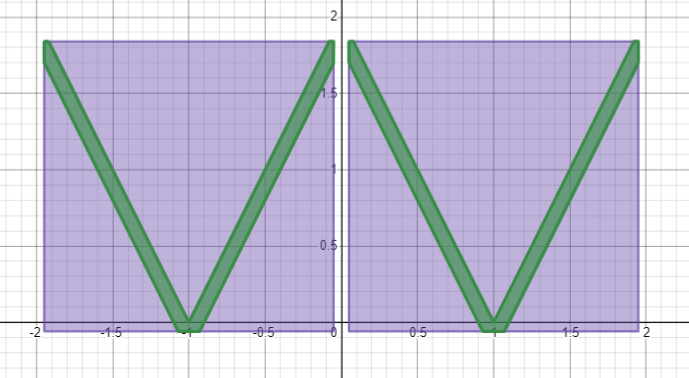
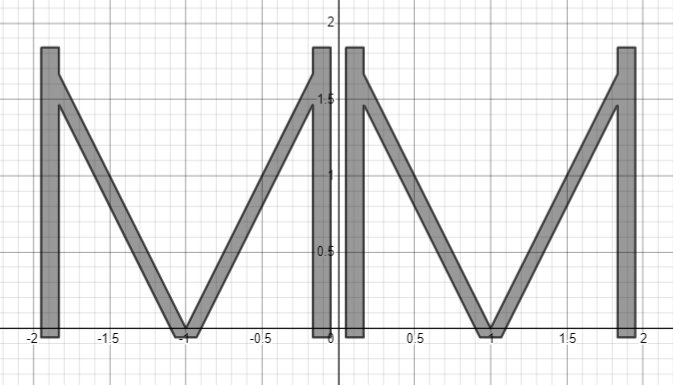
""
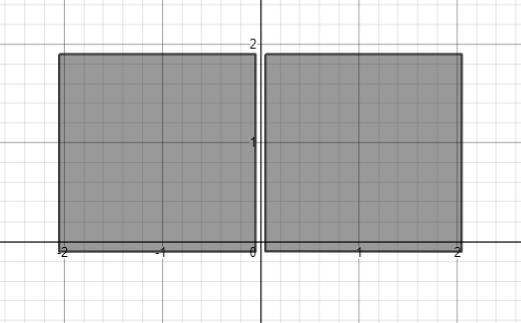

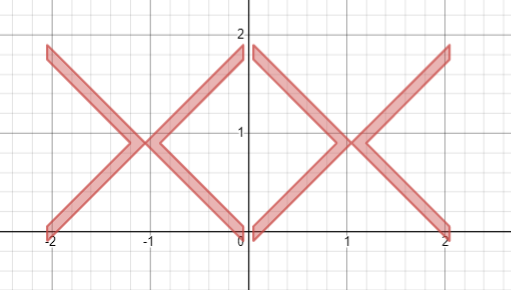
4.1 ,
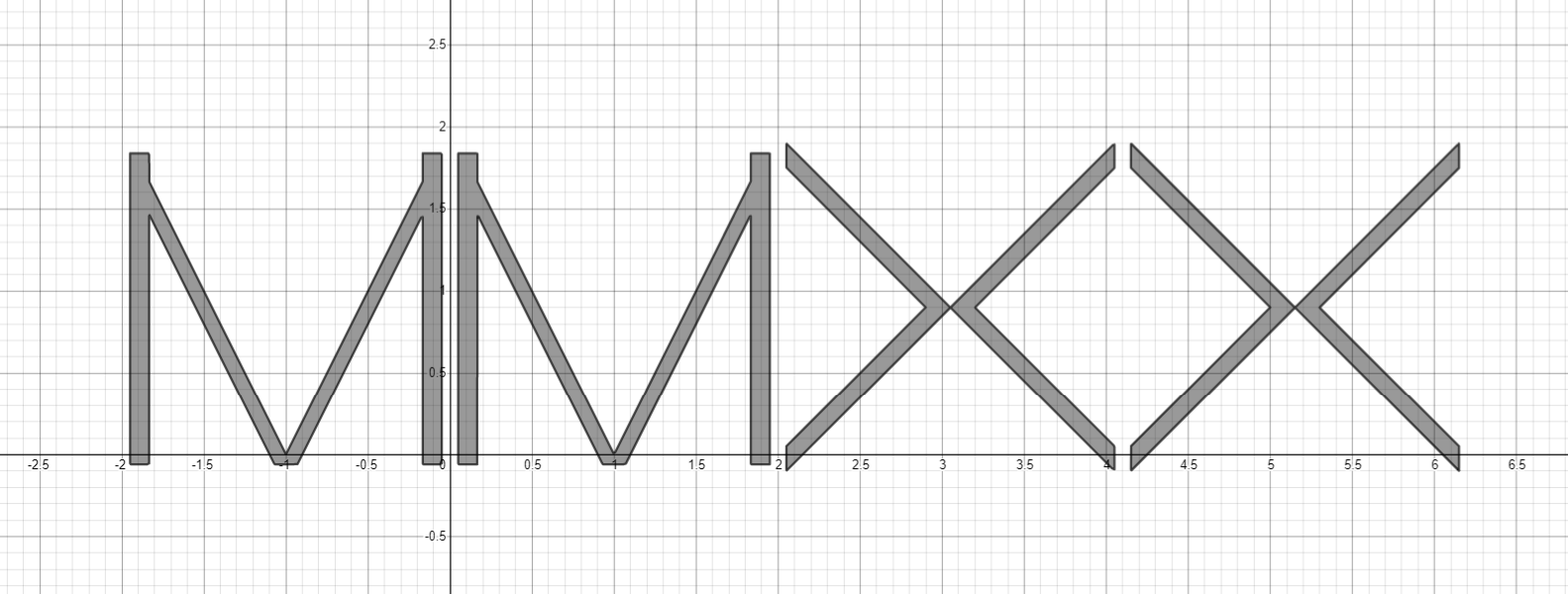
"I"
, "I"
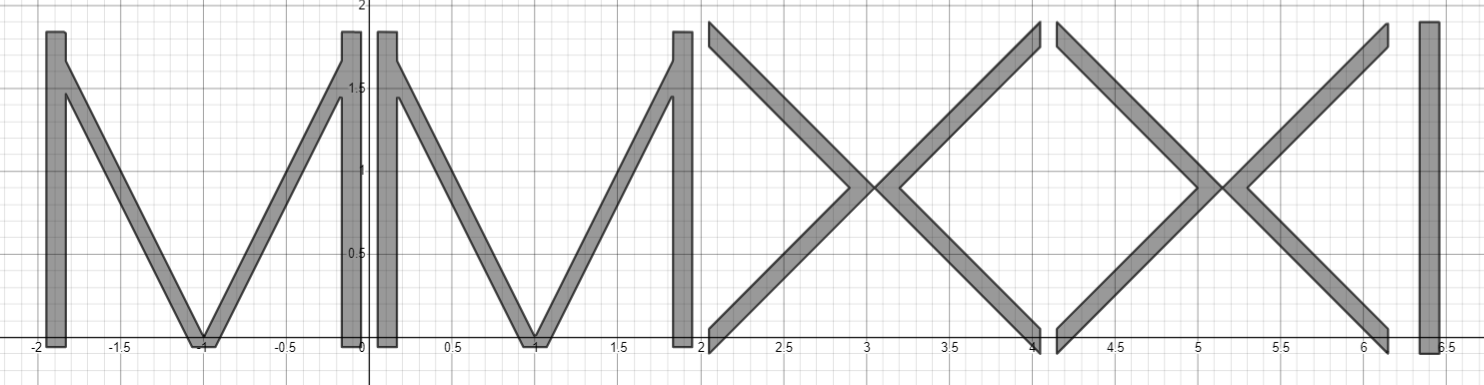
t_{2}=\max\left(\left|\left|x_{1}\right|-1\right|,\left|y_{1}-0.89\right|\right)-0.95
\max\left(\min\left(-t_{2},\max\left(\left|1.2\left|x_{1}\right|-1.2\right|,\left|y_{1}-0.9\right|\right)-1\right),\min\left(\left|2\left|x_{1}\right|-2\right|-y_{1},-\left|2\left|x_{1}\right|-2\right|+y_{1}+0.2,-t_{2}\right)\right)\ge0
\max\left(-\min\left(\left|\left|x_{1}-4.1\right|-1.05\right|-\left|y_{1}-0.9\right|,\ -\left|\left|x_{1}-4.1\right|-1.05\right|+\left|y_{1}-0.9\right|+0.15\right),\max\left(\left|\left|x_{1}-4.1\right|-1.05\right|,\left|y_{1}-0.9\right|\right)-1\right)\le0

, - , , , sin(x), x∈(-5, 5). .
:
Par conséquent, l'utilisation des fonctions min et max dans les formules de figure est légale dans cette tâche.