👩🏼‍🤝‍👨🏻 💃🏿 🤽🏻 Représentation visuelle de la factorisation d'un nombre à l'aide de fonctions trigonométriques 🌜 ➰ 👩🏽‍🍳

Prenons une hyperbole de la forme:

Ici n est un nombre impair dont il faut trouver les diviseurs. Multipliez f (x) par cos [π⋅f (x)] (note - les crochets () et [] sont équivalents et n'ajoutent pas de significations supplémentaires). Et prenez le module de la fonction résultante g (x):

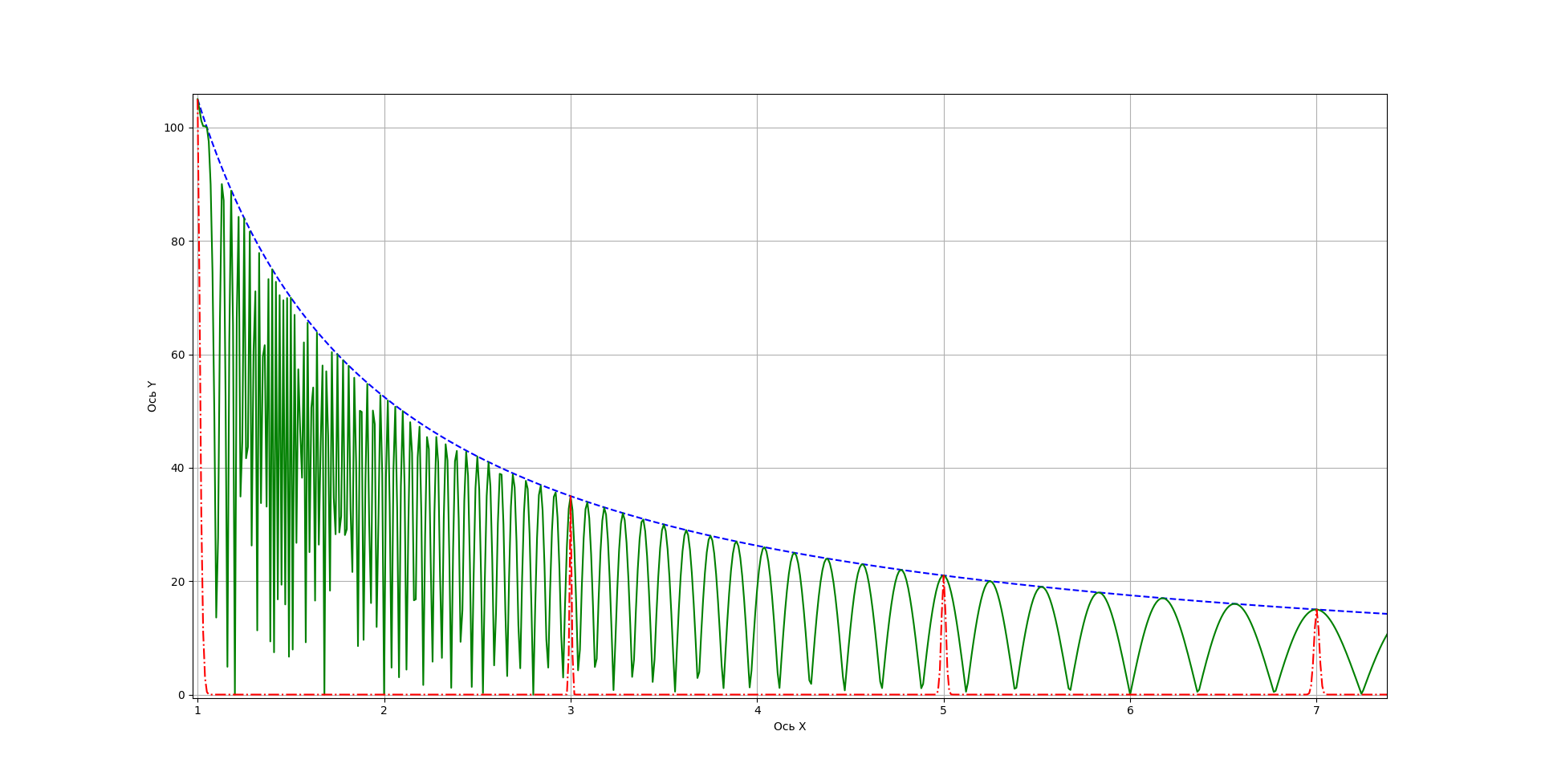
Les graphes f (x) et | g (x) | sont représentés sur la Fig. 1. n est pris égal à 15. Et c'est l'un des principaux inconvénients de la méthode, pour de grandes valeurs de n, l'argument du cosinus change avec une fréquence très élevée.

Figure 1 - Graphique des fonctions f (x) = 35 / x et | g (x) | = | f (x) ⋅cos [π⋅f (x)] | — 1 - f(x)=35/x |g(x)|=|f(x)⋅cos[π⋅f(x)]|

, , 2 .

Figure 2 - Graphique de la fonction f (x) ⋅cos [π⋅f (x)] ^ 10 — 2 - f(x)⋅cos[π⋅f(x)]^10

"" (. . 3) (.. g(x)) [sin(π⋅x/2)⋅sin(3π⋅x/2)⋅sin(5π⋅x/2)⋅sin(7π⋅x/2)]^20.

n. 1, 3, 5, 15.

Figure 3 - Filtrage de f (x) ⋅cos [π⋅f (x)] ^ 10 en utilisant sin (π⋅n⋅x / 2) — 3 - f(x)⋅cos[π⋅f(x)]^10 sin(π⋅n⋅x/2)

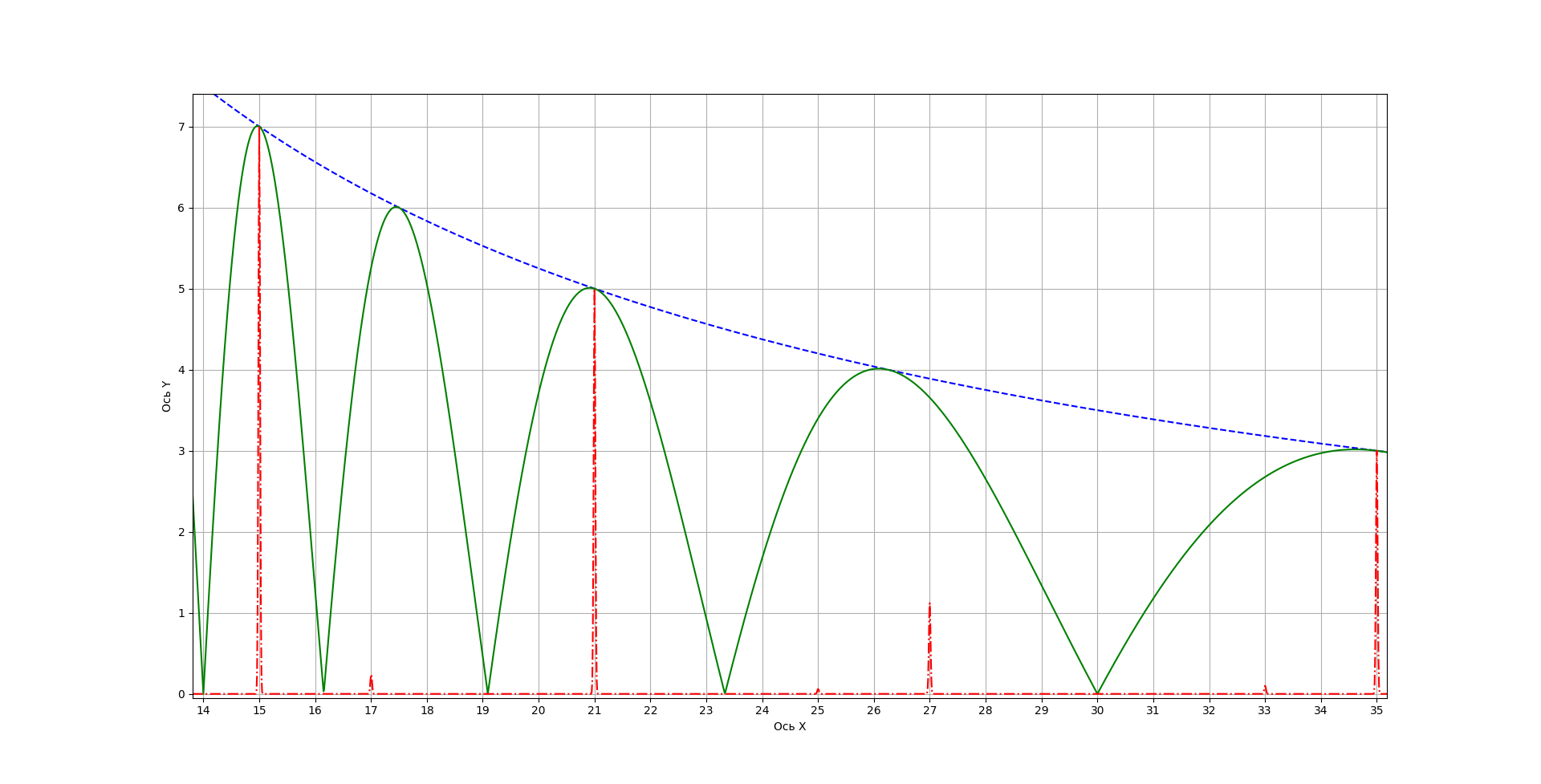
n=105, 4, 5 1, 3, 5, 7, 15, 21, 35. 105 .

Figure 4 - Hyperbole f (x) = 105 / x et diviseurs possibles — 4 - f(x)=105/x

Figure 5 - Hyperbole f (x) = 105 / x et diviseurs possibles (suite) — 5 - f(x)=105/x ()

"" , .

.. , p-V-T , . . 6 10.

Figure 6 - Multiplicateurs des nombres 21, 77, 187, 323, 437 en 3D. — 6 - 21, 77, 187, 323, 437 3D.

(-cos[π⋅f(x)]) :

1 n N_n=(n-1)/2
N x N_x=n⋅(x-1)/2⋅x
La coordonnée x de la Nième période est calculée par la formule x _N = n / (n-2⋅N)
Le rapport de la valeur de coordonnée x _{N + 1} à x _N : x _{N + 1} / x _N = 1 + 2 / (n-2⋅N)
Si vous imaginez un nombre assez grand n comme le produit de P (1 + 2 / (n-2⋅N)) de 1 à N _n , le premier ≈63,2% des termes du produit donnera le nombre e.

Représentation visuelle de la factorisation d'un nombre à l'aide de fonctions trigonométriques

More articles: