La malédiction de Tsiolkovsky et la grâce d'Obert

Bonjour, chers lecteurs de Habr.



Nous continuons à étudier la mécanique orbitale sur un doigt et deux énergies. Dans cet article, vous découvrirez la formule Tsiolkovsky, l'effet Obert, la différence entre l'énergie et l'élan, le fonctionnement des fusées et tout cela en utilisant les exemples les plus simples avec une forte géométrie à 90 degrés.

L'effet Aubert

Commençons par l'effet Aubert, bien qu'il s'agisse d'un effet extrêmement complexe, mais après l'avoir traité, nous comprendrons toute la physique orbitale. Tout d'abord, posons-nous une question - Quelle est la force, frère? - En chevaux!



Quelle est la puissance d'un moteur de fusée?



La réponse est étrange - de différentes manières, le même kilogramme de carburant dans le même moteur donne une quantité d'énergie différente. La raison en est la vitesse différente à laquelle ce carburant est utilisé, plus la vitesse de la fusée elle-même est élevée, plus le moteur donne d'énergie, et le même moteur accélérant latéralement (par rapport à la vitesse actuelle) donnera moins d'énergie que lors d'une accélération vers l'avant.



Regardons tout de suite 2 bons exemples illustratifs. Un de YouTube du garage scientifique Igor Beletsky qui a démontré l'effet Obert avec une seringue, un élastique et autre chose, et le deuxième exemple est de Wikipedia.

Expérience artisanale.

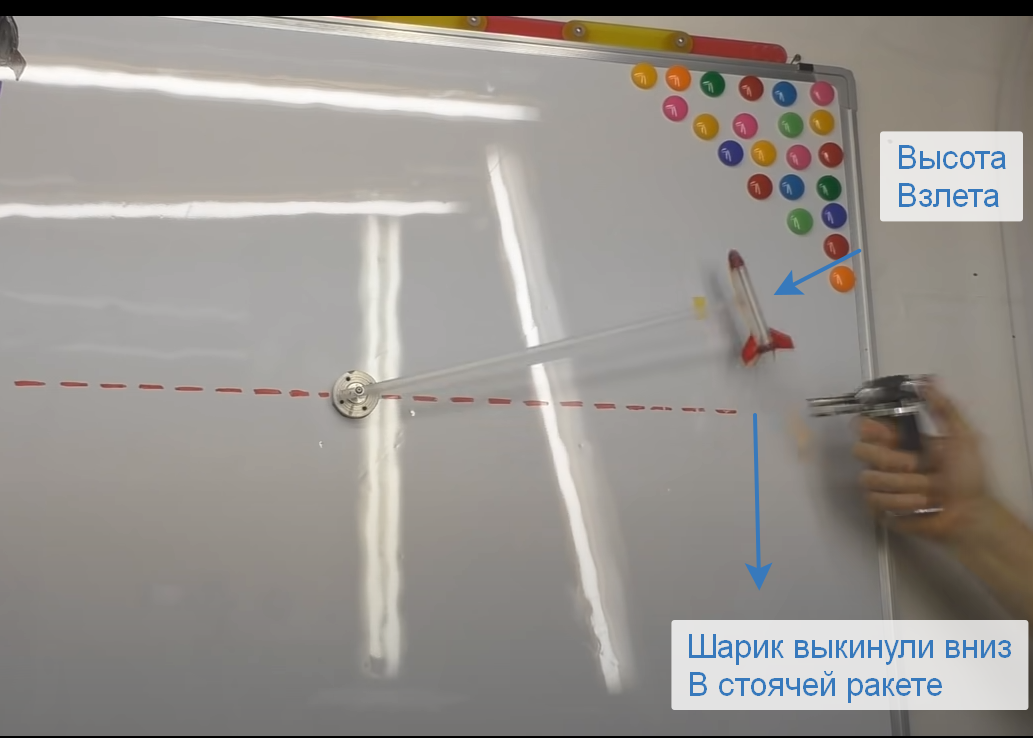
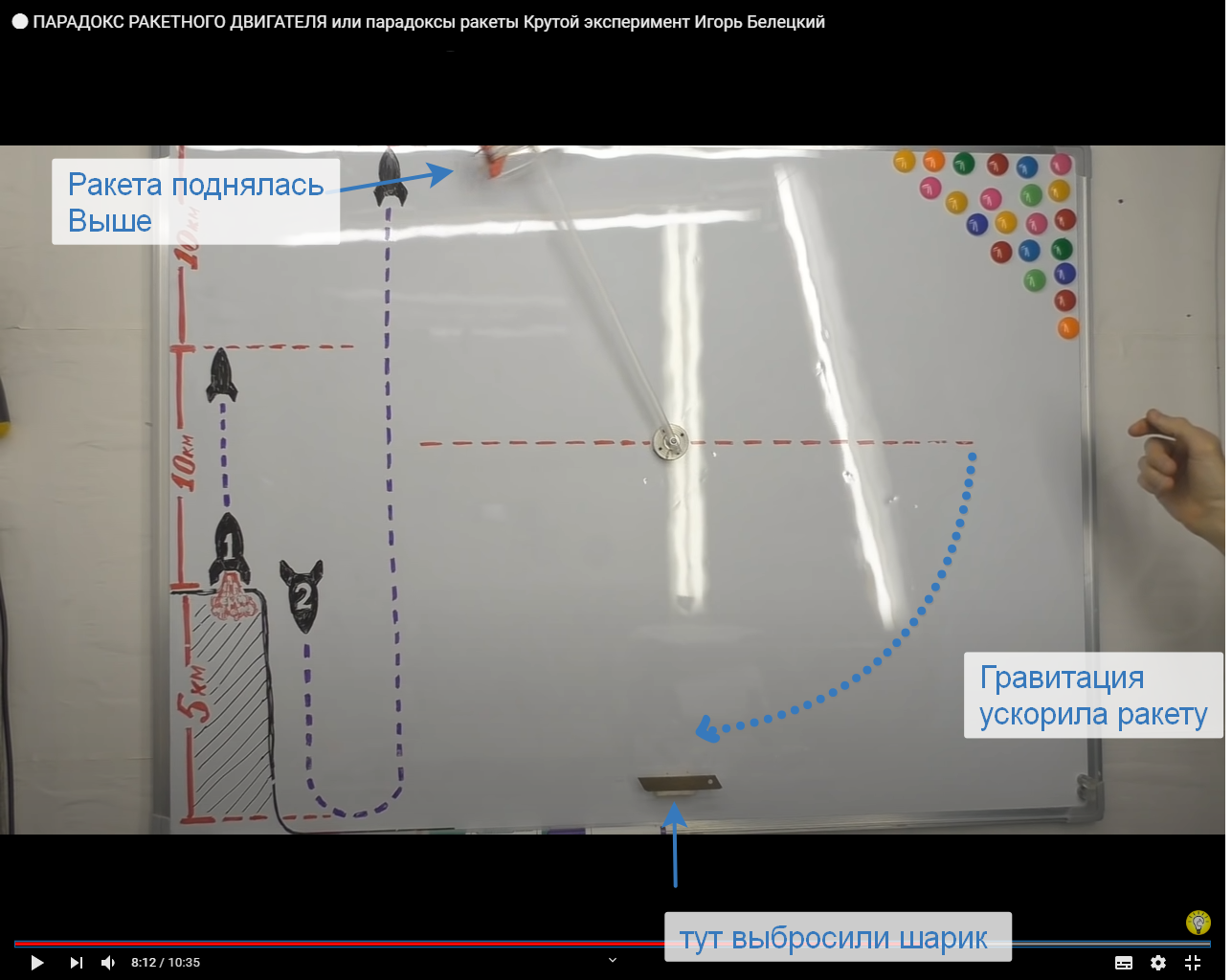
Source: chaîne YouTube d'Igor Beletsky

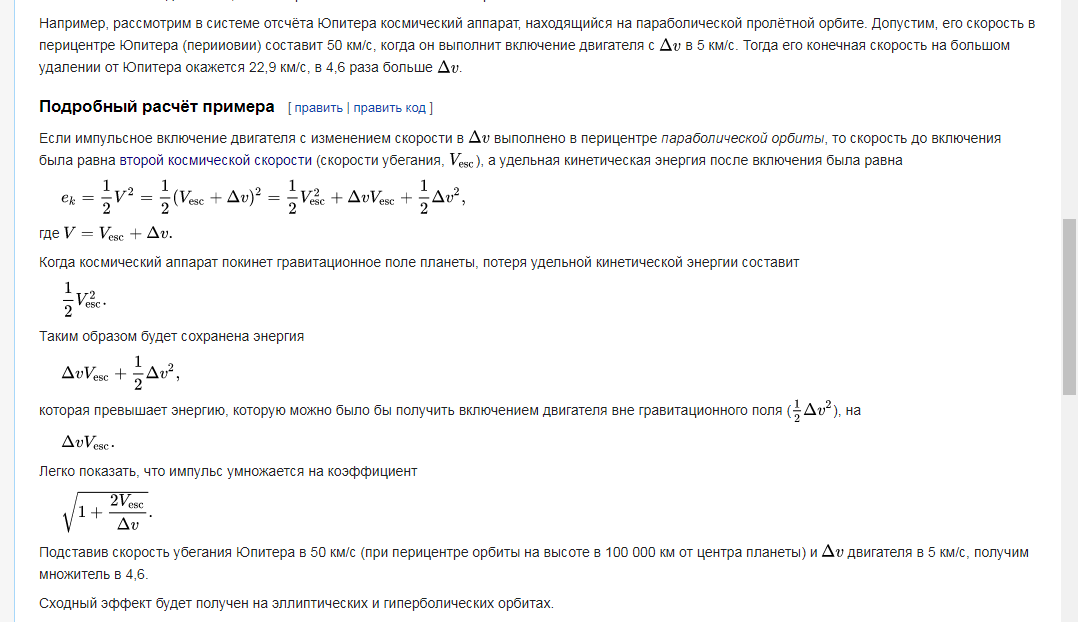
De Wikipedia

Dans une vidéo de YouTube - vous pouvez même voir cet effet de vos propres yeux, afin de comprendre pourquoi cela se produit, considérons séparément l'énergie cinétique et "thermique".



Tout ce que nous devons savoir sur l'énergie cinétique dans le contexte de la mécanique orbitale est la troisième loi de Newton: - La force d'action est égale à la force de réaction F = -F. Ceux. Si nous lançons quelque chose en avant à une vitesse de 10 m / s, alors quelque chose volera nécessairement dans la direction opposée avec la même vitesse de 10 m / s (avec les mêmes masses).



Et nous avons également besoin de la formule de l'énergie elle-même $$$E=\frac{mv^2}{{2}}$ (masse * vitesse au carré / 2), pour ne pas déranger avec une division constante par 2, je prendrai toujours une masse de 2 kg. - alors l'énergie sera juste égale à la vitesse au carré. Par exemple, à une vitesse de 10 m / s, l'énergie est de 10 * 10 = 100 Joules (pour chaque 2 kg.).



Alors imaginons un canon sur roues qui roule et nous allons accélérer le canon avec des coups. Nous prenons la masse des grains 2 kg. Il tire à une vitesse de +1 m / s (faible, bien sûr, mais il est pratique de compter). Disons que le pistolet roule à une vitesse de 2 m / s et tire dans la direction opposée - c'est-à-dire



Le noyau du canon avant le tir avait une vitesse de 2 m / s et son énergie était de 2 carrés = 4 joules, après le coup, sa vitesse est devenue 1 m / s et l'énergie était de 1 J. - c'est-à-dire qu'après le coup, le noyau a perdu 3 J et le canon en conséquence reçu cette énergie. Nous ne compterons pas la masse et la vitesse de l'arme, quelque chose d'autre est important pour nous.



Imaginez maintenant que le canon se déplace de 3 m / s, avant le tir le noyau a une énergie de 3 au carré = 9 J, et après le tir 2 au carré = 4 J, c'est-à-dire que cette fois le noyau a déjà perdu 5 joules, etc. plus la vitesse du canon est élevée, plus le noyau perd d'énergie. Alors la poudre à canon donne plus d'énergie? - Non, le gain d'énergie de chaque coup augmente, mais d'où vient la vitesse initiale du canon? À partir des mêmes plans, et pour que nous ayons 1 noyau à une vitesse de 4 m / s, nous devons tirer sur 5 noyaux à une vitesse inférieure (le numéro 5 vient du plafond, mais vous avez le sens) - c'est-à-dire qu'une énergie supplémentaire est prélevée sur les plans précédents. Voyons maintenant comment fonctionne la poudre à canon elle-même.

Comment la poudre à canon crée un élan

Bien que n'oublions pas son enfance de la pauvre Greta et prenons un panneau solaire catholique orthodoxe , chargez les batteries et considérez l'énergie sous une forme plus compréhensible pour une personne moderne. L'électricité est mesurée en Watts, et 1 Watt = 1 Joule (ils ont une signification physique différente, mais la ligne du bas est la même = accélération = pour accélérer 2kg. À 10m / s, 100 Watts = 100 J. sont nécessaires.) Maintenant, nous prenons une roue sphérique sous vide avec 2- avec des poids sur les bords, nous commençons à tourner avec un moteur électrique et jetons les poids dans différentes directions. Les poids sont, comme toujours, de 2 kg, la roue elle-même ne nous intéresse pas et nous ne considérerons l'énergie dépensée que pour détordre les poids. Roulons-les jusqu'à 10 m / s, pour cela, nous avons besoin de 10 * 10 = 100 W pour chaque charge.











Tout est simple ici, dépensé 200 watts = reçu 2 charges à une vitesse de 10 m / s dans des directions opposées. Ajoutons maintenant la vitesse à la roue elle-même = 10 m / s.







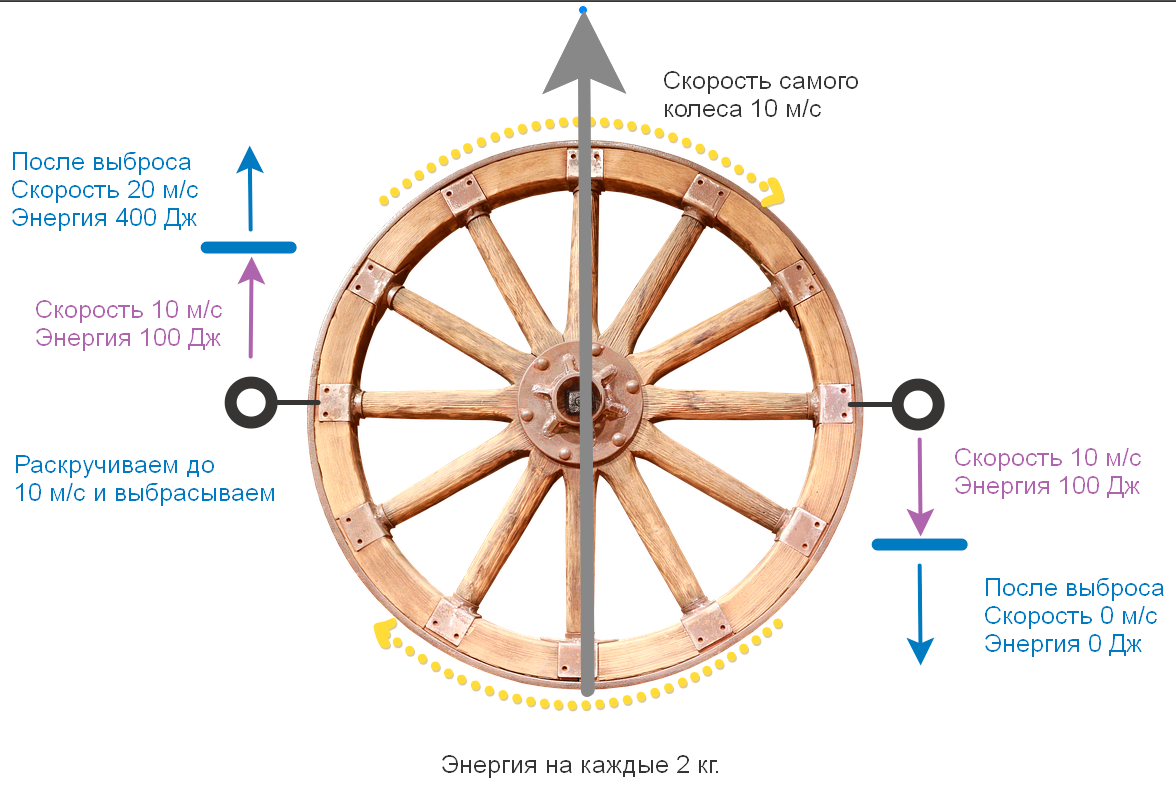
Et ici, nous voyons une image intéressante.



Pour se détendre, nous avons également dépensé 100 J pour chaque charge = 200 J. + 200 J. Chaque charge avait initialement (ils se déplaçaient tous les deux avec la roue de 10 m / s).



La charge accélérée a doublé sa vitesse et s'est envolée à une vitesse de 20 m / s, et son énergie a augmenté 4 fois - jusqu'à 400 J. - en fait, elle a emporté toute l'énergie en général - les deux +200 dépensés pour les détordre tous les deux, et l'énergie de la charge qui a ralenti - un autre +100 J. (+100 il avait au départ) - La loi de conservation de l'élan est une loi très impudente - l'accéléré prend tout. Au contraire, l'efficacité lors de l'accélération augmente de 50% à vitesse nulle à 100% à une vitesse d'éjection égale à la vitesse de la roue elle-même.



La même chose se produit dans une fusée qui brûle / éjecte du carburant à une vitesse d'environ 3000 m / s et avec l'accélération, l'efficacité du moteur augmente, mais pour entrer sur une orbite circulaire, une vitesse d'au moins 7900 m / s est nécessaire et voyons ce qui se passe si la vitesse de la roue elle-même est plus de taux d'éjection.







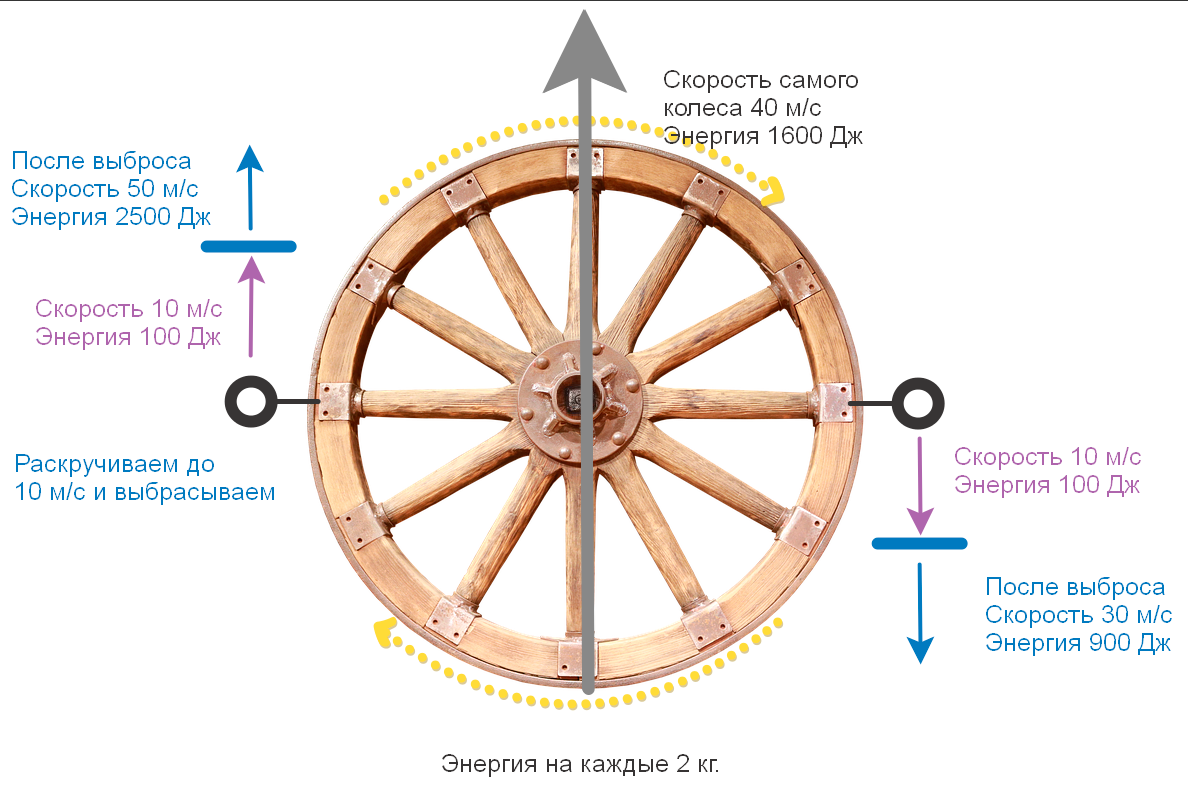
Ici nous avons à nouveau dépensé 200 J, et l'accéléré a augmenté son énergie de 1600 à 2500 = il a reçu 900 J = et il a de nouveau pris toute l'énergie dépensée pour dérouler 200 J et +700 J, que la charge qui a volé a perdu (1600-900 = 700) ... Parfois, ils disent que l'efficacité d'un moteur de fusée devient supérieure à 100%, mais vous devez comprendre que deux lois de conservation fonctionnent ici à la fois (la loi de conservation de l'énergie et la loi de conservation de l'élan). Nous les considérerons dans le cadre de la physique classique - dans laquelle l'impulsion est une propriété de l'espace (si nous jetons une pierre dans le vide et sans gravité à une vitesse de 10 m / s - alors elle ne s'arrêtera jamais et volera toujours à une vitesse de 10 m / s - donc cet espace est - pair, symétrique et sans frottement) - l'impulsion est décrite par trois lois de Newton.



Et l'énergie c'est…. l'enfer sait quoi, mais il est décrit par trois lois de la thermodynamique, on ne peut pas le comprendre sans entropie et le chat de Schrödinger - heureusement en mécanique orbitale on peut se passer de comprendre d'où vient l'énergie - on va la considérer comme une propriété de la matière - «l'essence brûle parce qu'elle essence ", et tout moteur de fusée a le paramètre suivant: Impulsion spécifique.







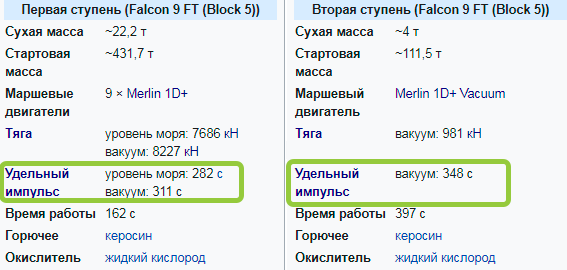
Nous multiplions ce nombre par 10 et nous obtenons la vitesse du carburant s'échappant de la buse - pour le deuxième étage du Falcon 9, elle est de 348 * 10 = 3480 m / s, à partir de ce paramètre, nous pouvons comprendre tout ce dont nous avons besoin. Et nous nous contenterons de la relativité de Laplace - quelle que soit la vitesse à laquelle nous jetons la masse - dans l'exemple avec une roue et 2 corps, les poids volent toujours à la même vitesse + -10 m / s par rapport à la roue elle-même, et dans le contexte d'une fusée c'est signifie que si 1 kg de carburant peut accélérer la fusée de 0 à 10 m / s, alors le même kilogramme de carburant peut accélérer la fusée de 10000 à 10010 m / s, malgré le fait que dans le second cas, la fusée en recevra mille fois plus d'énergie - c'est ce qu'on appelle l'effet Aubert.



Revenons maintenant au tout premier exemple de fusée de garage. Là, à la vitesse - l'efficacité du «moteur» de la balle était plus élevée, mais tout d'abord, la question était de la gravité - pour élever la balle à une hauteur, vous devez dépenser de l'énergie, et quand elle tombe, elle revient, et si nous mesurons la vitesse de la balle frappant le sol, alors dans le premier la balle est tombée d'une plus grande hauteur et a frappé plus fort, et dans la seconde d'une hauteur plus basse et a frappé plus faible - il a donné plus d'énergie, car il avait plus d'énergie au départ - il l'a reçue de l'expérimentateur qui l'a élevée à une hauteur et sur Terre de l'effet Oberth pour obtenir «Profit» est irréaliste.



Mais avec Jupiter, la situation est différente. J'ai écrit en détail sur la gravité et les vitesses cosmiques dans le dernier article, ici ce sera très court. Le fait est que la gravité ne donne pas / emporte de vitesse (km / s), mais de l'énergie (Joules). Et dans le cas de Jupiter, nous avons commencé à "tomber" dessus à une vitesse à peu près nulle, et à l'approche la plus proche, nous avons accéléré à 50 km / s (nous en avons reçu 2500 MJ d'énergie pour 2 kg), nous avons allumé les moteurs et accéléré à 55 km / s et notre énergie est devenue 55 * 55 = 3025 MJ, et quand nous avons volé "au-delà de la frontière" de sa gravité - il a repris non pas la vitesse (50 km / s), mais l'énergie qu'il nous a donnée (2500 MJ). il reste 3025-2500 = 525 MJ, pour obtenir la vitesse de l'énergie, nous extrayons la racine carrée = 22,9 km / s. Ici, nous avons eu exactement le "profit", car nous n'avons pas décollé de Jupiter et nous n'avons jamais eu une vitesse de 50 km / s.Il est très pratique de considérer la gravité comme une fosse.







Et dans le cas de Jupiter, nous avons en quelque sorte «tiré» le carburant d'une profondeur de 10 mille kilomètres (de la Terre), et l'avons laissé tomber à la «profondeur» de 200 mille kilomètres et nous avons volé hors de la fosse, et la majeure partie du combustible est restée dans la profondeur de cette fosse. (dans l'orbite de Jupiter), bien que nous aurions pu nous rapprocher du Soleil de la même manière et que l'effet aurait été encore plus grand - plus le corps massif est proche - plus la "profondeur" est grande. Par conséquent, lors des vols interplanétaires, l'effet Obert peut vraiment donner un "profit" et il est toujours utilisé, mais avant le départ de la Terre - toute l'énergie supplémentaire est tirée de la combustion des tonnes précédentes de carburant.

Formule de Tsiolkovsky

Puisque le carburant part toujours à la même vitesse = la fusée obtient la même accélération, la marge «vitesse» de la fusée peut être mesurée en km / s (vitesse caractéristique), par exemple, la vitesse caractéristique de 10 km / s signifie que la fusée peut accélérer de 0 à 10 km / s , ou accélérez d'abord de 6, puis décélérez de 1, et encore accélérez de 3 (pour un total de 10). Et la masse du carburant dépend directement de la vitesse à laquelle le carburant est éjecté de la buse (impulsion spécifique), puis la malédiction de Tsiolkovsky survient.

$$

$$V=I*ln(\frac{m_1}{{m_2}})$$

V-Vitesse finale de la fusée

I-Impulsion spécifique

M1- Masse initiale de la fusée avec carburant

M2- Masse finale de la fusée sans carburant



Si l'on prend une fusée d'une masse de 271 kg entièrement constituée de carburant et d'une impulsion spécifique de 3 km / s, alors avec une accélération de 0 à 3 km / s, la masse de carburant diminuera de 2,71 fois (nombre e) et nous aurons 271 / 2,71 = 100 kg de carburant, avec une accélération de 3 km / s, jusqu'à 6 km / s, la même chose se produira encore et ici il y aura à nouveau 2,71 fois moins de carburant 100 / 2,71 = 37 kg, et ainsi de suite. Puisque la conception de la fusée ne pèse pas 0 (généralement le poids de la structure est pris à 10%), alors nous pouvons prendre en toute sécurité le modificateur 3. Je vais laisser un exemple sous le spoiler.





Bien que nous ayons beaucoup simplifié, mais le nombre s'est avéré très proche de la réalité (idéalement, vous n'avez besoin que d'environ 18 km / s), et la fusée Saturn 5 qui transportait des singes parlants sur la Lune avait une masse de lancement de 3000 tonnes, et seulement 5 tonnes revenaient de la Lune. = 600 fois moins. Et cette fusée avait la taille d'un immeuble de 30 étages (110 m). En fait, il est presque impossible d'accélérer plus de 6 fois plus vite que l'impulsion spécifique. Bien que depuis 50 ans, ils promettent un moteur nucléaire avec une impulsion spécifique de 8 000 m / s, et avec un tel moteur, un vol vers la Lune et retour ne nécessiterait que 8 kg. carburant, mais jusqu'à présent, ce moteur reste de l'autre côté du téléviseur. Bien qu'en réalité encore pires, les propulseurs à haut RI accélèrent très longtemps et ne parviennent souvent même pas à surmonter l'accélération de la gravité sur Terre, et ils ne sont pas adaptés pour partir de la surface.et la plupart des horreurs se produisent au début.



Pour atteindre la hauteur de la lune, une vitesse de lancement de ~ 11 km / s est nécessaire, et le principal inconvénient des fusées est qu'elles n'accélèrent pas instantanément. Et bien que l'effet Oberth ne rapporte pas de profit sur Terre, il peut être complètement perdu, car en plus de l'impulsion spécifique, la fusée a un paramètre si important pour le lancement: la poussée.







Nous divisons les kilo Newtons en tonnes 7680/549 = ~ 14 m / s, et nous obtenons l'accélération de la fusée par seconde, et à la surface de la Terre l'accélération de la gravité est ~ 10 m / $$$^2$ , et si le moteur fonctionnait pendant 10 secondes dans le vide, nous accélérerions de 140 m / s (en excluant la diminution de la masse de la fusée), mais en raison de la gravité, nous avons accéléré de seulement 40 m / s, et l'efficacité du moteur dépend de la vitesse actuelle , et comme dans le cas d'une fusée de garage, lorsqu'elle a reçu plus d'énergie de la balle à une altitude inférieure, le processus inverse se produit pour une fusée qui décolle, et plus la fusée monte vite, plus l'énergie cinétique se transforme rapidement en énergie potentielle et moins elle donne de carburant, ou plutôt l'efficacité le moteur est toujours en croissance, mais pas aussi vite qu'il le pourrait si nous accélérions avec un minimum de montée. Par conséquent, plus la fusée est inclinée vers l'horizon, plus l'altitude augmente lentement et on obtient plus de l'effet Aubert. Mais ensuite on frotte contre l'atmosphère plus longtemps. Bien que l'atmosphère crée beaucoup moins de pertes,par rapport à l'avantage qui nous manque - le frottement crée de la température et nous avons besoin d'un bouclier thermique plus lourd qui devra éventuellement être mis en orbite. Mais ce n'est pas tout, après ~ 2 minutes ~ 75% du carburant brûle et la masse diminue de près de 4 fois, mais nous avons le même moteur et, comme il brûlait ~ 2,5 tonnes par seconde, il ne brûle que au début, il poussait ~ 600 tonnes avec une accélération de 14 m / s, et maintenant il pousse 150 tonnes avec une accélération de 14 * 4 = 56 m / s = les forces G sont multipliées par 4. Bien sûr, on peut réduire l'alimentation en carburant, mais alors les pertes gravitationnelles vont augmenter (ce sont les dernières secondes avant la séparation du premier étage). En fin de compte, tout cela conduit au fait que nous perdons environ la moitié du carburant pour ces pertes dites gravitationnelles (bien qu'il s'agisse plus probablement d'un profit perdu).Mais ce n'est pas tout, après ~ 2 minutes ~ 75% du carburant brûle et la masse diminue de près de 4 fois, mais nous avons le même moteur et, comme il brûlait ~ 2,5 tonnes par seconde, il ne brûle que au début, il poussait ~ 600 tonnes avec une accélération de 14 m / s, et maintenant il pousse 150 tonnes avec une accélération de 14 * 4 = 56 m / s = les forces G sont multipliées par 4. Bien sûr, on peut réduire l'alimentation en carburant, mais alors les pertes gravitationnelles vont augmenter (ce sont les dernières secondes avant la séparation du premier étage). En fin de compte, tout cela conduit au fait que nous perdons environ la moitié du carburant pour ces pertes dites gravitationnelles (bien qu'il s'agisse plus probablement d'un profit perdu).Mais ce n'est pas tout, après ~ 2 minutes ~ 75% du carburant brûle et la masse diminue de près de 4 fois, mais nous avons le même moteur et, comme il brûlait ~ 2,5 tonnes par seconde, il ne brûle que au début, il poussait ~ 600 tonnes avec une accélération de 14 m / s, et maintenant il pousse 150 tonnes avec une accélération de 14 * 4 = 56 m / s = les forces G sont multipliées par 4. Bien sûr, on peut réduire l'alimentation en carburant, mais alors les pertes gravitationnelles vont augmenter (ce sont les dernières secondes avant la séparation du premier étage). En fin de compte, tout cela conduit au fait que nous perdons environ la moitié du carburant pour ces pertes dites gravitationnelles (bien qu'il s'agisse plus probablement d'un profit perdu).seulement au début, il poussait ~ 600 tonnes avec une accélération de 14 m / s, et maintenant il pousse 150 tonnes avec une accélération de 14 * 4 = 56 m / s = les forces G sont multipliées par 4. Bien sûr, on peut réduire l'alimentation en carburant, mais alors les pertes gravitationnelles vont augmenter (ce sont les dernières secondes avant la séparation du premier étage). En fin de compte, tout cela conduit au fait que nous perdons environ la moitié du carburant pour ces pertes dites gravitationnelles (bien qu'il s'agisse plus probablement d'un profit perdu).seulement au début, il poussait ~ 600 tonnes avec une accélération de 14 m / s, et maintenant il pousse 150 tonnes avec une accélération de 14 * 4 = 56 m / s = les forces G sont multipliées par 4. Bien sûr, on peut réduire l'alimentation en carburant, mais alors les pertes gravitationnelles vont augmenter (ce sont les dernières secondes avant la séparation du premier étage). En fin de compte, tout cela conduit au fait que nous perdons environ la moitié du carburant pour ces pertes dites gravitationnelles (bien qu'il s'agisse plus probablement d'un profit perdu).que nous perdons environ la moitié du carburant pour ces soi-disant pertes gravitationnelles (bien qu'il s'agisse plutôt d'un profit perdu).que nous perdons environ la moitié du carburant pour ces soi-disant pertes gravitationnelles (bien que ce soit plutôt un profit perdu).



Puisque le carburant doit être jeté (brûlé) à une altitude minimale avec une accélération minimale vers le haut, les fusées sont d'abord accélérées à la première vitesse cosmique (~ 7,9 km / s pour la Terre) et placées sur l'orbite circulaire la plus basse (LEO 180-200 km) et absolument pas il est important que vous voliez vers la Lune / Mars ou l'OSG, vous devez d'abord passer au mouvement circulaire et arrêter de "discuter" avec la gravité.



Fuh, après avoir traversé toutes ces surcharges, pertes gravitationnelles, atmosphère enflammée et autres horreurs proches de la Terre - nous nous retrouvons sur une orbite de référence basse (LEO ~ 180 km). Disons que nous devons nous rendre sur une orbite géostationnaire (à une altitude d'environ 35 000 km). Vous avez probablement vu à plusieurs reprises la trajectoire la plus idiote de la transition entre les orbites dans les superproductions hollywoodiennes - lorsque la fusée est tournée verticalement et que les moteurs sont allumés contre la gravité. Dans l'orbite la plus basse, il n'y a que 200 km de la Terre - 3 fois moins que de Moscou à Saint-Pétersbourg !!! .. L'accélération de la chute libre à cette altitude n'est que de 5% de moins et s'élève à ~ 9,2 m / s par seconde. Nous tombons constamment, mais à cause de la vitesse d'avancement de 7,9 km / s, la terre ronde «glisse constamment sous nos pieds», donc même si nous tombons constamment, notre hauteur ne change pas. Et heureusementétant sur une orbite circulaire, nous ne pouvons qu'accélérer vers l'avant et la gravité n'interférera pas avec nous ...



Mais il existe une autre option, moins idiote par rapport à l'accélération, mais non moins idiote en général. Regardons ça aussi, donc, hennissement pur.



Nous avançons, accélérons vers le haut, la gravité va nous interférer, mais nous avons 3 dimensions !!! Nous pouvons accélérer sur le côté. Que va-t-il se passer?

Pour plus de commodité, prenons une vitesse de fusée de 8 km / s et une vitesse de décollage de carburant de 8 km / s, et voyons quelle sera la vitesse du carburant après le décollage.







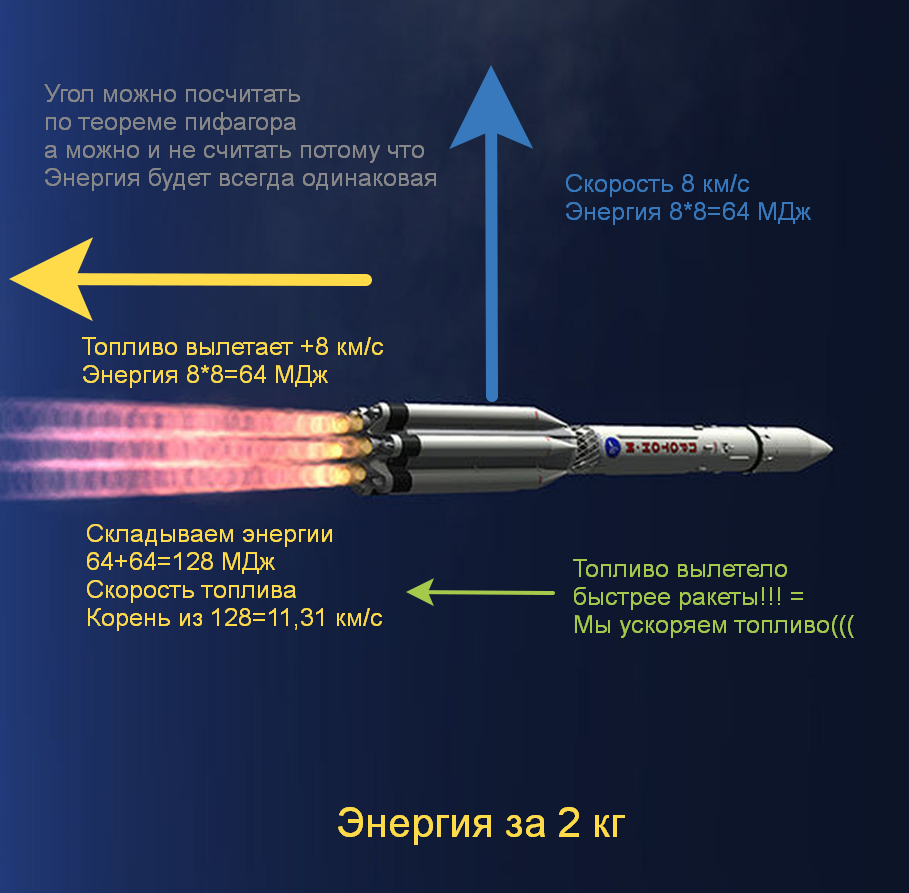
Donc, au départ, le carburant s'est déplacé de 8 km / s (64 MJ) vers l'avant avec la fusée, puis + 8 km / s (+64 MJ) s'est envolé vers la gauche par rapport à la fusée, et nous pouvons calculer l'angle (45 degrés) et dire que le carburant se déplace de 11,31. km / s par rapport à l'image et son énergie est de 128 MJ, ou on peut ne pas considérer l'angle et dire que le carburant se déplace de 8 km / s vers la gauche (64 MJ) et en même temps de 8 km / s vers le haut (64 MJ), mais son énergie est toujours de 128 MJ. Autrement dit, le carburant a accéléré de toute façon, mais nous allions accélérer la fusée ... Dieu, qu'est-il arrivé à la fusée!? At-il ralenti et est sur le point de tomber sur Terre?



Ne vous inquiétez pas, tout va bien avec la fusée - elle a également accéléré, et elle a accéléré du même 64 MJ, afin de calculer l'angle et la vitesse, vous devez connaître la différence de masses, mais autre chose est important pour nous. En fait, nous avons eu la même chose que dans le premier exemple avec la roue, quand elle ne bougeait pas et que nous avions 2 poids accélérés dans des directions opposées, ayant reçu la même énergie, et le rendement était alors de 50% - une surprise - l'effet Obert dépend non seulement de la vitesse, mais également à partir de la direction et cesse de fonctionner à tout écart par rapport au vecteur de vitesse actuel. Dans cet exemple, nous avons reçu 3 fois moins d'énergie que si nous jetions du carburant, et c'est avec une impulsion nucléaire de 8 km / s (à 3 km / s ~ 6 fois moins) - c'est ce qu'on appelle des pertes sur les manœuvres, et en fait, après être entré en orbite, il est presque impossible de tourner à gauche / droite et donc les fusées ne sont accélérées que vers l'avant,et si, en entrant en orbite, vous manquez au moins 30 degrés, alors il est moins coûteux de lancer une nouvelle fusée que de changer le vecteur vitesse de celle-ci. Heureusement, à l'ère du GPS et des ordinateurs, les fusées entrent en orbite avec une très grande précision et les pertes de manœuvre sont proches de zéro.

Comment grimper d'une hauteur de 200 km à une altitude de 35 000 km?

Compte tenu de tout ce qui précède, la seule direction d'accélération de la fusée est vers l'avant et perpendiculaire à la gravité.







Lors de l'accélération perpendiculaire à la gravité, l'altitude augmente du côté opposé de la planète (corps gravitant) et pour voler de l'orbite de référence basse (~ 200 km + vitesse ~ 8 km / s) à l'orbite géostationnaire (~ 35000 km + vitesse ~ 3 km / s ), nous devons accélérer à ~ 10,4 km / s (8 + 2,4), notre orbite circulaire deviendra elliptique et de l'autre côté nous monterons à une altitude de 35000 km, et notre vitesse sera de 1,7 km / s (à la gravité à distance prend de l'énergie). À ce stade, nous nous déplacerons à nouveau perpendiculairement à la gravité et nous devons accélérer à ~ 3 km / s, afin d'augmenter à nouveau l'altitude du côté opposé et de rendre notre orbite parfaitement ronde - Cela s'appelle le vol de Homan et c'est le moyen le moins cher de voyager dans l'espace - nous nous n'accélérons que vers l'avant et la gravité ne nous dérange jamais.



Les vols entre les planètes se font également le long de la même trajectoire, et comme vous l'avez peut-être déjà deviné, bien que la distance minimale entre la Terre et Mars soit de ~ 55 millions de kilomètres, cela n'affecte presque rien, car nous arriverons sur Mars depuis le côté opposé du Soleil après avoir dépassé environ 400 millions. km - c'est pourquoi le vol dure environ 8 mois.

Il est extrêmement difficile de réduire le temps de vol, ou plutôt de voler rapidement au large de la Terre, c'est facile et à une vitesse de départ de ~ 16,5 km / s nous atteindrons Mars dans 3 mois, mais à l'approche de celle-ci, nous n'aurons pas les mêmes vecteurs de vitesse. Pour faire simple, nous nous déplacerons de 1 km / s et Mars de 1 km / s, mais en même temps, nous volerons en avant, et Mars vers la gauche et nous aurons besoin d'une impulsion de freinage géante. Pour être plus précis, la différence de vitesse sera de 21 km / s, + il nous faut aussi 16,5 km / s pour un départ depuis la Terre = 37,5 km / s = la masse de la fusée vous-même.

?

Si votre grand-père était un reptilien aisé et vous a laissé un héritage de quelques tonnes d'antimatière, vous pouvez bien sûr voler vers Mars le long de n'importe quelle trajectoire à n'importe quelle vitesse (même tous les week-ends). Mais la pratique montre que la plupart des Reptiliens pauvres qui n'ont même pas d'argent pour leur propre soucoupe volante volent vers la Terre - avez-vous vu au moins un parking OVNI? - c'est tout - parce que les Reptiliens arrivent en taxi.



Il ne nous reste donc qu’un vol low-cost Homanovsky. Mais ne soyez pas pressé de désespérer - la mécanique orbitale est très paradoxale. Pourquoi pensez-vous qu'après le vol des humains vers la Lune, 4 rovers martiens ont été envoyés sur Mars en 50 ans, et un seul (puis chinois) a été envoyé sur le rover lunaire?





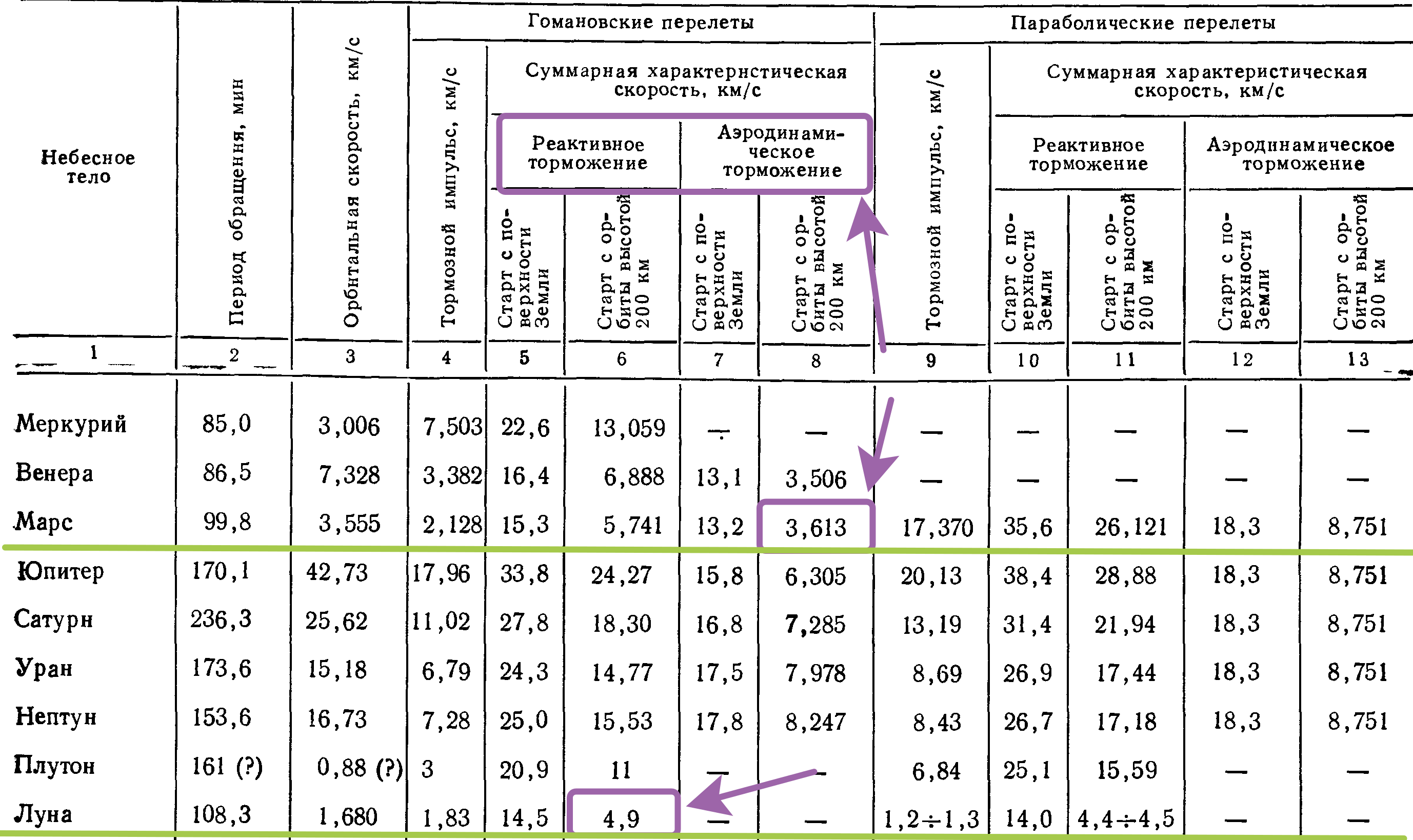
Tableau: V.I. Levantovsky La mécanique du vol spatial dans une présentation élémentaire.

Remarque: calculs de Levantovsky prenant en compte les pertes.



Et tout cela parce que pour atteindre la Lune, vous avez besoin d'une vitesse de départ de 11,1 km / s (je ne prend pas en compte les pertes - c'est une consommation idéale), et pour aller sur Mars, vous avez besoin d'une vitesse de départ de 11,5 km / s, seulement 0,4 km / s de plus, mais en même temps, les moteurs devront ralentir sur la Lune (1,83 km / s pour entrer sur l'orbite de la Lune et + 1,68 km / s pour atterrir sur la surface lunaire = 3,51 km / s), et sur Mars peut utiliser l'atmosphère pour freiner. Et en fait, il est moins cher de lancer un satellite sur l'orbite martienne que sur l'orbite lunaire !!! Je vous en dirai encore plus, pour lancer un satellite vers le GSO, nous avons besoin d'une impulsion de 10,4 km / s + puis d'un autre 1,3 = 11,7 km / s, et vers Mars 11,5 km / s (bien que vous devez prendre en compte que la protection thermique n'est pas pèse 0).

Bien sûr, cela ne s'applique pas aux humains, car dans 260 jours de vol vers Mars - les humains mangeront plus qu'une fusée, mais du point de vue de la cargaison, il est extrêmement surprenant - d'envoyer un tracteur sur l'orbite de Mars, moins cher que sur l'orbite de la Lune.



Il est peu probable qu'il soit possible d'atterrir complètement le tracteur à la surface de Mars (l'atmosphère est trop "vide"), mais néanmoins, la part du lion de la vitesse peut également être éteinte avec son aide, et l'atterrissage de marchandises sur Mars est également moins cher que sur la Lune (ou du moins comparable). L'atmosphère offre des possibilités incroyables.



Le retour de Mars est, bien sûr, beaucoup plus cher que de la Lune. Bien que si vous rêvez un peu et imaginez que nous pouvons complètement freiner sur l'atmosphère, alors il nous faut 11,5 km / s là-bas et 5,7 km / s retour = 17,2 km / s, et pour la Lune 11,1 là + 3, 51 * 2 (atterrissage / décollage) = 18,12 km / s - ~ 0,9 km / s de plus))). Mais les pertes gravitationnelles au départ de Mars seront plus que de la Lune, et une protection thermique est nécessaire, donc en réalité, cela s'avérera 3 à 5 fois plus cher (en termes de masse de carburant) pour le fret, et pour les singes, c'est même effrayant à imaginer.



Encore une fois, c'est si nous transportons du carburant pour revenir de la Terre. Si nous produisons du carburant sur le site d'atterrissage, la situation change radicalement et pour le départ de la Lune vers la Terre, nous avons besoin de 3,51 km / s (de Mars 5,7) - Le carburant lunaire est moins cher que le carburant martien, mais l'atterrissage sur Mars est moins cher et il est plus facile pour nous de construire la production elle-même, et la malédiction de Tsiolkovsky est une chose très terrible, et même en économisant 1 km / s à l'atterrissage, nous pouvons envoyer 1,5 fois plus de charge utile.



Étonnamment, la colonisation de Mars présente même des avantages par rapport à la Lune. Et la Lune elle-même est plus facile à coloniser depuis Mars que depuis la Terre. Terre-Lune 11,1 km / s et Mars-Lune 5,7 km / s. Et s'il y avait aussi de la vie sur Mars, ils auraient colonisé notre Lune il y a longtemps.



La mécanique orbitale est paradoxale - la gravité crée un «relief» et le système solaire n'est en fait pas le même que celui que l'on peut voir dans un télescope. Dans le prochain article, nous examinerons ce «soulagement» plus en détail et essayerons de trouver la réponse à la question - où se trouve le carburant le moins cher du système solaire. Et pour comprendre ce «relief», nous n'avons besoin que de la formule de Tsiolkovsky et de la deuxième vitesse spatiale (assurez-vous de lire le dernier article sur les vitesses spatiales). Et tout cela avec les exemples les plus simples.



Ceux qui ont lu le dernier article savent que j'ai un Reptiloid familier, et après le cinquième verre du Nouvel An, il me l'a dit! Il dit qu'ils ont la technologie qu'ils utilisent pour changer les orbites de planètes entières. Ils prennent d'abord "Jupiter" et quelques petits "Pluton", abaissent leurs orbites plus près du "Soleil", mais "Pluton" tourne dans la direction opposée et entre en collision frontale avec le "Jupiter" à une vitesse de 600 km / s chacun, et bien que Jupiter est 20000 fois plus lourd que Pluton, mais en raison de l'énorme vitesse de collision, il chauffe jusqu'à plusieurs milliers de degrés et commence à briller comme une ampoule. Et puis ils jettent cette "ampoule" de leur système stellaire à un autre à une vitesse de 200 à 300 km / s. Oui, le vol prend beaucoup de temps - plusieurs milliers d'années, mais ils se déplacent confortablement - avec un mini "Sun" (il se refroidit très longtemps).Ensuite, ils volent vers l'étoile désirée, déploient leur groupe de soucoupes volantes et renvoient toutes les planètes vers leur étoile d'origine. Et ils ont déjà rassemblé plusieurs milliers de planètes - ils n'ont déjà nulle part où les garer. Ils ont même aveuglé 80 "Jupiters" en 1 et allumé le deuxième "Soleil".



Il ne m'a pas encore dit comment ces soucoupes volent, mais il a déjà dit beaucoup d'autres choses, alors assurez-vous de vous abonner à la chaîne - il y aura des technologies OVNI plus loin.



Eh bien, assurez-vous de republier, ou aimez-vous vraiment ce qui se passe avec Internet? Quand vous entrez dans les tendances YouTube - et là, en haut de la vidéo, Vlad est baigné de ... chips de papier. Vous ne comprenez pas pourquoi cela se produit? - et tout cela parce que les écoliers font des repostages - et vous ne le faites pas !!! Comme le disait Confucius dans sa lettre à Aristote: - Quiconque ne veut pas se republier - lira ce que les écoliers republient!







Que voulez-vous comme sur YouTube américain? - le republication est le devoir sacré de tout internaute! Par conséquent, ne laissez pas le papier Vlad dégrader Internet !!! Pour votre bien et pour les générations futures - republiez!



Le dernier article sur les vitesses cosmiques et la gravité .



Parfois, entre les états, je ne suis ni vivant ni mort - je m'effondre sur secousse .