Quand j'étudiais à l'institut, je n'aimais vraiment pas la philosophie. Le fait n'est pas seulement qu'à cette époque, c'était une philosophie marsiste-léniniste - je n'ai tout simplement pas vu l'intérêt de ce fouillis insensé de mots. Bien plus tard, j'ai découvert que j'aimais précisément la philosophie - mais la philosophie des sciences.
À mon avis, la philosophie devrait avoir un objet de considération spécifique: les infinis en théorie des ensembles, les nombres transfinis, les théories et la prouvabilité, l'hypothèse de Max Tegmark sur l'univers mathématique. Et puis il y a un réel progrès (par exemple, le théorème de Gödel), et les mots correspondent juste au cadre donné par les spécificités. Sinon, il s'agit d'une tentative de construire une structure à partir de semoule liquide, une sorte de masturbation intellectuelle.
Georg Cantor, qui a jeté les bases de la théorie des ensembles et découvert la différence entre les types de cardinalités (en anglais, cardinalities), est, à mon avis, un philosophe bien plus grand que Kant et Hegel. Vous ne pouvez pas retirer une cuillère de votre tasse de café lorsque vous le buvez et mangez une pomme avec un talon, mais vous devez connaître la différence entre un ensemble dénombrable et un continuum si vous êtes impliqué dans l'informatique ou tout autre domaine technique.
L'une des choses philosophiquement intéressantes est le fameux Axiome of Choice (AC) - extérieurement totalement inoffensif, mais avec des conséquences monstrueuses. L'axiome déclare que s'il y a deux ensembles non vides, alors il y a aussi un ensemble contenant exactement un élément des deux:
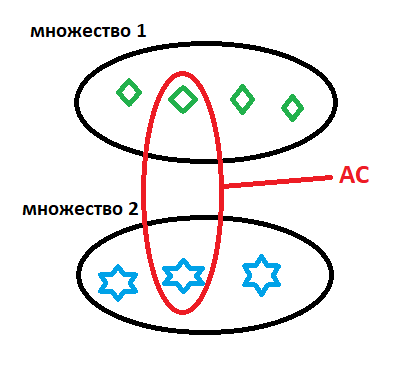
Si l'un de ces ensembles ne contient qu'un seul élément, il sera toujours sélectionné et fonctionnera comme un hook, "récupérant" des éléments du deuxième ensemble. Si après chaque acte de choix, nous supprimons les éléments sélectionnés, alors en utilisant cette procédure, nous pouvons analyser tout ensemble par éléments .
Paradoxes Axiomes de choix
, "" , " ". , , ( ). , (, ) . .

, - ! ? . , , - . , . !
, . , , . AC , . , , . "" AC (, ), , , .
- , , . , , . . , , . - .
, [0,1]. , , , '0.324443', '1/3', '1/pi' (pi ), 'min ...' ( , ). , , ... , , . , , !
, , :
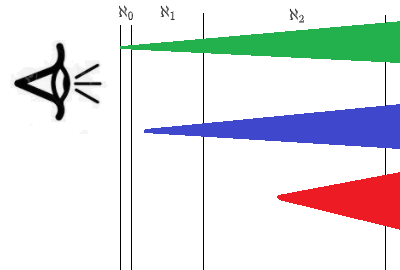
( ), . ' ' . - ( ) ( - ). ( , ?) - !
:

. -! , , , . :

, . , ?
, , ,
, (
)
- 'one level up' :
,
. ,
. , .
, /
. - - , . . (one level down) ' , ' , ( )
() , . . , , , , , . , , , , '' .
Cognitive Closure
. , :
- , . . , . ( ? , )
, cognitive closure - fixed points. . 1,2,3, ... 5556054, , . . , ' ' - , , .
Il est important que la fermeture cognitive ne soit pas visible d'en bas comme une frontière. Ce n'est pas un obstacle. Ce n'est pas une tâche difficile que vous ne pouvez pas résoudre. Vous ne le voyez pas du tout - tout va bien, vous pouvez écrire un autre article , enquêter sur un autre phénomène , prouver un théorème de plus . Personne ne vous arrêtera - vous ne pouvez tout simplement pas comprendre ce que vous ne pouvez pas comprendre. Vous ne verrez pas le problème.