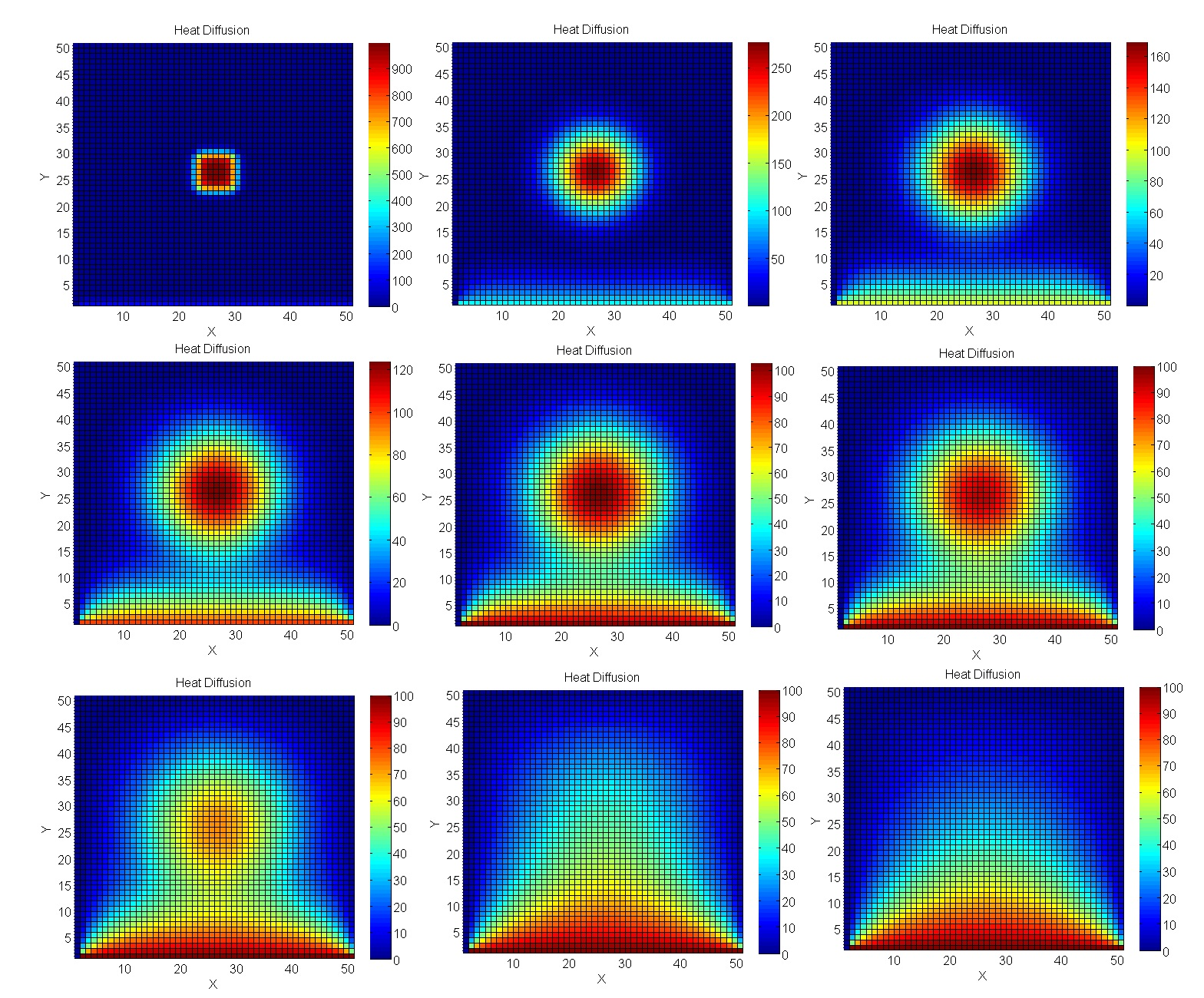

Chauffons des plaques métalliques sur le GPU
Tout le monde sait que Python ne brille pas avec la vitesse par lui-même. À mon avis, le langage est excellent dans sa lisibilité, mais le créneau principal de son application est celui où vous attendez la plupart du temps des entrées / sorties de données. Par convention, vous pouvez écrire du code super performant en Rust ou C, mais 99% du temps, il attendra.
Cependant, Python est également excellent en tant que colle syntaxique de haut niveau. Dans ce cas, sa partie interprétée tranquillement appelle du code à grande vitesse écrit dans des langages de programmation compilés. En règle générale, les bibliothèques traditionnelles telles que NumPy sont utilisées pour cela.
Mais nous allons aller un peu plus loin, essayer de paralléliser les calculs dans CUDA et utiliser un hybride étrange mais fonctionnel de C ++, stdpar et le compilateur nvc ++ de Nvidia. Eh bien, en même temps, essayons d'évaluer les performances. Prenons deux problèmes: le tri des nombres et la méthode Jacobi, que nous allons utiliser pour calculer l'échauffement d'une plaque métallique.
Appeler C ++ depuis Python
Notre code de tri ressemblera à ceci:
# distutils: language=c++
from libcpp.algorithm cimport sort
def cppsort(int[:] x):
sort(&x[0], &x[-1] + 1)
Dans la première ligne, nous indiquons explicitement que Cython doit utiliser C ++, et non le C. par défaut. Dans la seconde, nous importons la fonction de tri depuis C ++, puis la logique elle-même suit. Placez le code dans le fichier cppsort.pyx. Notez que l'extension est différente du py habituel, car nous allons le compiler ou exécuter cythonize dans la terminologie Cython.
La compilation peut être effectuée manuellement ou incluse dans setup.py, où nous décrivons entièrement la préparation de notre environnement.
Dans setup.py, cela ressemble à ceci:
from setuptools import setup
from Cython.Build import cythonize
setup(
ext_modules = cythonize("cppsort.pyx")
)
Mais nous pouvons simplement le faire sur la ligne de commande:
cythonize -i cppsort.pyx
Sous le capot, quelque chose comme ça va se passer:

- Cython traduira le code python en C ++ et générera un cppsort.cpp valide.
- Le compilateur C ++ (dans ce cas g ++) compile le code C ++ dans le module d'extension Python
- Le module d'extension Python est importé dans le code en tant que module Python normal.
Après compilation, nous pouvons importer et tester immédiatement le tri:
from cppsort import cppsort
import numpy as np
x = np.array([4, 3, 2, 1], dtype="int32")
print(x)
cppsort(x)
print(x)
Le tableau [4, 3, 2, 1] est trié avec succès dans [1, 2, 3, 4] en utilisant C ++ std :: sort.
Allons au GPU?
Les algorithmes de bibliothèque standard C ++ peuvent être appelés avec l'argument de stratégie d'exécution parallèle . Cet argument indique au compilateur que vous souhaitez diviser l'algorithme en processus parallèles.
Cela étant dit, C ++ a plusieurs options pour cette stratégie:
- std :: execution :: seq: exécution séquentielle. Le parallélisme est interdit.
- std :: execution :: unseq: exécution vectorisée dans le thread appelant.
- std :: execution :: par: Exécution parallèle sur un ou plusieurs threads.
- std :: execution :: par_unseq: exécution parallèle sur un ou plusieurs threads. Chaque flux sera vectorisé chaque fois que possible.
Dans ce cas, vous devez vous-même surveiller la condition de concurrence et l'impasse. Le compilateur standard g ++ essaiera de distribuer le calcul sur les cœurs de CPU. Mais nous pouvons prendre un compilateur propriétaire de Nvidia - nvc ++ et lui donner l'option "-stdpar". stdpar est le parallélisme standard C ++ de Nvidia avec exécution de code parallèle sur le GPU.
Réécrivons le code, en tenant compte de la nécessité de créer une copie locale du tableau, puisque le GPU ne pourra pas accéder au tableau situé dans NumPy.
from libcpp.algorithm cimport sort, copy_n
from libcpp.vector cimport vector
from libcpp.execution cimport par
def cppsort(int[:] x):
cdef vector[int] temp
temp.resize(len(x))
copy_n(&x[0], len(x), temp.begin())
sort(par, temp.begin(), temp.end())
copy_n(temp.begin(), len(x), &x[0])

Maintenant, cela doit être compilé à nouveau, mais en utilisant nvc ++. Cette fois, écrivons un setup.py normal et appelons-le:
CC=nvc++ python setup.py build_ext --inplace
Nous importons dans le code et essayons d'appeler:
x = np.array([4, 3, 2, 1], dtype="int32")
cppsort(x) # GPU
Performance
Traditionnellement, les GPU sont bons là où il y a beaucoup du même type de calcul léger. Les tâches lourdes, les tâches GPU uniques ne fonctionneront pas. De plus, cela vaut la peine de considérer le volume de vos données. Si vous avez peu de données, vous obtiendrez une surcharge importante pour le processus de parallélisation, les E / S entre le CPU et le GPU. En conséquence, ce code fonctionnera très probablement plus efficacement sur un processeur nu, parfois même dans un seul cœur, s'il y a très peu de données. Mais sur les grandes baies, le GPU sera certainement en avance.
Il y a une excellente comparaison de tri ici. La vitesse NumPy a été prise comme une unité, puis la multiplicité de l'augmentation de vitesse dans chaque méthode a été calculée par rapport à elle.
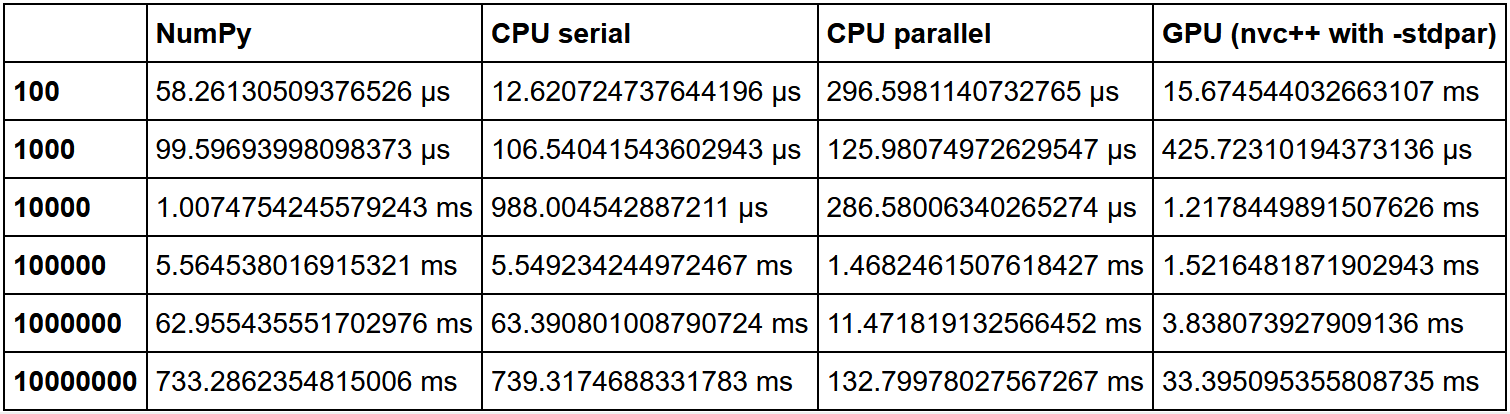
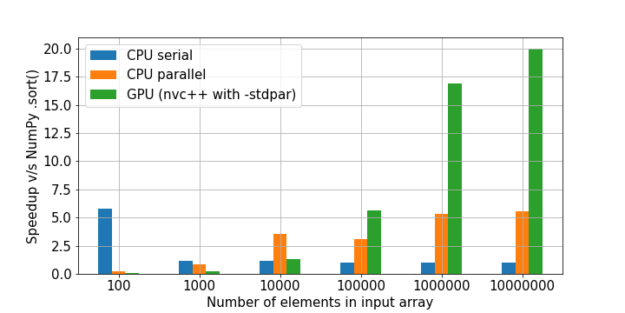
Comme on peut le voir, l'hypothèse selon laquelle le gain d'utilisation du GPU sur une grande quantité de données est en augmentation est confirmée.
Nous calculons le chauffage de la plaque
Prenons un problème plus proche de la modélisation d'ingénierie réelle - les calculs utilisant la méthode Jacobi. En particulier, ils sont excellents pour le calcul des processus de température dans l'espace 2D.

Code de simulation
"""
simulates heat equation on rectangle returning a heat map at a number of times
boundary and initial conditions are 0, source represents burner on a stove
This program is based on the script FEniCS tutorial demo program: Diffusion of a Gaussian hill.
u'= Laplace(u) + f in a square domain
u = u_D = 0 on the boundary
u = u_0 = 0 at t = 0
u_D = f = stove burner flame
This program succesfully runs in the fenics docker image, see the book Solving PDEs in Python.
to animate: convert -delay 4 -loop 100 heatequation10*.png heatstovelinn.gif
to crop:convert heatstovelinn.gif -coalesce -repage 0x0 -crop 810x810+95+15 +repage heatstovelin.gif
"""
from fenics import *
import time
import matplotlib.pyplot as plt
from matplotlib import cm
# Create mesh and define function space
nx = ny = 100
mesh = RectangleMesh(Point(-2, -2), Point(2, 2), nx, ny)
V = FunctionSpace(mesh, 'P', 1)
# Define boundary, source, initial
def boundary(x, on_boundary):
return on_boundary
bc = DirichletBC(V, Constant(0), boundary)
u_0 = interpolate(Constant(0), V)
f = Expression('exp(-sqrt(pow((a*pow(x[0], 2) + a*pow(x[1], 2)-a*1),2)))', degree=2, a=5) #steep guassian centred on the unit sphere
final_time = 0.035
num_pics = 72
for i in range(num_pics):
T = final_time*(i+1.0)/(num_pics+1) #solve time even space
#T = final_time*1.1**(i-num_pics+1) #solve time log space
num_steps = 30
dt = T / num_steps # time step size
# Define variational problem
u = TrialFunction(V)
v = TestFunction(V)
F = u*v*dx + dt*dot(grad(u), grad(v))*dx - (u_0 + dt*f)*v*dx
a, L = lhs(F), rhs(F)
# Time-stepping
u = Function(V)
t = 0
for n in range(num_steps):
t += dt #step
solve(a == L, u, bc) #solve
u_0.assign(u) #update
#plot solution
plot(u,cmap=cm.hot,vmin=0,vmax=0.07)
plt.axis('off')
plt.savefig('heatequation10%s.png'%(i+10),figsize=(8, 8), dpi=220,bbox_inches='tight', pad_inches=0,transparent=True)
Écrivons un solveur similaire en Cython pour une compilation ultérieure à l'aide de CUDA:
# distutils: language=c++
# cython: cdivision=True
from libcpp.algorithm cimport swap
from libcpp.vector cimport vector
from libcpp cimport bool, float
from libc.math cimport fabs
from algorithm cimport for_each, any_of, copy
from execution cimport par, seq
cdef cppclass avg:
float *T1
float *T2
int M, N
avg(float* T1, float *T2, int M, int N):
this.T1, this.T2, this.M, this.N = T1, T2, M, N
inline void call "operator()"(int i):
if (i % this.N != 0 and i % this.N != this.N-1):
this.T2[i] = (
this.T1[i-this.N] + this.T1[i+this.N] + this.T1[i-1] + this.T1[i+1]) / 4.0
cdef cppclass converged:
float *T1
float *T2
float max_diff
converged(float* T1, float *T2, float max_diff):
this.T1, this.T2, this.max_diff = T1, T2, max_diff
inline bool call "operator()"(int i):
return fabs(this.T2[i] - this.T1[i]) > this.max_diff
def jacobi_solver(float[:, :] data, float max_diff, int max_iter=10_000):
M, N = data.shape[0], data.shape[1]
cdef vector[float] local
cdef vector[float] temp
local.resize(M*N)
temp.resize(M*N)
cdef vector[int] indices = range(N+1, (M-1)*N-1)
copy(seq, &data[0, 0], &data[-1, -1], local.begin())
copy(par, local.begin(), local.end(), temp.begin())
cdef int iterations = 0
cdef float* T1 = local.data()
cdef float* T2 = temp.data()
keep_going = True
while keep_going and iterations < max_iter:
iterations += 1
for_each(par, indices.begin(), indices.end(), avg(T1, T2, M, N))
keep_going = any_of(par, indices.begin(), indices.end(), converged(T1, T2, max_diff))
swap(T1, T2)
if (T2 == local.data()):
copy(seq, local.begin(), local.end(), &data[0, 0])
else:
copy(seq, temp.begin(), temp.end(), &data[0, 0])
return iterations
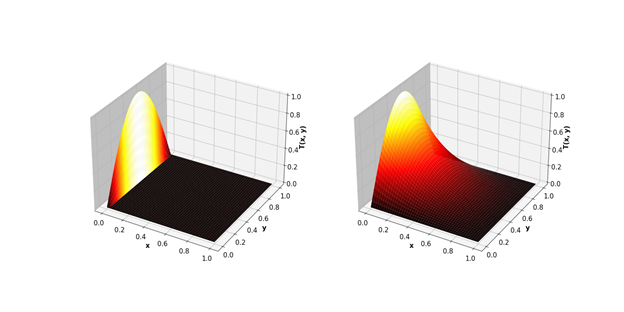

En conséquence, l'écart GPU est encore plus important.
Moins
- L'écriture de ce type de code est un peu plus compliquée qu'une version pure de Python et nécessite une compréhension du fonctionnement du calcul parallèle sur un GPU.
- Il est nécessaire de copier les données dans une matrice distincte pour les transférer vers le GPU, où la carte vidéo n'a pas accès. Cela peut être un problème lorsqu'il s'agit de très grands tableaux.
