
Un article sur le calcul de la distance au Soleil a suscité un autre texte - sur le calcul de la distance à la Lune (puisque ce chiffre a été utilisé par Aristarque dans ses calculs, la question s'est posée, d'où l'a-t-il obtenu). Mais déjà dans les commentaires du deuxième texte, la question suivante a été posée - "Et maintenant, pouvez-vous nous en dire plus sur le rayon de la Terre?"
Demandé - nous répondons. Eh bien, pour ne pas "me lever deux fois", je ne commencerai même pas par le rayon, mais par la façon dont les Grecs sont arrivés à la conclusion que la Terre a la forme d'une boule, pas d'un disque ou d'un coffre (comme l'a soutenu plus tard le scientifique byzantin Kozma Indikoplov).
Ce sont les Grecs qui se sont occupés de cette question, dans les civilisations plus anciennes (Babylone, Egypte), ils ont étudié le ciel, et assez soigneusement, ont essayé de prédire le mouvement des corps célestes, mais ils ne se sont pas préoccupés de la question de la forme de la Terre.
Il est difficile de dire lequel des Grecs a été le premier à exprimer l'idée que la Terre est une boule, la version la plus courante est celle de Pythagore . Mais le plus ancien traité écrit avec cette déclaration qui nous soit parvenu («Sur une sphère en mouvement») appartient à un autre mathématicien - Autolycus de Pitana, né deux cents ans plus tard que Pythagore. Certes, c'est généralement le plus ancien traité de mathématiques ancien qui nous soit parvenu. Et déjà dedans, la Terre s'appelle une sphère. Mais là, il était présenté comme un donné, c'est-à-dire Autolycus n'a pas été le premier à proposer cette idée.
Et puis son contemporain le grand Aristote, dans son traité du Ciel, a étayé cette affirmation en détail . Au fond, les explications étaient de nature philosophique (la Terre sphérique est le centre indestructible du cosmos, etc.). Mais il y avait aussi un certain nombre de preuves très spécifiques. Tout d'abord, les résultats des observations d'éclipses lunaires: ils ont toujours une ligne de démarcation arquée. «Puisque la Lune est éclipsée parce qu'elle est obscurcie par la Terre, alors la raison de cette forme est la circonférence de la Terre, et la Terre est sphérique», conclut Aristote.
Il a tiré une conclusion encore plus intéressante de ses observations des étoiles. Pour commencer, le philosophe a noté qu'en Egypte et en Macédoine, il existe des différences perceptibles pour l'observateur dans la disposition des étoiles. Et il en déduit: "De là, il est clair non seulement que la Terre est ronde, mais aussi que cette sphère est petite: sinon, de tels déplacements insignifiants ne provoqueraient pas de changements aussi rapides."
Eh bien, puisque la partie instruite des Grecs a décidé de la forme de la Terre, ainsi que du fait que ses dimensions ne sont pas si grandes, la prochaine étape s'est suggérée - mesurer la Terre.
Avant de passer au processus et à ses résultats, je voudrais noter une nuance. Les Grecs ont mesuré, comme je l'ai dit par étapes, mais la nuance est que c'est maintenant un kilomètre et un kilomètre en Afrique. Et puis il n'y avait pas de système SI. Chaque étape fait 100 paires de pas ou 600 pieds, mais les étapes et les pieds dans différents systèmes de mesures pouvaient légèrement différer: il y avait plusieurs options pour les étapes, de 172 à 185 mètres (et aussi la version babylonienne de la scène, mais cela ne nous intéresse pas ici). Vous devez souvent deviner à quelle étape tel ou tel auteur a utilisé. Par conséquent, lorsque nous traduisons les résultats en kilomètres habituels, nous courons bien sûr le risque de faire des erreurs. Mais - dans les 6-7%. Pour l'astronomie c'est beaucoup, pour l'histoire de la question c'est tolérable.
Maintenant, en fait sur la façon dont les Grecs mesuraient la Terre. Deux études sont connues à cet effet. La première a été réalisée par Ératosthène au IIIe siècle avant JC, la seconde - par Posidonius un peu plus de cent ans plus tard. Dans les deux cas, les Grecs ont adopté une approche similaire, la différence résidait dans les détails. Sa signification est la suivante: le Soleil et les étoiles sont disponibles pour une observation simultanée à différents endroits sur Terre, mais comme la distance qui les sépare est clairement plusieurs fois plus grande que les dimensions de la Terre elle-même, nous pouvons considérer tous les rayons de lumière venant d'eux vers nous parallèles.
Ératosthène a mesuré la hauteur du Soleil au-dessus de l'horizon à midi du solstice d'été à Alexandrie et Sienne (Assouan). Pourquoi là-bas? Et même avant lui, les anciens Égyptiens ont remarqué que pendant le solstice d'été, le soleil illumine le fond des puits profonds de Sienne (aujourd'hui Assouan), mais pas à Alexandrie. Si la Terre était plate, raisonna Eratosthène, cela ne pourrait pas être (nous nous en souvenons - les rayons sont parallèles), mais elle est ronde, c'est-à-dire incurvé. Et Sienne et Alexandrie sont sur le même méridien (croyait-il) à une distance de 5000 stades l'une de l'autre. Cela signifie que les murs d'Alexandrie sont inclinés à un certain angle par rapport aux murs de Sienne, de sorte qu'à midi du solstice, ils continuent à projeter de l'ombre.
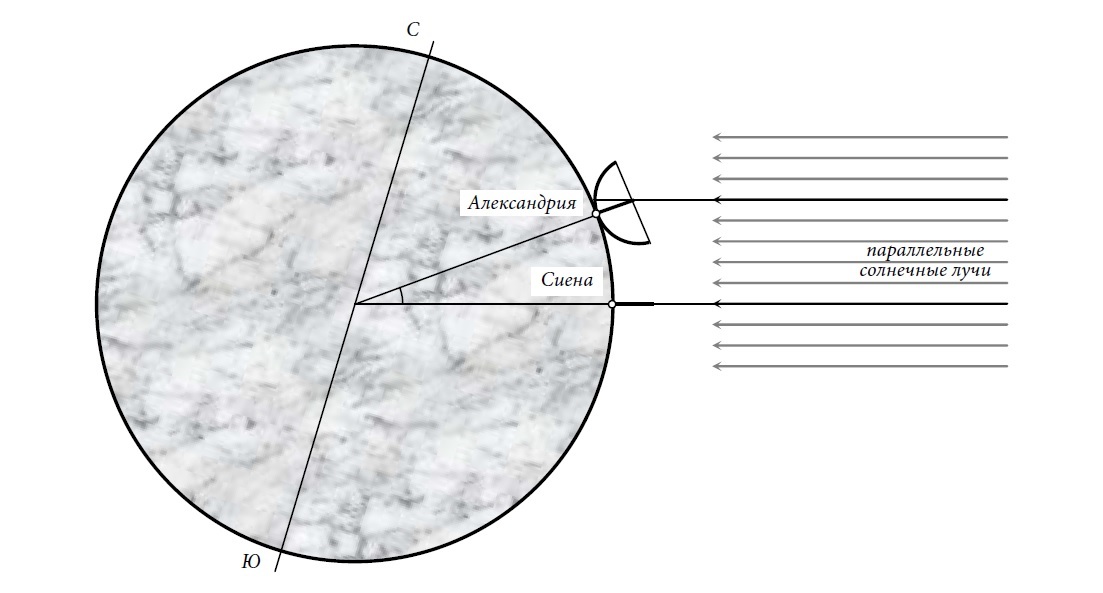
Ératosthène mesura l'ombre de l'un des obélisques d'Alexandrie, connaissant également sa hauteur, il «construisit un triangle à partir de l'obélisque et de son ombre» et calcula que l'angle de déviation de l'obélisque par rapport au rayon du soleil était d'un peu plus de 7 degrés. Cela signifiait qu'Alexandrie était à 7 degrés de Sienne sur la circonférence de la terre. Un tel angle est 1/50 d'un cercle et en même temps les 5000 stades mentionnés. D'où la circonférence totale de 250 000 stades, conclut Ératosthène. Et les Grecs savaient calculer le rayon, connaissant la circonférence.
Aujourd'hui on sait que les calculs d'Eratosthène comportaient un certain nombre d'erreurs graves: Alexandrie et Sienne ne sont pas situées sur le même méridien, donc la différence entre leurs parallèles est moindre, cette distance elle-même a également été mesurée approximativement, selon les hommes de la caravane, et les angles de ces villes vers les rayons du soleil il mesura avec une erreur. Et pourtant, il a réussi à obtenir un résultat très proche des données modernes (6 371 km). Certes, selon les étapes qu'il a envisagées, si grecque, alors oui, sa réponse est de 6916 km, et si les étapes des pharaons égyptiens (c'était en Egypte et la distance pouvait y être indiquée), alors sa réponse est 8397 km est bien plus réel.
Cependant, Posidonius était encore plus confus. Mais il ne comptait pas par l'ombre du soleil, mais par l'emplacement de l'étoile Canopus dans le ciel d'Alexandrie et de l'île grecque de Rhodes, qui étaient séparés par les mêmes 5000 stades. Mais ces points ne se trouvaient pas non plus sur le même méridien, et les Grecs mesuraient les distances maritimes avec beaucoup moins de précision. En conséquence, selon ses calculs, la Terre s'est avérée être presque un tiers de moins que celle d'Eratosthène.
Oui, les Grecs se sont trompés dans leurs calculs, mais la principale chose qu'ils ont faite a été de trouver une méthode pour mesurer la taille de la Terre sans quitter sa surface. Ensuite, il s'agissait d'améliorer les données géographiques et les instruments de mesure. Eh bien, les Grecs ne se sont pas arrêtés et ont compris comment calculer la distance à la Lune et au Soleil.