Vous êtes-vous déjà demandé à quoi ressemblerait la vie si la Terre n'était pas une sphère, mais avait une forme différente? Nous tenons pour acquis le bon fonctionnement de notre planète à travers le système solaire et les couchers de soleil lents dont nous pouvons profiter grâce à la symétrie de rotation de la Terre. De plus, la Terre sphérique vous permet de déterminer le moyen le plus rapide pour vous rendre du point A au point B: il suffit de marcher dans un cercle qui passe par ces deux points et coupe la sphère en deux. Nous utilisons ces chemins les plus courts, appelés chemins géodésiques, pour planifier les routes des avions et calculer les orbites des satellites.

Mais que se passerait-il si nous vivions à Cuba? Notre monde basculerait davantage, les horizons sont courbes et le chemin le plus court entre le point A et le point B est plus difficile à trouver. Vous ne passerez peut-être pas beaucoup de temps à imaginer votre vie sur un cube, mais les mathématiciens le feront: ils étudient à quoi ressembleraient nos voyages sur une variété de formes. Et la solution récente à l' une des questions fondamentales sur le dodécaèdre a généralement changé la vision de l'objet qui était sous nos yeux depuis des milliers d'années.
Trouver le chemin le plus court dans les deux sens (d'un point vers le même point autour du cube) pour un corps géométrique donné peut sembler une tâche simple. Après tout, vous reviendrez certainement là où vous avez commencé, non?
En fait, cela dépend de la forme ou du corps sur lequel vous marchez. Si c'est une sphère, alors oui. (Et oui, nous omettons le fait que la Terre n'est pas une sphère idéale, et sa surface n'est pas entièrement lisse.) Sur la sphère, les chemins se répètent le long d'une ligne droite «grands cercles», géodésiques, par exemple, l'équateur. Si vous faites le tour de l'équateur, après environ 25 000 miles, vous effectuerez un cercle complet et reviendrez là où vous avez commencé.
Dans un monde cubique, les lignes géodésiques ne sont pas si évidentes. Trouver un chemin droit sur une face est facile car chaque face est plate. Mais si vous vous promeniez dans le monde cubique, comment continueriez-vous à marcher droit lorsque vous atteigniez le bord?
Il y a un vieux problème mathématique amusant qui illustre la réponse à notre question. Imaginez une fourmi dans un coin d'un cube qui veut se rendre dans le coin opposé. Quel est le chemin le plus court sur la surface d'un cube du point A au point B?
Imaginez les nombreux chemins qu'une fourmi pourrait emprunter.

Mais lequel est le plus court? Il existe une manière ingénieuse de résoudre le problème. Aplatissons le cube!
Si le cube était en papier, vous pouvez le couper le long des bords et aplatir la feuille pour obtenir ce motif déplié.

Dans un monde aussi plat, il est facile de trouver le chemin le plus court de A à B: tracez simplement une ligne droite entre eux.

Pour voir ce que sera la ligne géodésique dans le monde du cube, replacez simplement le cube. Voici notre raccourci.

«Aligner» le cube fonctionne parce que chaque face du cube est plate, donc rien n'est déformé lorsque nous déplions le corps le long des bords. (Cette tentative de "déplier" la sphère ne fonctionnera pas, car nous ne pouvons pas aplatir la sphère sans la déformer.)
Maintenant que nous avons une idée de ce à quoi ressemblent les chemins en ligne droite sur un cube, revenons à la question de savoir si nous pouvons suivre un chemin droit et revenir là où nous avons commencé. Contrairement à une sphère, sur un cube, tous les chemins rectilignes ne nous ramènent pas au début.
Mais de tels itinéraires aller-retour sont possibles. Avec une astuce! Veuillez noter que la fourmi peut continuer le chemin que nous avons indiqué ci-dessus et revenir là où elle a commencé. Sur un cube, un cercle complet crée un chemin qui ressemble plus à un diamant.

En suivant ce chemin (aller et retour), la fourmi doit passer par un autre sommet (point B) avant de revenir à son point de départ. C'est le hic: chaque chemin droit qui commence et se termine au même sommet doit passer par un autre sommet du cube.
Il s'avère que cela est vrai pour quatre des cinq solides platoniciens. Dans un cube, un tétraèdre, un octaèdre et un icosaèdre, tout chemin droit qui commence et se termine au même sommet doit passer par un autre sommet le long du chemin. Les mathématiciens l'ont prouvé il y a cinq ans, mais le dodécaèdre ne figurait pas sur leur liste. Nous y reviendrons un peu plus tard.

Pour comprendre pourquoi ce fait sur les géodésiques est vrai pour quatre des cinq solides platoniques, nous utiliserons la méthode du tumbling et passerons au monde tétraédrique, où cette méthode peut être mieux démontrée.
Imaginez commencer par le haut du tétraèdre et marcher en ligne droite le long du bord. Placez le tétraèdre de sorte que le chemin commence à partir du bord inférieur.
Lorsque nous rencontrons une arête, nous retournons le tétraèdre pour que notre chemin continue le long de la face qui s'avère être en dessous:

De telles rotations permettent de suivre notre chemin de la même manière que nous le ferions en dépliant un cube:

La trajectoire de les rotations ci-dessus représentent ce chemin à la surface du tétraèdre:

Les cinq tours du tétraèdre correspondent aux cinq faces supplémentaires traversées par notre route.
Nous pouvons maintenant imaginer n'importe quel chemin à la surface du tétraèdre comme un chemin dans cet espace "tournant". Définissons notre point de départ A et voyons où il se termine après quelques tours.
Lorsque notre chemin quitte le point A, le tétraèdre tombe du côté opposé. Cela soulève le point A du sol.

Le Vertex A monte temporairement dans notre monde en rotation. Nous ne spécifions généralement pas l'emplacement du point A lors de la création de notre espace de rotation, mais voici où il pourrait apparaître si nous regardions vers le bas.

Alors que notre chemin continue, le tétraèdre retombe. Il peut le faire dans l'une des deux directions possibles, mais dans tous les cas, A est à nouveau en bas.
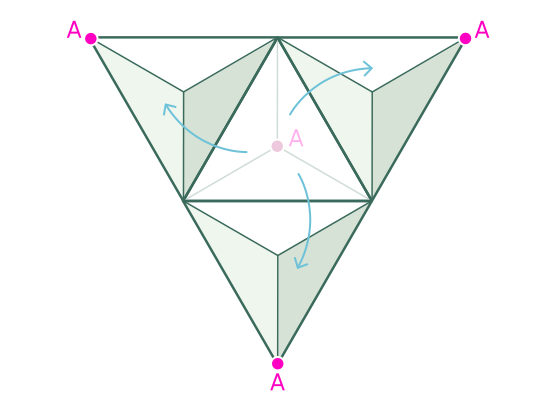
Quand on fait tomber le tétraèdre dans toutes les directions possibles, on obtient un saut périlleux qui ressemble à ceci:

Il s'avère une sorte de treillis dû au fait que les faces triangulaires équilatérales du tétraèdre coïncident les unes avec les autres.

Cette grille triangulaire nous dit deux choses intéressantes sur notre monde en rotation. Premièrement, tous les points auxquels les sommets du tétraèdre peuvent atterrir sont des "points de réseau" (représentés sur le diagramme) ou des points avec des coordonnées entières. C'est parce qu'une unité dans notre système de coordonnées est égale à la longueur d'un bord du tétraèdre.
Deuxièmement, regardez où pourrait finir A. Les
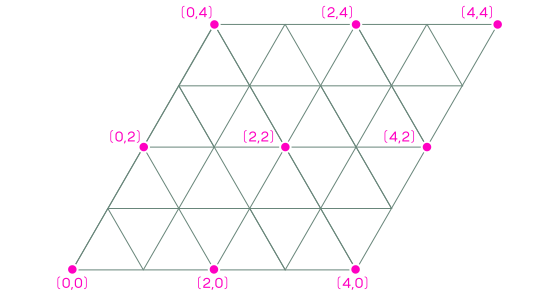
coordonnées de A sont toujours paires. Chaque fois que A est en panne, il y revient après deux tours, de sorte que tous les points d'atterrissage possibles pour A sont placés à des intervalles de deux longueurs de côtes dans chaque direction de rotation.
Voyons maintenant ce que cela dit sur les lignes géodésiques. Rappelez-vous qu'un chemin dans un tétraèdre qui commence et se termine au point A sera un segment de ligne droite dans l'espace de rotation, commençant au point A (0,0) et se terminant à un autre point A. Et lorsque les points de début et de fin du chemin coïncider à un seul A, que sera-t-il au milieu du chemin?
Même dans notre système de coordonnées déroutant, la formule standard pour calculer le milieu d'un segment de ligne fonctionne toujours, nous pouvons donc trouver ses coordonnées en fonction des coordonnées des points d'extrémité.
Puisque les deux coordonnées du point de départ sont 0 et que les deux coordonnées du point final sont paires, les coordonnées du milieu sont des entiers. Autrement dit, le milieu sera l'un des points du réseau et, comme nous l'avons noté ci-dessus, cela signifie qu'il correspond au sommet du triangle dans l'espace de rotation.
Par exemple, le chemin de (0,0) à (4,2) a un point médian (2,1), c'est le point de treillis marqué dans notre grille.

Il s'avère qu'à la surface du tétraèdre, le chemin de A et de retour doit passer par un autre sommet.
Puisque chaque «atterrissage» possible pour A a des coordonnées paires, le point médian de chaque chemin géodésique commençant et se terminant en A correspondra à un point de grille. Cela prouve que chaque ligne géodésique de A à A à la surface du tétraèdre doit passer par un autre sommet.
Ce raisonnement simple a été élaboré en 2015 par les mathématiciens Diana Davis, Victor Dods, Cynthia Traub et Jed Young.
Ils ont utilisé une méthode similaire mais beaucoup plus complexe pour prouver la même chose pour un cube. L'année suivante, Dmitry Fuks a confirmérésultats pour l'octaèdre et l'icosaèdre. Pour cette raison, nous savons que pour un tétraèdre, un cube, un octaèdre et un icosaèdre, il n'y a pas de chemins rectilignes allant d'un sommet à lui-même qui ne passeraient pas par un autre sommet.
Mais la question de l'existence de tels chemins à la surface du dodécaèdre est restée ouverte jusqu'en 2019, lorsque les mathématiciens Jayadev Atreya, David Avlikino et Patrick Hooper ont prouvé que c'était bien possible. En fait, ils ont trouvé une infinité de chemins rectilignes à la surface du dodécaèdre qui commencent et se terminent au même sommet sans passer par d'autres.
En voici un, représenté sur un scan du dodécaèdre, se cachant à la vue de tous.

Les solides platoniques ont été étudiés ensemble pendant des milliers d'années parce qu'ils ont tant de points communs. Mais maintenant, nous savons quelque chose de nouveau sur le dodécaèdre, et cela le distingue clairement des autres corps.
Cette découverte mystérieuse montre que peu importe notre compréhension des objets mathématiques, il y a toujours quelque chose à apprendre. Il est important de se rappeler que le chemin du problème à la solution ne sera pas toujours simple!
Tâches
1. Si la longueur d'arête d'un cube est 1, quel est le chemin le plus court pour une fourmi d'un sommet à l'autre?
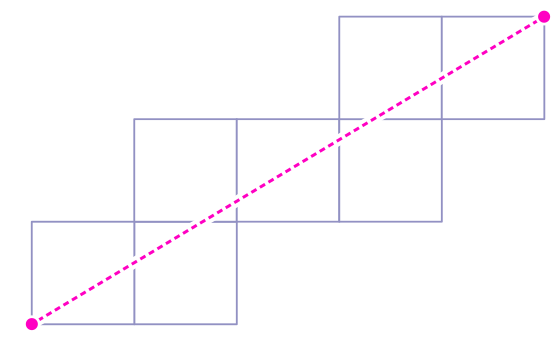
2. Expliquez pourquoi le diagramme ci-dessous ne peut pas être un chemin de rotation sur un cube.

3. L'une des difficultés de la "rotation" d'un cube est que le point A n'a pas de position finale unique associée à la position finale du cube. Par exemple, même si le cube est au même endroit, tournant le long d'un chemin rouge ou bleu, le point A est dans des positions différentes. Déterminez où A sera après les virages le long de la trajectoire rouge et bleue.

4. C'est la trajectoire des rotations du cube.
Tracez un chemin sur la surface du cube, en commençant au point A.

Réponses
Cliquez pour voir la réponse 1
— 1 2.

, AB √5.

, AB √5.
Cliquez pour voir la réponse 2
, 1 . , , .

, «» , .

, «» , .
, 3
.
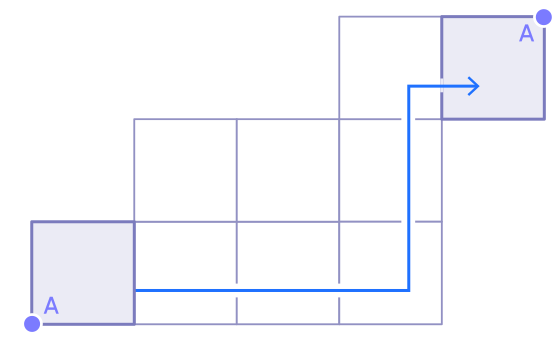

, .


, .
, 4

