Très probablement, chacun de vous a entendu le terme «transformations affines» au moins une fois dans sa vie. En effet, tout le monde en parle constamment: «invariance aux transformations affines», «augmentation par transformations affines», «transformations affines en infographie», etc. Cependant, tout le monde ne peut pas répondre immédiatement à une question simple: «Dites-nous ce que sont les transformations affines en termes simples».
Vous pouvez? Quoi qu'il en soit, discutons un peu de cette question.
Qu'est-ce que la transformation affine?
Commençons par les classiques - définition de Wikipedia.
La transformation affine (du latin affinis "toucher, fermer, adjacent") est une cartographie d'un plan ou d'un espace en lui-même, dans laquelle des lignes parallèles passent en lignes parallèles, des lignes qui se croisent en des lignes qui se croisent, des lignes qui se croisent en des lignes qui se croisent.
Clarifions un peu.
Premièrement, que signifie «auto-cartographie» ? Cela signifie que si nous étions dans l'espace , alors après l'éducation, nous devons y rester. Par exemple , si nous avons appliqué une sorte de transformation à un rectangle et avons obtenu un parallélépipède, puis nous sommes partis
en
. Mais si nous obtenons un autre rectangle du rectangle, alors tout va bien, nous avons mappé l'espace d'origine sur nous-mêmes. Formellement, il est décrit comme suit: "transformation
mappe l'espace
à
". S'il est écrit à l'aide de formules
.
-, « »? , , . , . , . , . - .
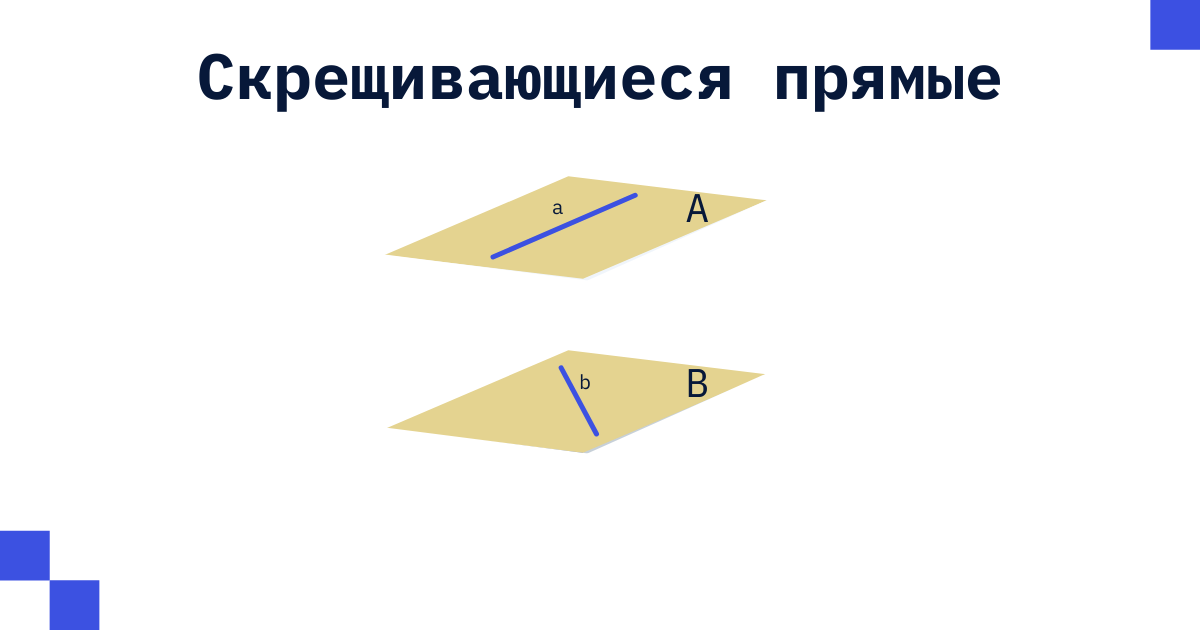
, - . , : . , 2 . , . , - , .
, - .
( ).
, , .
, , , , .
, « ». .. - , - .
- , - . : - . , ( , ).
, . , .
. -
.
:
, :
: , , ..
.
-
,
- ,
.
, ,
- .
, . .
- ? .
.
, :
:
? , - . .. . .

-
:
:
, , , 1 , 1. .
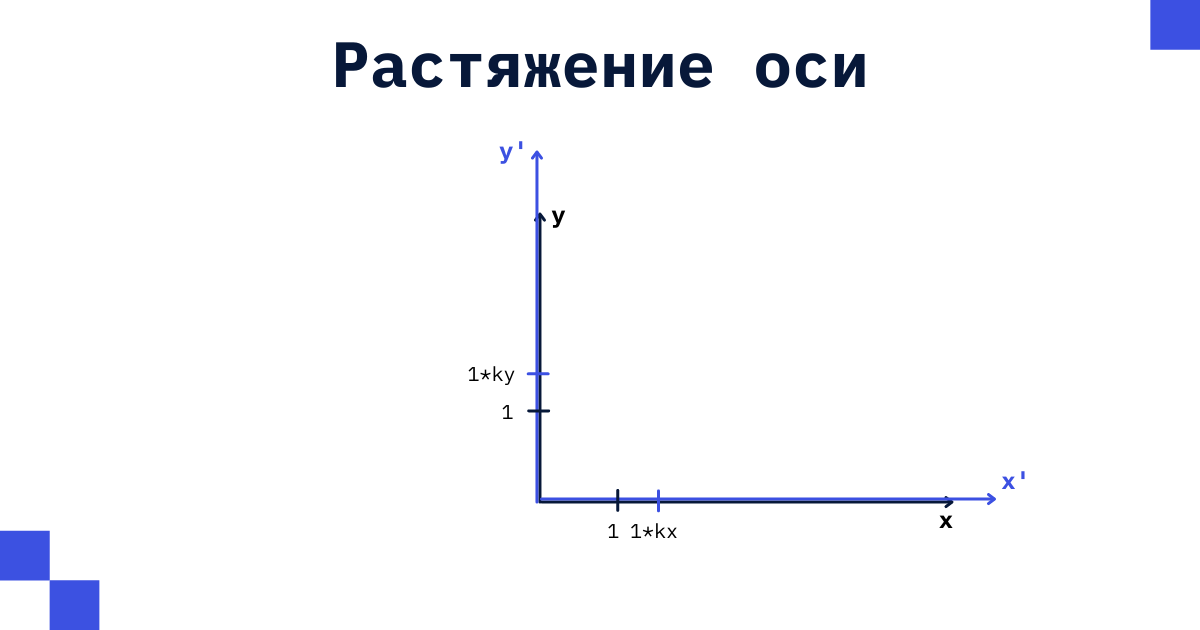
, -1,
1. ? ,
.
.
(..
).
,
.
, :
, . , , .

Ce court article vous permettra de ressentir un peu plus fortement les «intérieurs» des transformations affines (nous l'espérons). Après l'avoir lu, essayez de répondre à la question que nous nous sommes posée au tout début - «Dites-nous ce que sont les transformations affines en termes simples». Pouvez-vous maintenant?
PS Au fait, ce serait bien de ne pas nous croire sur parole et de le vérifier nous-mêmes - et les matrices que nous avons utilisées sont définitivement non dégénérées? Peut-être avons-nous fait quelque chose d'illégal? ...