
Aujourd'hui, la NASA a tweeté un message sur le début du mouvement du rover Perseverance à travers la planète rouge. Le rover a parcouru quelques mètres pour vérifier le châssis. Tout s'est bien terminé, les systèmes fonctionnent comme il se doit. De plus, le rover a photographié ses propres traces. L'heure totale d'arrivée est de 33 minutes, période pendant laquelle le rover a parcouru 6,5 mètres.
Pour autant que vous puissiez en juger, le rover se porte bien. Mais, si vous vous en souvenez, le rover a atterri à la surface à l'aide de la Sky Crane. Le système, qui permettait un atterrissage en douceur à l'aide des câbles, s'est séparé à un moment donné du rover et s'est envolé, utilisant les réserves de carburant restantes. Mais où est-elle allée exactement et jusqu'où pourrait-elle aller? Let le comte toi même.
La NASA a déjà téléchargé une photo de la plate-forme tombée à la surface de Mars. L'agence connaît son emplacement exact. Mais c'est cool de calculer la distance parcourue par la plate-forme, en ayant à sa disposition les données d'atterrissage initiales et la vidéo envoyée par le rover.
Pour les calculs, nous utiliserons la taille angulaire de la plate-forme d'atterrissage.
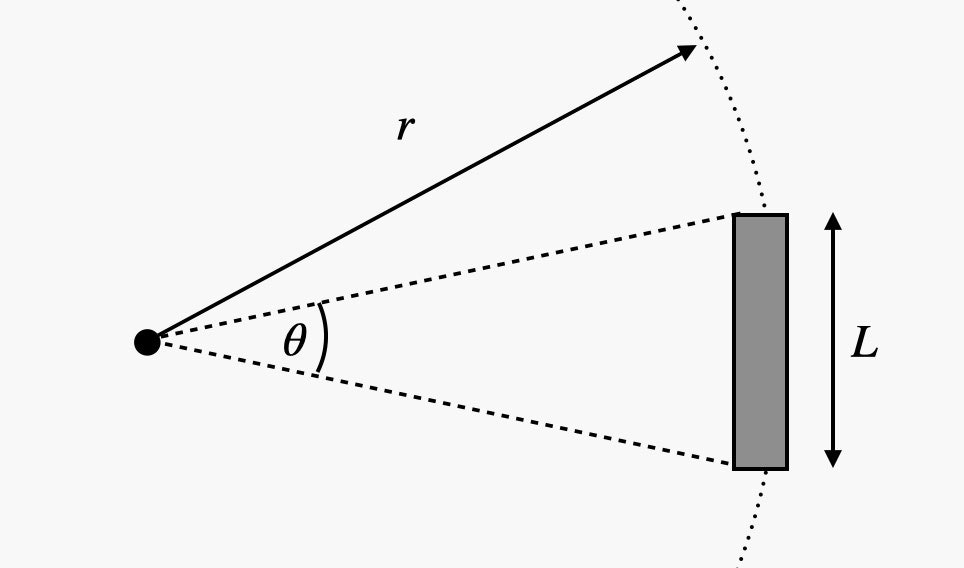
Sur Habré, cela n'a guère de sens de parler de la taille angulaire, alors passons aux calculs tout de suite.
Le calcul de la taille angulaire est très simple, voici la formule.
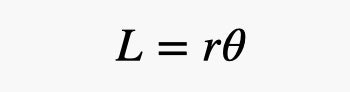
Pourquoi avons-nous besoin d'une taille angulaire? Eh bien, si nous le savons, en plus nous connaissons la taille réelle, nous pouvons facilement déterminer la distance à l'objet - ce sera r. L'option de calcul idéale est d'utiliser juste une cheville plate, il est plus facile d'effectuer des calculs avec elle. Mais comme nous n'avons pas de piquet, mais une plate-forme, ce sera un peu plus difficile. Mais encore, il ne devrait y avoir aucun problème lors des calculs.
La première chose que je dois faire est de déterminer le champ de vision de la caméra du rover orientée vers le haut.Il n'y a pas de caractéristiques exactes, alors estimons approximativement. Voici une plate-forme avec le rover suspendu à un câble avant l'atterrissage.

Selon la NASA, le câble mesure 6,4 mètres de long - nous connaissons donc le ® sur cette photo. De plus, nous pouvons déterminer la longueur de l'embarcadère. Si nous prenons sa largeur, elle est de 2,69 mètres, alors la taille angulaire réelle, vue du rover, est de 0,42 radians. Utilisons ce nombre pour définir la largeur de l'image vidéo entière avec un champ de vision angulaire (FOV) de 0,627 radians (soit 35,9 degrés).
Tout cela est extrêmement important pour les calculs ultérieurs. Avec ces données, vous pouvez mesurer la taille angulaire de la plate-forme d'atterrissage et calculer la distance au mobile. Pour ce faire, vous pouvez utiliser un outil spécial, Tracker Video Analysis. Il permet d'analyser la taille des objets de la vidéo. Nous construisons un tel calendrier.
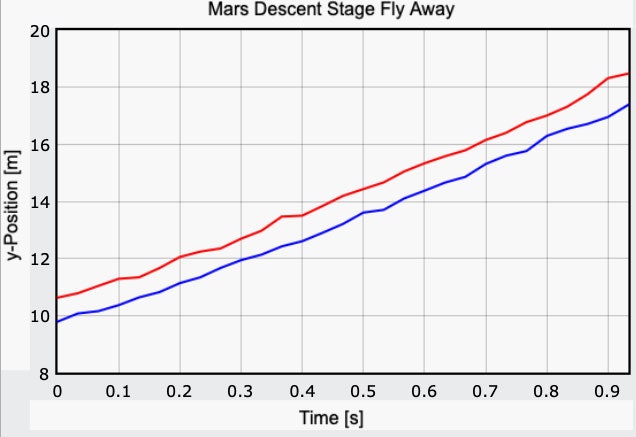
On pourrait penser que le graphique serait parabolique, ce qui montrerait une accélération constante de la plate-forme. Mais il semble que rien de tel ne se soit produit - si la plate-forme accélérait, alors c'était minime. Nous calculons la vitesse - et nous obtenons environ 8,2 m / s.
Arrêter! Après tout, nous avons autre chose. Le fait est que la plate-forme d'atterrissage part en biais, comme cela a été dit plus d'une fois. Et cela a du sens - si la plate-forme volait simplement vers le haut, alors après avoir utilisé tout le carburant, toute cette structure s'effondrerait alors vers le bas - directement sur le rover. La vidéo permet de déterminer l'angle d'inclinaison. Voici un graphique et une formule qui aident.
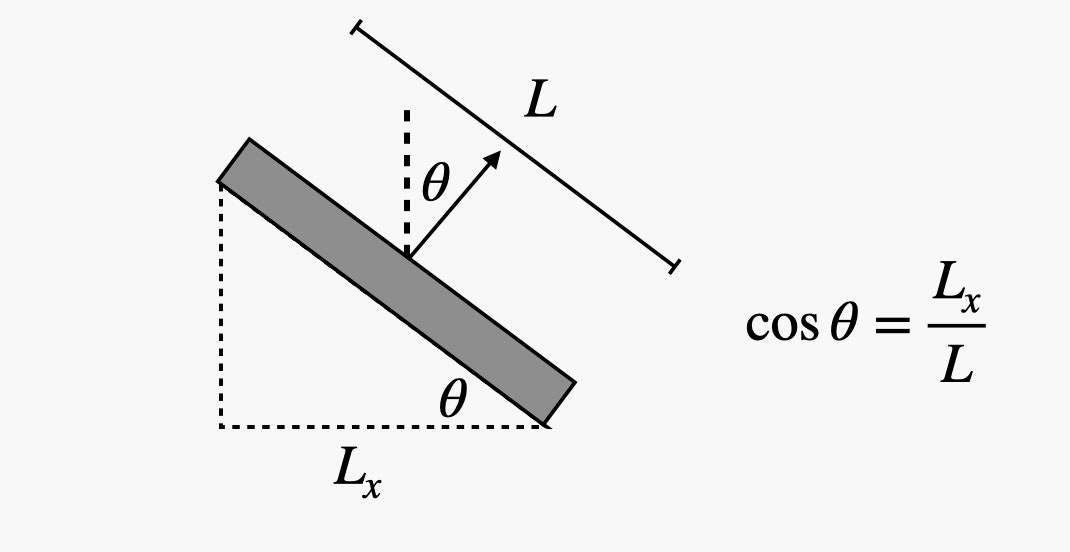
En utilisant la distance connue aux moteurs, ainsi que la distance apparente, nous obtenons un angle d'inclinaison de 52 degrés par rapport à la verticale. Espérons que tout est correct, car cet indicateur est nécessaire pour d'autres calculs.
Mouvement de la plate-forme
Nous sommes maintenant prêts à nous attaquer à un problème physique important. Cela ressemble à ça.
L'atterrisseur sur Mars effectue une manœuvre de départ pour se rendre à une distance de sécurité du rover Perseverance. Le module démarre les propulseurs pour atteindre une vitesse de 8,2 m / s à un angle de lancement de 52 degrés par rapport à la verticale. Si Mars a un champ gravitationnel de 3,7 N / kg, à quelle distance du rover tombera-t-il? Vous pouvez supposer que la résistance de l'air est négligeable.
Il y a une formulation du problème. Maintenant, nous avons besoin d'une réponse. Le point clé ici est que le mouvement dans la direction horizontale (appelons-le la direction x) se fait à une vitesse constante. Quant à la vitesse de descente (direction y), nous avons ici une accélération - g (où g = 3,7 N / kg), causée par la force de gravité. Comme il est constant et n'agit que verticalement, nous pouvons diviser la tâche en deux - en fait, le mouvement dans le plan horizontal et le mouvement dans le plan vertical. Ces deux éléments d'une même tâche sont indépendants, ils ne sont liés que par le temps.
Commençons par nous déplacer verticalement.

Pour effectuer les calculs requis, nous utilisons le cosinus. L'équation suivante pour le mouvement à accélération constante nous aidera.

Les positions de début et de fin sont nulles (c'est la surface). Voici une expression pour aider à déterminer l'heure.

Si nous utilisons y0 avec une distance de 6,4 m (ce qui est réaliste), nous devons utiliser l'équation quadratique. Ce n'est pas si difficile. Mais on peut aussi utiliser le temps dans le mouvement horizontal du véhicule de descente. Voici l'équation du mouvement horizontal.
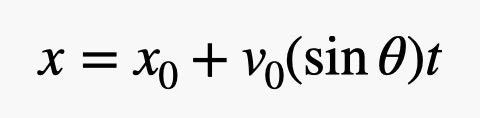
La vitesse dépend du sinus de l'angle. Maintenant, vous pouvez simplement laisser x0 à zéro et remplacer time par l'expression ci-dessus. En conséquence, nous obtenons ceci.
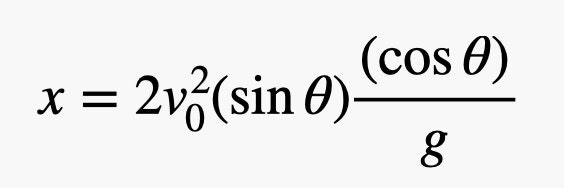
En substituant nos valeurs, nous constatons que la distance que la plate-forme s'est éloignée est de 17,6 mètres. Mais non, ce n'est pas du tout le cas. Nous le savons grâce aux photos publiées par la NASA. Selon les images, la plate-forme a atterri à une distance d'environ un kilomètre du rover. Nous changeons l'état du problème.
Afin de ne pas présenter de danger pour le rover, la plate-forme doit s'envoler à une distance d'environ 1 km. Vitesse de descente - 8,2 m / s avec un angle d'inclinaison d'environ 52 degrés. Quelle sera la hauteur de la plate-forme avant l'arrêt des moteurs? Nous utilisons cette formule.

Nous utilisons maintenant le temps pour résoudre l'équation suivante.

Si nous effectuons des calculs, il s'avère que l'indicateur de départ vertical est de 43 km. Pourquoi donc? Le fait est que la plate-forme a accéléré lorsque les moteurs ont été lancés.
Essayons de faire quelques calculs en Python. Le calcul se compose de deux parties. Premièrement, pendant un certain temps, la fusée volera à une accélération constante de 52 degrés. Il suffit de sélectionner le temps et l'accélération, puis de calculer la chute du corps à la surface de Mars. Voici le code du programme qui effectue tous les calculs.
GlowScript 3.0 VPython
v0=8.2
g=3.7
theta=52*pi/180
x=1000
y0=.5*g*(x/(v0*sin(theta)))**2-x*cos(theta)/sin(theta)
tgraph=graph(width=550, height=350, xtitle="x-position [m]", ytitle="yx-Position [m]", title="Trajectory of Descent Stage Fly Away")
f1=gcurve(color=color.blue)
#starting position
x=0
y=6.4
#rocket firing time
tf=7
#rocket acceleration
a=6
#initial velocity
vy=v0*cos(theta)
vx=v0*sin(theta)
#time
t=0
dt=0.01
#rockets firing
while t<tf:
vy=vy+a*cos(theta)*dt
vx=vx+a*sin(theta)*dt
y=y+vy*dt
x=x+vx*dt
t=t+dt
f1.plot(x,y)
#to record max height
ymax=0
#projectile motion
while y>=0:
vy=vy-g*dt
y=y+vy*dt
x=x+vx*dt
if vy<0.1:
ymax=y
t=t+dt
f1.plot(x,y)
print("Descent Range = ",x," m")
print("Maximum Altitude = ",ymax," m")
print("Fly Away Time = ",t, " seconds")
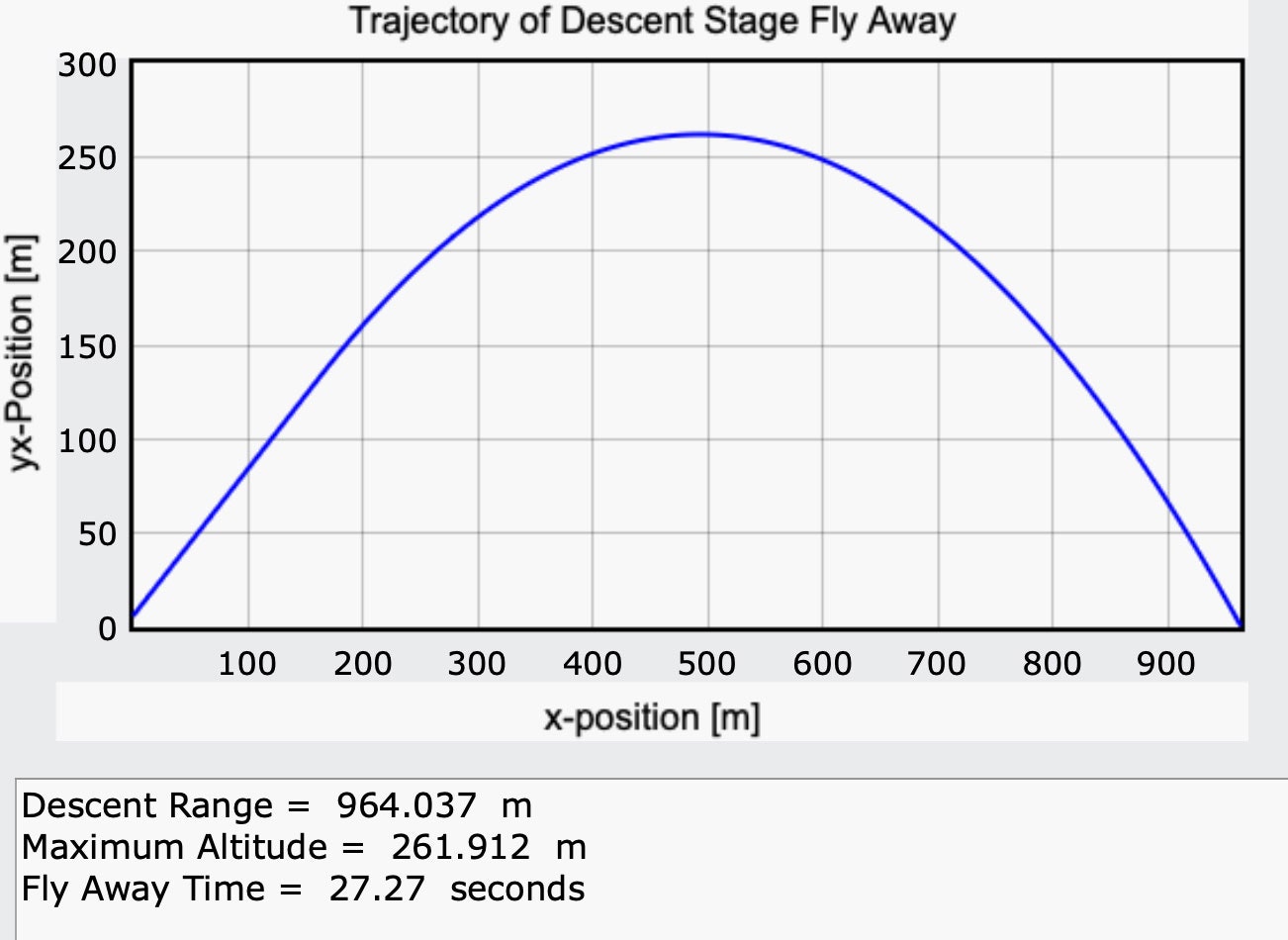
Pour les calculs, nous prenons l'accélération de la plate-forme de 6 m / s 2 et le temps de fonctionnement des moteurs en 7 secondes. Et nous obtenons déjà une valeur normale de 964 mètres, ce qui est déjà très similaire à la vérité. Pour terminer.
