
Dans cet article, nous allons jeter un coup d'œil sous le capot des algorithmes d'infographie, parcourir les principes de base du lancer de rayons étape par étape et écrire une implémentation simple en Python. Pas de bibliothèques graphiques tierces - juste NumPy et du code nu dans le compilateur.
: / , , .
:
A B — : 1, 2, 3,…, n, — , A B, B — A ();
— — , . v ||v||;
— 1: ||v|| = 1;
, , 1, — : u = v/||v||;
: <v, v> = ||v||².
— , . .
, :
( );
( . 1, );
( , );
;
, ( ).

— (, 3x2). 3 2 - . , (), . . , 3x2 300x200 .
:
p(x, y, z) :
p
(), p, , :
, :
p
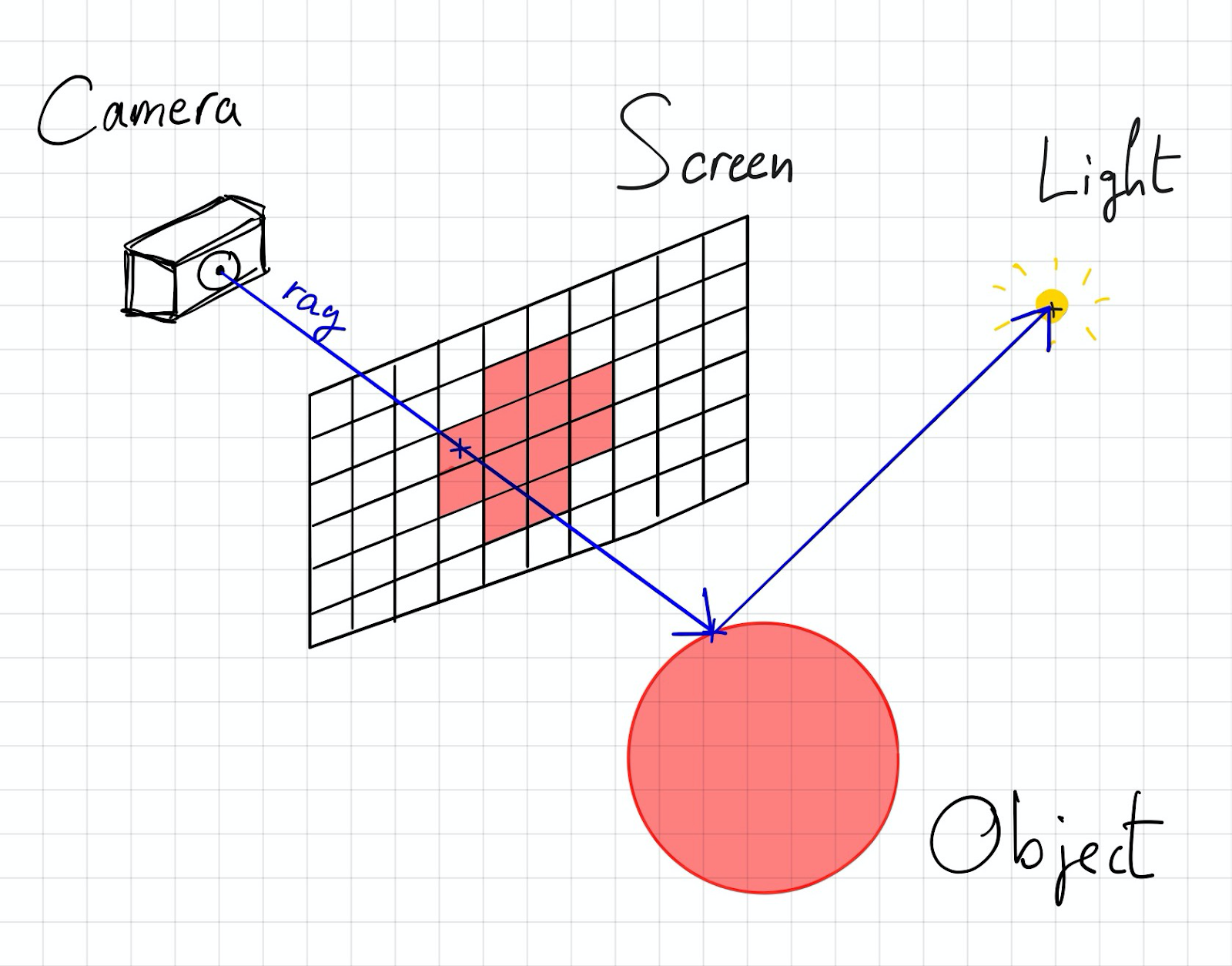
, . , . , , , , ( ).
, , . , . , .

, (x = 0, y = 0, z = 1), , x y. .
import numpy as np
import matplotlib.pyplot as plt
width = 300
height = 200
camera = np.array([0, 0, 1])
ratio = float(width) / height
screen = (-1, 1 / ratio, 1, -1 / ratio) # , , ,
image = np.zeros((height, width, 3))
for i, y in enumerate(np.linspace(screen[1], screen[3], height)):
for j, x in enumerate(np.linspace(screen[0], screen[2], width)):
# image[i, j] = ...
print("progress: %d/%d" % (i + 1, height))
plt.imsave('image.png', image)
— , ;
, ( ): , , , . -1 1 x -1/ratio 1/ratio y, ratio — , . , , , . ( ): 2 /(2/ratio) = ratio, 300x200;
x y, ;
— — .
: (), p, , ...
. , () p?
«», «». , : , , .
, , , . :

, — 3D-. t = 0 , t . , t.
, , (O) (D) :
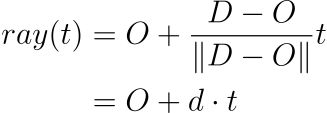
d .
:
import numpy as np
import matplotlib.pyplot as plt
def normalize(vector):
return vector / np.linalg.norm(vector)
width = 300
height = 200
camera = np.array([0, 0, 1])
ratio = float(width) / height
screen = (-1, 1 / ratio, 1, -1 / ratio) # , , ,
image = np.zeros((height, width, 3))
for i, y in enumerate(np.linspace(screen[1], screen[3], height)):
for j, x in enumerate(np.linspace(screen[0], screen[2], width)):
pixel = np.array([x, y, 0])
origin = camera
direction = normalize(pixel - origin)
# image[i, j] = ...
print("progress: %d/%d" % (i + 1, height))
plt.imsave('image.png', image)
normalize(vector), ... , ;
, . , z = 0, , , x y;
, . .
— . , r () ().
, C r X , :
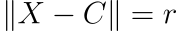
, , X — C:

:
objects = [
{ 'center': np.array([-0.2, 0, -1]), 'radius': 0.7 },
{ 'center': np.array([0.1, -0.3, 0]), 'radius': 0.1 },
{ 'center': np.array([-0.3, 0, 0]), 'radius': 0.15 }
]
.
, , . , , t. , : t ray(t) ?

, t. , t², t¹, t⁰, a, b c, . :

d , a = 1. :
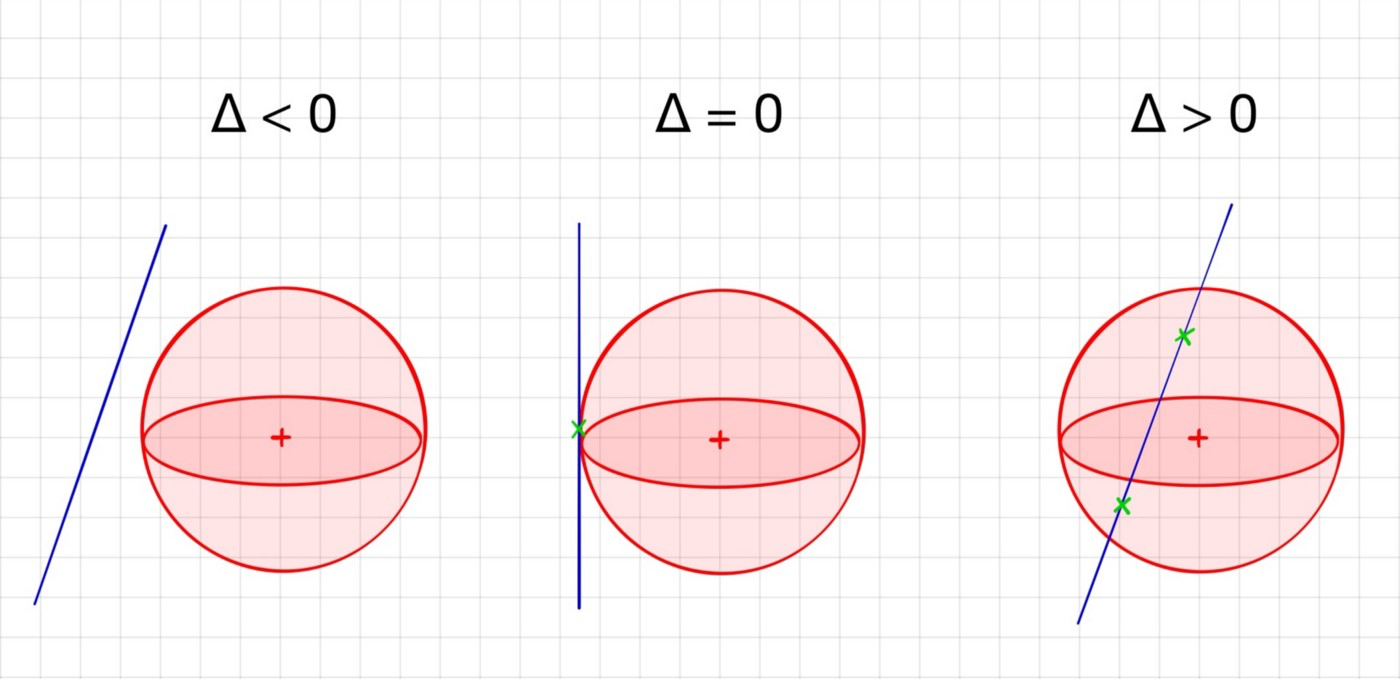
. , . , , None:
def sphere_intersect(center, radius, ray_origin, ray_direction):
b = 2 * np.dot(ray_direction, ray_origin — center)
c = np.linalg.norm(ray_origin — center) ** 2 — radius ** 2
delta = b ** 2 — 4 * c
if delta > 0:
t1 = (-b + np.sqrt(delta)) / 2
t2 = (-b — np.sqrt(delta)) / 2
if t1 > 0 and t2 > 0:
return min(t1, t2)
return None
, , t1 t2 . , , , , d , -d (, ).
: (), p, , [...]. .
, sphere_intersect() , , . , :
def nearest_intersected_object(objects, ray_origin, ray_direction):
distances = [sphere_intersect(obj['center'], obj['radius'], ray_origin, ray_direction) for obj in objects]
nearest_object = None
min_distance = np.inf
for index, distance in enumerate(distances):
if distance and distance < min_distance:
min_distance = distance
nearest_object = objects[index]
return nearest_object, min_distance
, nearest_object = None, , , min_distance — .
, :
nearest_object, distance = nearest_intersected_object(objects, o, d)
if nearest_object:
intersection_point = o + d * distance
:
import numpy as np
import matplotlib.pyplot as plt
def normalize(vector):
return vector / np.linalg.norm(vector)
def sphere_intersect(center, radius, ray_origin, ray_direction):
b = 2 * np.dot(ray_direction, ray_origin — center)
c = np.linalg.norm(ray_origin — center) ** 2 — radius ** 2
delta = b ** 2 — 4 * c
if delta > 0:
t1 = (-b + np.sqrt(delta)) / 2
t2 = (-b — np.sqrt(delta)) / 2
if t1 > 0 and t2 > 0:
return min(t1, t2)
return None
def nearest_intersected_object(objects, ray_origin, ray_direction):
distances = [sphere_intersect(obj['center'], obj['radius'], ray_origin, ray_direction) for obj in objects]
nearest_object = None
min_distance = np.inf
for index, distance in enumerate(distances):
if distance and distance < min_distance:
min_distance = distance
nearest_object = objects[index]
return nearest_object, min_distance
width = 300
height = 200
camera = np.array([0, 0, 1])
ratio = float(width) / height
screen = (-1, 1 / ratio, 1, -1 / ratio) # , , ,
objects = [
{ 'center': np.array([-0.2, 0, -1]), 'radius': 0.7 },
{ 'center': np.array([0.1, -0.3, 0]), 'radius': 0.1 },
{ 'center': np.array([-0.3, 0, 0]), 'radius': 0.15 }
]
image = np.zeros((height, width, 3))
for i, y in enumerate(np.linspace(screen[1], screen[3], height)):
for j, x in enumerate(np.linspace(screen[0], screen[2], width)):
pixel = np.array([x, y, 0])
origin = camera
direction = normalize(pixel — origin)
#
nearest_object, min_distance = nearest_intersected_object(objects, origin, direction)
if nearest_object is None:
continue
#
intersection = origin + min_distance * direction
# image[i, j] = ...
print("%d/%d" % (i + 1, height))
plt.imsave('image.png', image)
, , , , , . , . , , , . , — , .
, : near_intersected_object(). , , , , . , : . -, . :
light = { 'position': np.array([5, 5, 5]) }
, , , , , , , ( , ).
# ...
intersection = origin + min_distance * direction
intersection_to_light = normalize(light['position'] — intersection)
_, min_distance = nearest_intersected_object(objects, intersection, intersection_to_light)
intersection_to_light_distance = np.linalg.norm(light['position'] — intersection)
is_shadowed = min_distance < intersection_to_light_distance
, . . , , , . — , . .

, .
, :
# ...
intersection = origin + min_distance * direction
normal_to_surface = normalize(intersection — nearest_object['center'])
shifted_point = intersection + 1e-5 * normal_to_surface
intersection_to_light = normalize(light['position'] — shifted_point)
_, min_distance = nearest_intersected_object(objects, shifted_point, intersection_to_light)
intersection_to_light_distance = np.linalg.norm(light['position'] — intersection)
is_shadowed = min_distance < intersection_to_light_distance
if is_shadowed:
continue
-
, , , — . : ? -.
- — , .
, :
(Ambient color): , ;
(Diffuse color): , , ;
(Specular color): , . ;
(Shininess): , , .
: RGB 0 – 1.

:
objects = [
{ 'center': np.array([-0.2, 0, -1]), 'radius': 0.7, 'ambient': np.array([0.1, 0, 0]), 'diffuse': np.array([0.7, 0, 0]), 'specular': np.array([1, 1, 1]), 'shininess': 100 },
{ 'center': np.array([0.1, -0.3, 0]), 'radius': 0.1, 'ambient': np.array([0.1, 0, 0.1]), 'diffuse': np.array([0.7, 0, 0.7]), 'specular': np.array([1, 1, 1]), 'shininess': 100 },
{ 'center': np.array([-0.3, 0, 0]), 'radius': 0.15, 'ambient': np.array([0, 0.1, 0]), 'diffuse': np.array([0, 0.6, 0]), 'specular': np.array([1, 1, 1]), 'shininess': 100 }
]
, , .
- , : , . :
light = { 'position': np.array([5, 5, 5]), 'ambient': np.array([1, 1, 1]), 'diffuse': np.array([1, 1, 1]), 'specular': np.array([1, 1, 1]) }
, - :
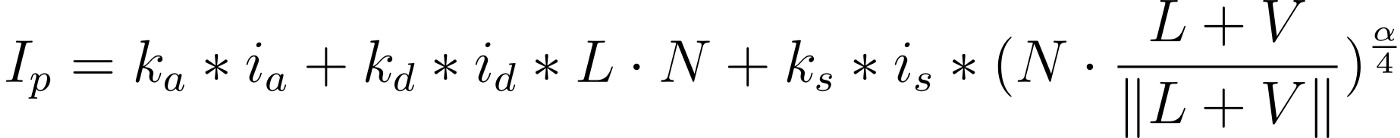
ka, kd, ks — , , ;
ia, id, is — , , ;
L — ;
N — ;
V — ;
α — .
# ...
if is_shadowed:
break
# RGB
illumination = np.zeros((3))
# ambiant
illumination += nearest_object['ambient'] * light['ambient']
# diffuse
illumination += nearest_object['diffuse'] * light['diffuse'] * np.dot(intersection_to_light, normal_to_surface)
# specular
intersection_to_camera = normalize(camera — intersection)
H = normalize(intersection_to_light + intersection_to_camera)
illumination += nearest_object['specular'] * light['specular'] * np.dot(normal_to_surface, H) ** (nearest_object['shininess'] / 4)
image[i, j] = np.clip(illumination, 0, 1)
, 0 1, , .
( ).

, , :
;
.
— , , . , ( ), , .
:
{ 'center': np.array([0, -9000, 0]), 'radius': 9000 — 0.7, 'ambient': np.array([0.1, 0.1, 0.1]), 'diffuse': np.array([0.6, 0.6, 0.6]), 'specular': np.array([1, 1, 1]), 'shininess': 100 }
, , . , , ? .
0 1. 0 , , 1 — . :
{ 'center': np.array([-0.2, 0, -1]), ..., 'reflection': 0.5 }
{ 'center': np.array([0.1, -0.3, 0]), ..., 'reflection': 0.5 }
{ 'center': np.array([-0.3, 0, 0]), ..., 'reflection': 0.5 }
{ 'center': np.array([0, -9000, 0]), ..., 'reflection': 0.5 }
, , , . .
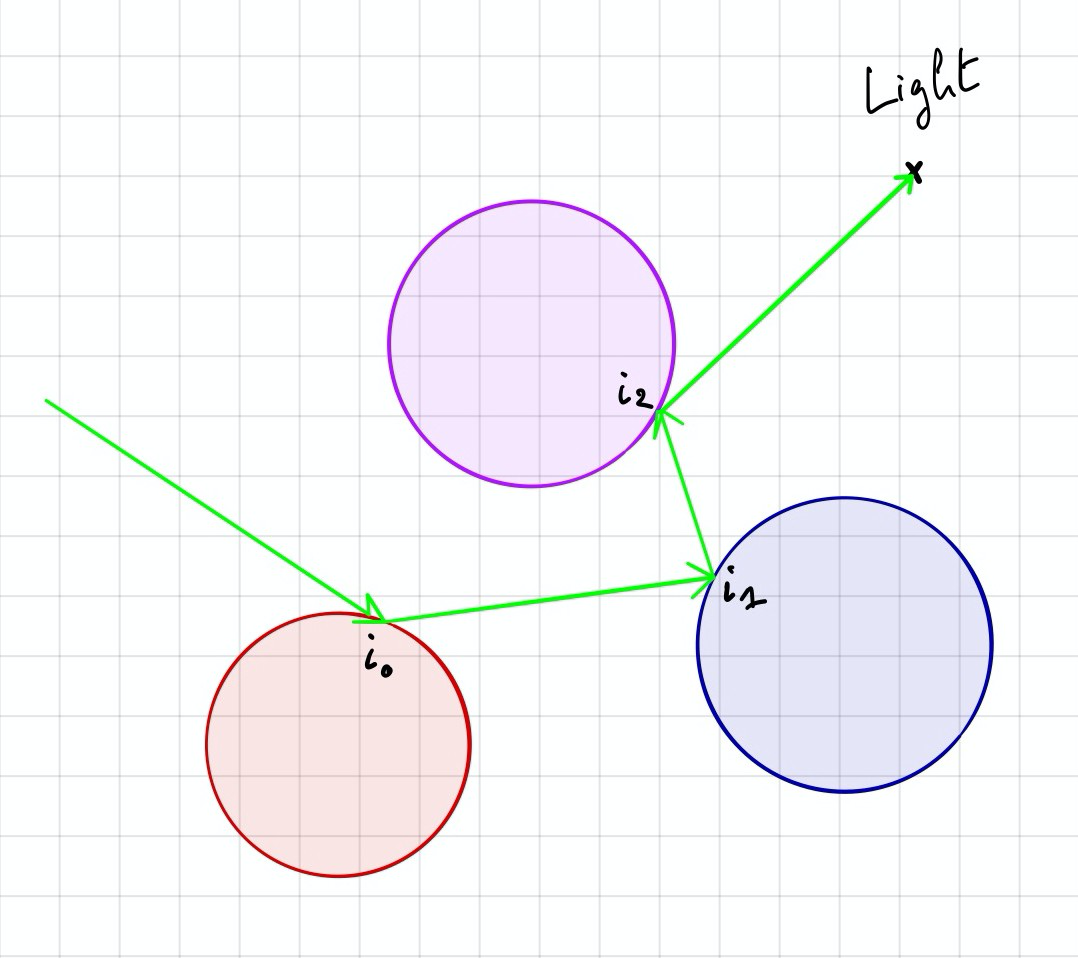
, :

c — ;
i — , - ;
r — .
( , ), .
, . :

R — ;
L — ;
N — .
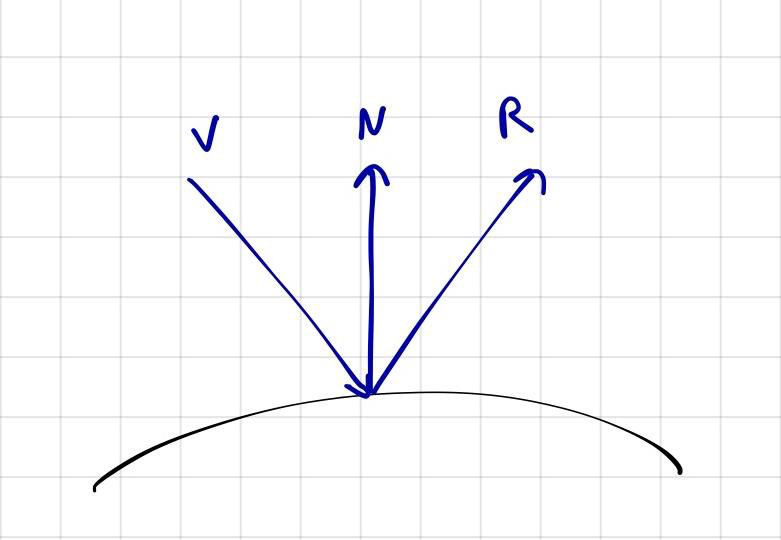
normalize():
def reflected(vector, axis):
return vector — 2 * np.dot(vector, axis) * axis
#
max_depth = 3
#
color = np.zeros((3))
reflection = 1
for k in range(max_depth):
nearest_object, min_distance = # ...
# ...
illumination += # ...
#
color += reflection * illumination
reflection *= nearest_object['reflection']
#
origin = shifted_point
direction = reflected(direction, normal_to_surface)
image[i, j] = np.clip(color, 0, 1)
: , , break .
. :

:
import numpy as np
import matplotlib.pyplot as plt
def normalize(vector):
return vector / np.linalg.norm(vector)
def reflected(vector, axis):
return vector - 2 * np.dot(vector, axis) * axis
def sphere_intersect(center, radius, ray_origin, ray_direction):
b = 2 * np.dot(ray_direction, ray_origin - center)
c = np.linalg.norm(ray_origin - center) ** 2 - radius ** 2
delta = b ** 2 - 4 * c
if delta > 0:
t1 = (-b + np.sqrt(delta)) / 2
t2 = (-b - np.sqrt(delta)) / 2
if t1 > 0 and t2 > 0:
return min(t1, t2)
return None
def nearest_intersected_object(objects, ray_origin, ray_direction):
distances = [sphere_intersect(obj['center'], obj['radius'], ray_origin, ray_direction) for obj in objects]
nearest_object = None
min_distance = np.inf
for index, distance in enumerate(distances):
if distance and distance < min_distance:
min_distance = distance
nearest_object = objects[index]
return nearest_object, min_distance
width = 300
height = 200
max_depth = 3
camera = np.array([0, 0, 1])
ratio = float(width) / height
screen = (-1, 1 / ratio, 1, -1 / ratio) # left, top, right, bottom
light = { 'position': np.array([5, 5, 5]), 'ambient': np.array([1, 1, 1]), 'diffuse': np.array([1, 1, 1]), 'specular': np.array([1, 1, 1]) }
objects = [
{ 'center': np.array([-0.2, 0, -1]), 'radius': 0.7, 'ambient': np.array([0.1, 0, 0]), 'diffuse': np.array([0.7, 0, 0]), 'specular': np.array([1, 1, 1]), 'shininess': 100, 'reflection': 0.5 },
{ 'center': np.array([0.1, -0.3, 0]), 'radius': 0.1, 'ambient': np.array([0.1, 0, 0.1]), 'diffuse': np.array([0.7, 0, 0.7]), 'specular': np.array([1, 1, 1]), 'shininess': 100, 'reflection': 0.5 },
{ 'center': np.array([-0.3, 0, 0]), 'radius': 0.15, 'ambient': np.array([0, 0.1, 0]), 'diffuse': np.array([0, 0.6, 0]), 'specular': np.array([1, 1, 1]), 'shininess': 100, 'reflection': 0.5 },
{ 'center': np.array([0, -9000, 0]), 'radius': 9000 - 0.7, 'ambient': np.array([0.1, 0.1, 0.1]), 'diffuse': np.array([0.6, 0.6, 0.6]), 'specular': np.array([1, 1, 1]), 'shininess': 100, 'reflection': 0.5 }
]
image = np.zeros((height, width, 3))
for i, y in enumerate(np.linspace(screen[1], screen[3], height)):
for j, x in enumerate(np.linspace(screen[0], screen[2], width)):
#
pixel = np.array([x, y, 0])
origin = camera
direction = normalize(pixel - origin)
color = np.zeros((3))
reflection = 1
for k in range(max_depth):
#
nearest_object, min_distance = nearest_intersected_object(objects, origin, direction)
if nearest_object is None:
break
intersection = origin + min_distance * direction
normal_to_surface = normalize(intersection - nearest_object['center'])
shifted_point = intersection + 1e-5 * normal_to_surface
intersection_to_light = normalize(light['position'] - shifted_point)
_, min_distance = nearest_intersected_object(objects, shifted_point, intersection_to_light)
intersection_to_light_distance = np.linalg.norm(light['position'] - intersection)
is_shadowed = min_distance < intersection_to_light_distance
if is_shadowed:
break
illumination = np.zeros((3))
# ambiant
illumination += nearest_object['ambient'] * light['ambient']
# diffuse
illumination += nearest_object['diffuse'] * light['diffuse'] * np.dot(intersection_to_light, normal_to_surface)
# specular
intersection_to_camera = normalize(camera - intersection)
H = normalize(intersection_to_light + intersection_to_camera)
illumination += nearest_object['specular'] * light['specular'] * np.dot(normal_to_surface, H) ** (nearest_object['shininess'] / 4)
# reflection
color += reflection * illumination
reflection *= nearest_object['reflection']
origin = shifted_point
direction = reflected(direction, normal_to_surface)
image[i, j] = np.clip(color, 0, 1)
print("%d/%d" % (i + 1, height))
plt.imsave('image.png', image)
?
, . . :
, , , , ;
. POO , ;
, (, ) ;
;
-. , «» . «» , 2D- 3D-: .
. :
Kotlin ( , Python) GitHub.