Le 19 décembre 2020, un article «Explication intuitive de l'intégrale» a été publié sur Habré .
Dans les commentaires, certains utilisateurs ont indiqué que l'explication n'était pas très intuitive, par exemple:
«Le sujet en lui-même est intéressant, j'ai récemment répété le cours, mais je dois dire qu'à mon avis, il n'y a pas de zeste dans le matériel. L'auteur a raison de dire que dans les publications modernes, les sujets sont souvent donnés sans description de leur application appliquée, c'est pourquoi la signification de leur étude n'est pas claire.
Mais spécifiquement, les intégrales sont un sujet qui doit être décrit soit plus court que le vôtre, soit beaucoup plus long.
Sinon, l'étudiant ne comprendra pas, et ceux qui savent ne découvriront rien de nouveau. "
J'essaierai de présenter le matériel aussi court et simple que possible. Pour que les élèves comprennent enfin, mais avec l'aide de leurs parents. Alors:
Je vis dans un avion et mon monde ressemble à ceci:

Tous mes mouvements sont limités à une ligne droite, que j'appelle «l'axe des abscisses» et le désigne par la lettre latine x . Ainsi, je peux marcher du point indiqué par le chiffre zéro (où se trouve ma maison), vers la droite vers l'infini et inversement, vers zéro. Les chiffres en abscisse me permettent de savoir à quelle distance de chez moi je suis. Je suis maintenant à 10 divisions de lui.
, , , , : -1, -2 . ., . , , .
- , , , «». , , , . . (), :
: , ?
: , .
: ?
: — .
: «»? , , .
: «» , ( ) . , . — . , . , «» - .
, , , :

() . ...
: , «»?
: , , ? , 6 . . , , 8. . , . , «» ( ) .
(6, 8). — , — . .
, (.., 13,5 13.5) , .
: , ?
: :
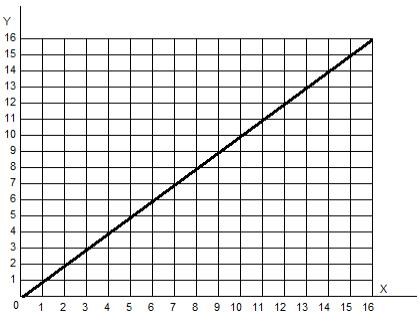
, , .

(4, 4) (10, 10), 6 . , 6 (). . , 6 .
- (, ), d (). dy, — dx. , , d = 6, dx = 6.
(dy/dx), : 6 / 6 = 1.
. = 1*.
, , . , , , 15, 15. — , , .
, , , , , -, - (0, 0). -, , . . :

, , , . , . ( ), , , 10. , , , 10 . , ( ) 5 . 10 5, 2. — — . ?
: , . , , , (5/10), 0.5, 1/2. ?
: ! () . , . ( ) , . — . 2, , , 0.5. , , = 2 = 0.5.
. , - , ( ), - , , . . , = 12 , = 0.5, , 12 , , 6.
, , : f(x) = x. , . , , f(x) = 2x f(x) = 0.5x. , ?
: . ?
: . , , () = x2, f(x) = x2. , .
, () . = x2 1, 2, 3 .. . 1:
y = 2 = 12 = 1.
, , 1, 1. :

, 2:
y = x2 = 22 = 4.
, (2, 4). 3 4, (3, 9) (4, 16) . :

, :

y = x2. , , = 1,5, , 1,5 . , (1.5, 2.25). , , ( ).
: - , . , , . , , . :

, ( (0, 0)), (3, 9). 9 , , 3 . , : 9 / 3 = 3. , , , 3. , 3, , , , , ! . . ? , , ? .
, - . , , — . , . , .
f(x) = x2 : , , . , 1: f '(x) = 2x.
f: f '(x) — , . .
? - f(x) = x2? . , , . , , , 1 . , :
f '(x) = 2x = 2*1 = 2.
1 .
4 ( = 4)? f '(x) = 2x = 2*4 8.
, 4 8. , , . ( ).
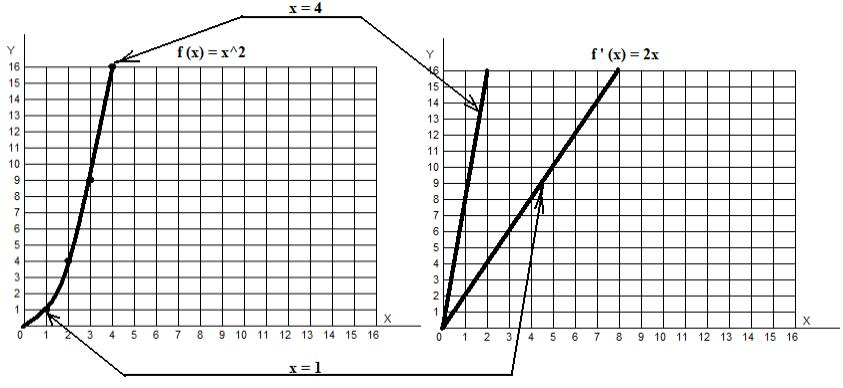
— , — , . , , . « , ».
f (x) = x.

: , ( , 1). , . , (, ( ) 1).
f(x) = x. : f '(x) = 1. ? , 1. , dx, dy . , , .
, ( ) . ?
, f(x) = 5. , ( ) 5, , dy ( ) .

, , , . , (dy/dx = 0/dx = 0).
: (, ), . , , .
: , : , — . , ?
: . . () , .
: , ? , f(x) = 5, :

, 5, , : 10 - 3 = 7. , 7, , 5 * 7 = 35 . 35 .
, ( ) .
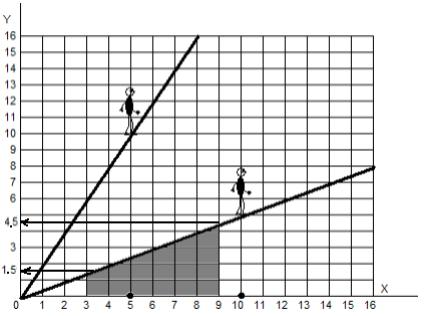
, , : 9 - 3 = 6.
: . ( ) , :
(1.5 + 4.5) : 2 = 3. — . 18. , 18 , ? , y = x2?

, 4 - 1 = 3 , ? 1 16, ? ?
: . «». , f (x) = x2 : f '(x) = 2x.
, , . , , . , , , , — .
(),
f(x) = x2 => f '(x) = 2x,
: , , : f '(x) = 2x => f(x) = x2 . . , , .
, ,
f (x) = x2 + 4:
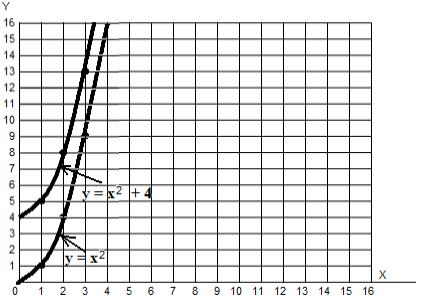
, f (x) = x2 , . , , , f (x) = x2 ! , f '(x) = 2x. () .
: ?
: , . , () ? , , 3 . ! , . , , . .
— , . , f (x) = x2 f (x) = x2 + 4 f '(x) = 2x.
: , , , , f (x) = x2 + 5 f (x) = x2 + 1.3 f (x) = x2 - 2 ? , , , ?
: , . f (x) = 2x F (x) = x2 + C, . , . , , , = 0. , , 4 .
, F — (), «» , , .
, F (x) = x2 + C, . :

f (x) = x2. , . 2, , x3. ( ). F (x) = x3/3 + .
.

, — 4 ( ):
F (x) = x3/3 = 43/3 = 21 1/3 ( )
:
F (x) = x3/3 = 13/3 = 1/3 ( )
: 21 1/3 - 1/3 = 21
21 . .
. , () f(x), .
() - , f '(x), , . , ( ) , .
, F, , , , . .
: ? , f (x) = x2 f (x) = x2 + 4, , ?
S: Ne vous inquiétez pas, lors de la recherche de l'intégrale de la deuxième fonction, la constante 4 dans sa primitive se transformera en 4x , par conséquent, un rectangle d'une hauteur de 4 cellules sera ajouté à la zone en dessous et il n'y aura pas d'erreur . Alors quelle route choisissez-vous?