Illustration: Daniel Grizely / Getty Images
C'est amusant de réfléchir à la façon dont nous apprenons quelque chose. Par exemple, la masse du Soleil est d'environ 2 x 10 30 kg. C'est un nombre tellement énorme qu'il est difficile de le comprendre. Et s'il nous est si difficile d'imaginer un si grand nombre, comment allons-nous rechercher ces valeurs? Eh bien, la méthode originale consistait à utiliser de petites masses, un bâton et une corde. C'est peut-être l'une des étapes importantes pour déterminer la masse du Soleil et de toutes les planètes de notre système solaire. Il s'agit d'une expérience Cavendish lancée par Henry Cavendishen 1798. L'expérience est vraiment cool, je vais donc vous expliquer comment cela fonctionne.
Il y a une attraction gravitationnelle entre les objets de masse. Le ballon de basket a une interaction gravitationnelle avec la Terre (car ils ont tous les deux une masse). C'est cette interaction gravitationnelle qui fait accélérer le ballon lorsqu'il touche le sol si vous le relâchez. Naturellement, tout le monde a toujours su que si vous lâchiez un objet, il tomberait. Cependant, ce n'est qu'à l'époque de Newton que les gens ont réalisé que cette attraction agit également entre des objets astronomiques tels que la Terre, la Lune et le Soleil. Cela nous donne un modèle pour l'interaction des forces, souvent appelée loi de la gravité de Newton, mais comme la plupart des grandes idées, elle doit avoir eu de nombreux co-auteurs.
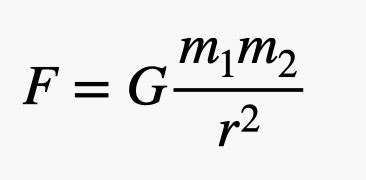
Art par: RHETT ALLAIN
Jetons un coup d'œil à ce modèle de force gravitationnelle. Premièrement, l'amplitude de cette force dépend du produit de deux masses en interaction (m 1 et m 2 ). Deuxièmement, la valeur diminue proportionnellement au carré de la distance entre les deux objets (r). Enfin, il y a G. C'est la constante gravitationnelle universelle. C'est la clé pour déterminer la masse de la terre.
Alors prenons un peu de recul pendant un moment. Lorsque nous mesurons des choses, nous devons toujours faire un choix. Si nous voulons obtenir la masse en kilogrammes, nous devons décider comment indiquer la valeur de 1 kg. On peut dire qu'un kilogramme est la masse d'un litre d'eau. Bien sûr, ce n'est pas la meilleure définition (nous avons maintenant de meilleures méthodes). D'accord, que diriez-vous de mesurer la force? Nous utilisons une unité appelée Newton, où 1 Newton est la force nécessaire pour accélérer un corps pesant 1 kilogramme sur 1 mètre par seconde au carré. Oui, la situation devient incontrôlable, mais l'essentiel est que vous puissiez donner ces définitions et tracer une unité de mesure sur une autre.
Imaginez maintenant cette expérience. Supposons que je prenne un litre d'eau (dont je sais qu'il fait 1 kilogramme) et que je mesure la force gravitationnelle provenant de la Terre. Si je connais le rayon de la Terre (les Grecs ont fait un excellent travailavec son calcul) et la constante gravitationnelle G, alors je peux résoudre l'équation de la force gravitationnelle pour la masse de la Terre (voir ci-dessus). Mais quelle est la constante gravitationnelle? C'est la partie la plus délicate, et c'est ainsi que vous pouvez trouver la valeur G.
Il s'avère que cette constante gravitationnelle est très petite. Cela signifie que l'attraction entre deux objets courants, tels que les bouteilles d'eau, est ridiculement petite. La seule façon d'obtenir une force gravitationnelle notable est si l'une des masses en interaction est énorme (comme la Terre). Cependant, il existe un moyen de le comprendre - utiliser un équilibre de torsion.
Commençons par une simple démo de physique que vous pouvez essayer chez vous. Prenez un crayon et placez-le sur le bord de la table de manière à ce qu'environ la moitié du crayon pende sur le bord, comme s'il était sur le point de tomber, mais tient. À ce stade, le crayon est essentiellement en équilibre sur le bord de la table. Le crayon ne supporte que ce petit point de contact, de sorte que la force de frottement ne peut pas induire un couple pour l'empêcher de tourner. Même une très petite pression sur l'extrémité du crayon le fera tourner. Il vous suffit de souffler pour que le crayon commence à tourner.

Vidéo: RHETT ALLAIN
J'aime amener mes doigts sur le crayon et faire semblant d'utiliser mes pouvoirs de super-héros pour le déplacer. Maintenant, remplaçons le crayon par un bâton plus long, et au lieu de le placer sur la table, je l'accrocherais à une ficelle. Puisqu'il repose au milieu, une infime quantité de force suffit à le faire tourner, comme avec un crayon. Au lieu de souffler, nous pourrions faire bouger une petite force gravitationnelle. Voilà comment cela fonctionne.
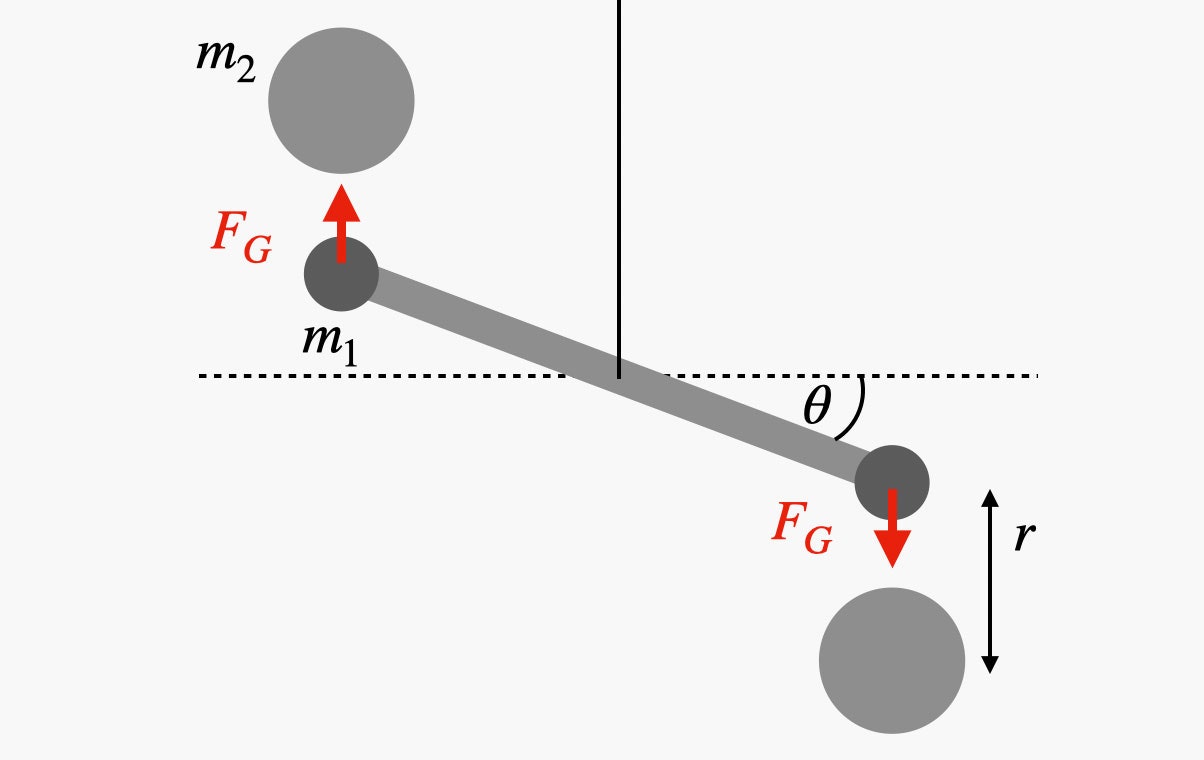
Illustration: RHETT ALLAIN
Il y a deux masses plus petites à l'extrémité de la barre horizontale rotative (étiquetées m 1 ). Ces masses interagissent avec de grandes masses (m 2) qui sont à une distance (r) d'eux. La barre horizontale atteindra finalement une certaine position d'équilibre car peu de couple est généré par la torsion du câble qui supporte la barre. Le câble agit comme un ressort rotatif. Plus il se tord, plus le couple est important. Si vous connaissez la relation entre l'angle de rotation (θ) et le couple, vous pouvez calculer la force gravitationnelle qui tire la masse à l'extrémité du manche vers la masse stationnaire la plus grande. Dans la configuration du diagramme ci-dessus, des masses importantes feront tourner le manche dans le sens des aiguilles d'une montre (vu du dessus). Si vous déplacez plus de masses de l'autre côté du bâton, les forces gravitationnelles le feront tourner dans le sens antihoraire. Cela montre que la rotation est due à l'interaction gravitationnelle entre les masses appariées.Une fois que le bâton prend une position stable, il ne reste plus qu'à mesurer les masses et la distance qui les sépare afin d'obtenir la constante gravitationnelle.
Dans ce cas, nous obtenons la constante gravitationnelle G = 6,67 x 10 -11 N * m 2 kg 2 . Vous pouvez voir que cette constante est vraiment très petite. À titre d'exemple, nous pouvons montrer comment le calcul est effectué. Supposons que vous soyez une personne se tenant à une distance de 1 mètre d'une autre personne de même masse (environ 75 kg). Quelle quantité de force agira sur vous en raison de l'attraction gravitationnelle? En substituant ces valeurs (avec la constante) dans l'équation de force, nous obtenons:
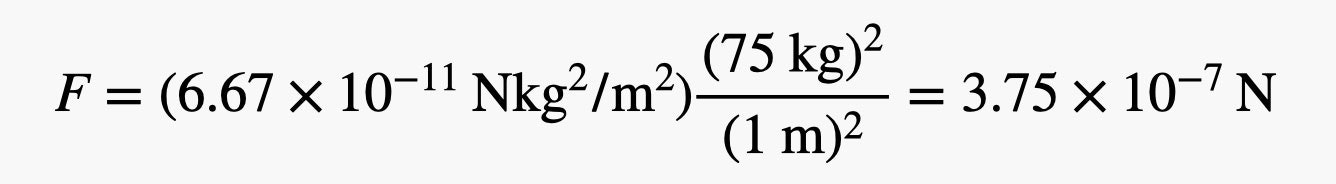
Illustration: RHETT ALLAIN
Mais cela n'a pas de sens. Personne ne peut ressentir si peu de puissance. Essayons d'imaginer une situation avec une force comparable à l'attraction gravitationnelle entre deux personnes. Comment tu aimes ça? Supposons que vous placiez un petit objet dans votre main. Vous pouvez sentir la force gravitationnelle de la Terre sur cet objet parce que votre main doit le pousser vers le haut pour équilibrer la force gravitationnelle. Quel objet de masse créera une force gravitationnelle causée par la Terre, égale à la force d'attraction entre deux personnes? À la surface de la Terre, certaines de ces valeurs sont toujours les mêmes (constante gravitationnelle, masse de la Terre et distance au centre de la Terre). Nous pouvons regrouper toutes ces valeurs en un seul nombre.
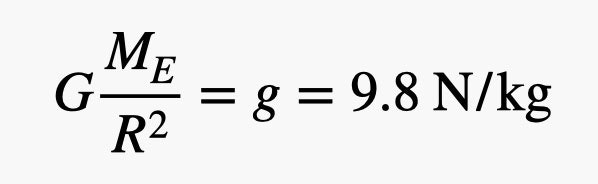
Art par: RHETT ALLAIN
Nous pouvons appeler cela la constante gravitationnelle locale de la Terre. Tout ce que vous avez à faire est de prendre la masse et de la multiplier par "g" (nous utilisons un "g" minuscule pour éviter toute confusion avec une autre constante gravitationnelle "G") et vous obtenez la force gravitationnelle (poids). Dans ce cas, vous auriez besoin d'un objet d'environ 4 x 10-11 grammes pour obtenir un poids égal à la gravité entre deux personnes. C'est encore trop peu à comprendre. Et si oui? Les cheveux humains peuvent avoir une masse volumique linéaire de 6,5 grammes par kilomètre (informations tirées de cette publication ). Cela signifie seulement 6 x 10 -6 cheveux millimètres a un poids égal à l'attraction entre deux personnes. C'est incompréhensible pour l'esprit. Voici un bonus, mes calculs , si vous souhaitez modifier les valeurs.
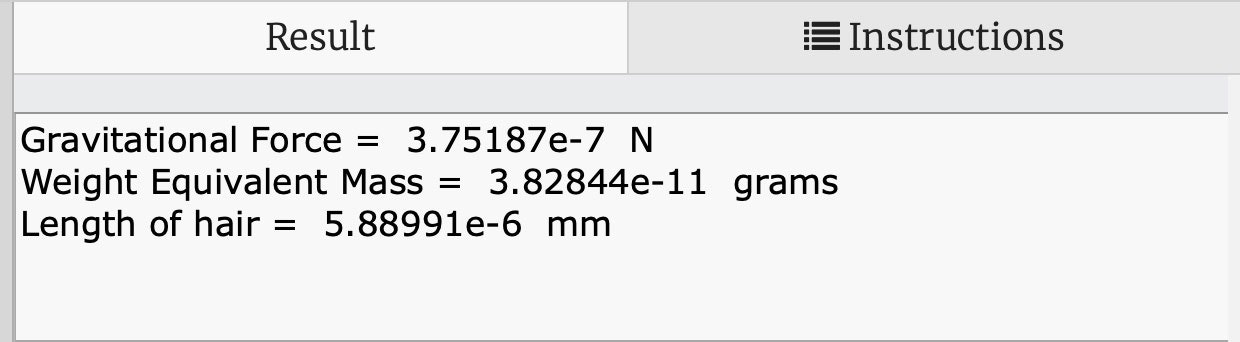
Illustration: RHETT ALLAIN
Oh oui, vous pouvez refaire le même calcul, mais utilisez une masse connue et calculez la masse de la Terre. Cela représente environ 5,97 x 10 24 kilogrammes. Mais pourquoi s'arrêter là? Vous pouvez également utiliser la valeur G pour trouver la masse du soleil. Je vais expliquer brièvement comment fonctionne ce calcul.
Donc, vous avez une planète comme Mercure qui tourne autour du Soleil. Si nous prenons en compte le fait que l'orbite est circulaire, alors la force gravitationnelle du Soleil agit sur Mercure.
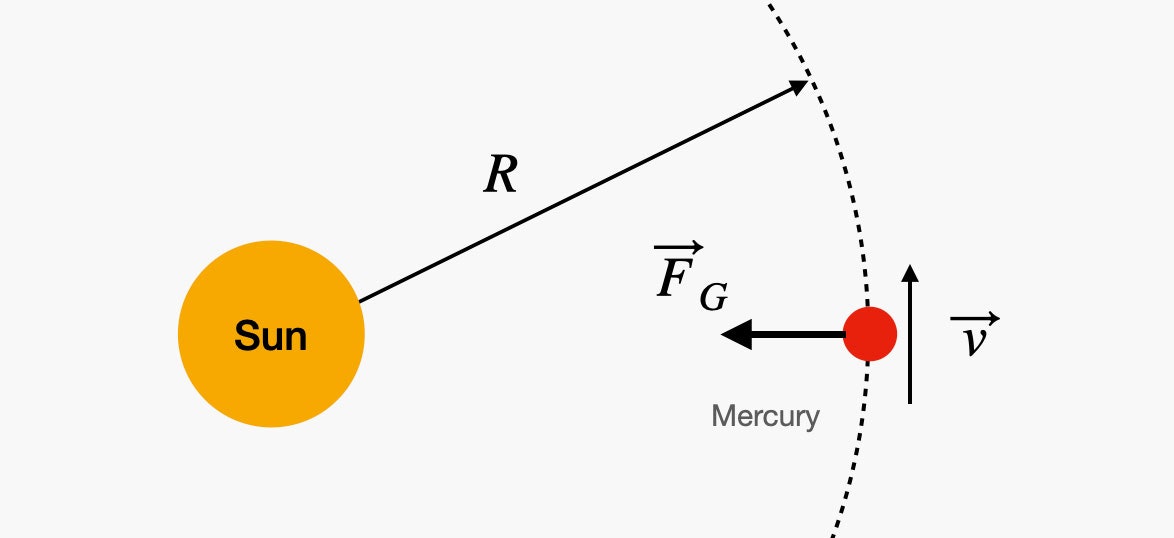
Art par: RHETT ALLAIN
La force gravitationnelle fait que la planète accélère et se déplace en cercle (accélération centripète). Mais cette accélération centripète dépend à la fois de la vitesse angulaire (ω) et de la distance orbitale (R). Puisqu'il n'y a qu'une seule force agissant sur la planète (force gravitationnelle), elle sera égale à la masse multipliée par l'accélération, et le résultat sera le rapport suivant.
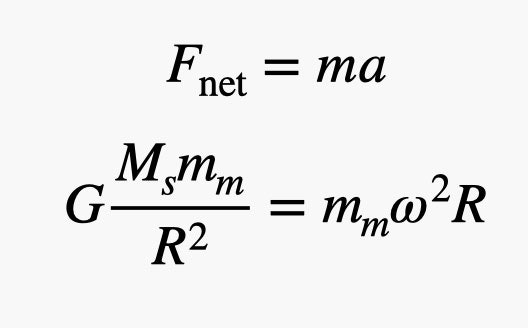
Illustration: RHETT ALLAIN
Notez que le soleil est supposé stationnaire ici, ce qui est généralement correct. La masse du Soleil est colossale par rapport à la masse de Mercure, donc la masse de Mercure n'a pas d'importance. Donc, la solution pour trouver la masse du soleil:
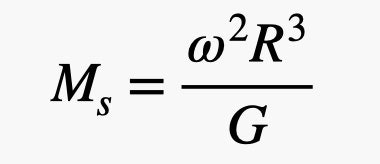
Illustration: RHETT ALLAIN
Il ne vous reste plus qu'à trouver la distance entre le point de l'orbite et le centre de Mercure. Vous pouvez le faire en commençant par le rayon de la Terre . Ensuite, vous devez trouver la vitesse angulaire - vous pouvez l'obtenir en regardant combien de temps il faut à Mercure pour effectuer une révolution autour du Soleil. Après cela, tout est prêt. Vous avez une constante gravitationnelle et vous pouvez calculer la masse du soleil. C'est incroyable que tout commence par de petites masses sur un bâton tournant horizontalement, mais c'est vrai.