Dans un travail récent, un nouveau record de vitesse a été établi pour la multiplication de deux matrices . Cela marque également la fin d'une époque pour la méthode que les scientifiques ont utilisée pour la recherche pendant des décennies.
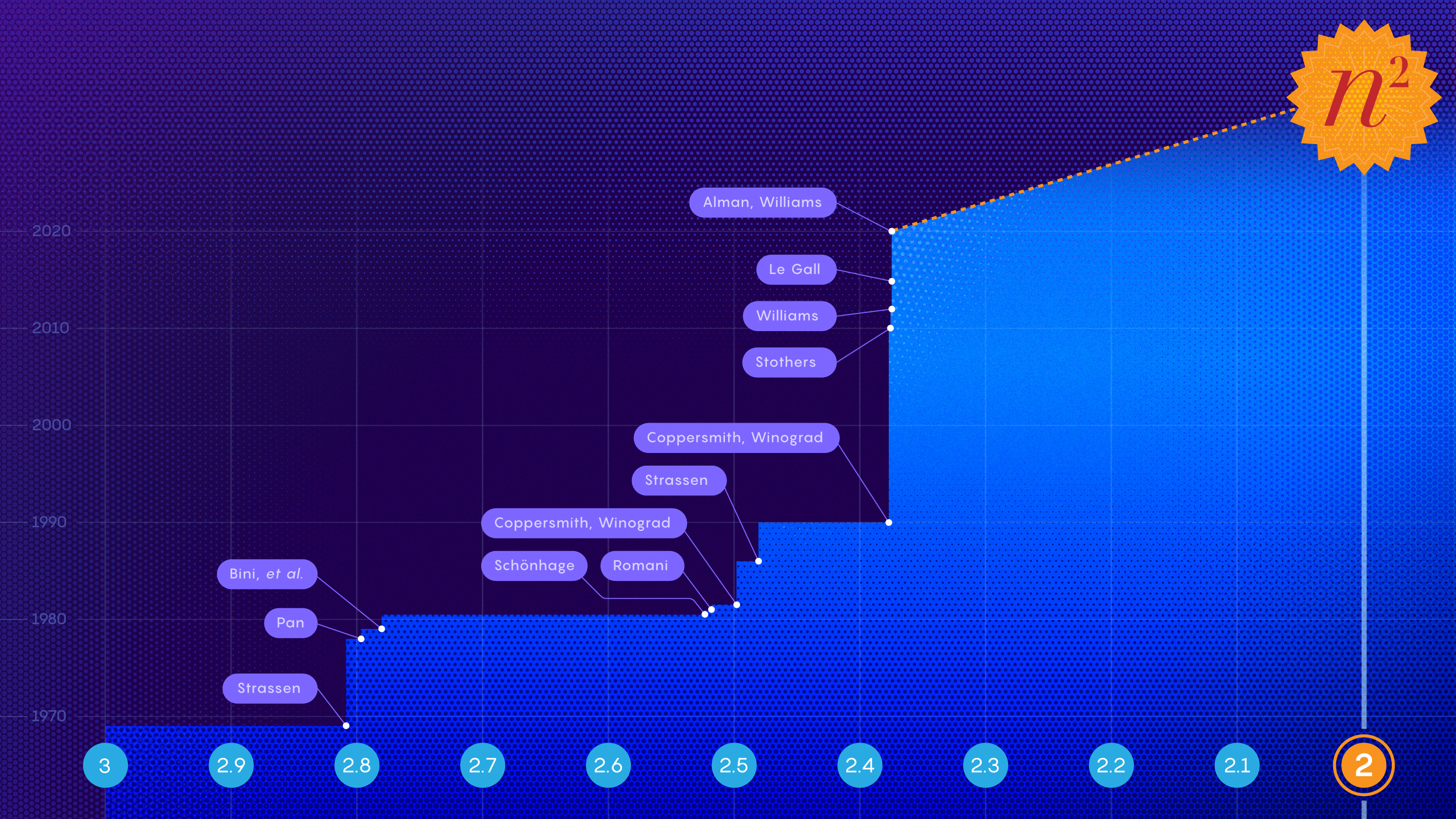
Les mathématiciens s'efforcent d'atteindre un objectif mythique - le deuxième degré (exposant deux), c'est-à-dire multiplier une paire de n x n matrices en seulement n 2 étapes. Les chercheurs se rapprochent de leur objectif, mais pourront-ils jamais l'atteindre?
Pour les informaticiens et les mathématiciens, l'idée même du «second degré» est associée à l'idée d'un monde parfait.
«Il est difficile de faire la distinction entre la pensée scientifique et la rêverie sans fondement», admet Chris Umans du California Institute of Technology. "Je veux que le diplôme soit deux parce que c'est beau."
Du point de vue du nombre d'étapes requis, le "second degré" est la vitesse d'exécution idéalel'une des opérations mathématiques les plus fondamentales est la multiplication matricielle. Si le deuxième degré est réalisable, alors la multiplication matricielle peut être effectuée aussi rapidement que physiquement possible. Si ce n'est pas le cas, alors nous sommes coincés dans un monde qui ne correspond pas à nos rêves.
Les matrices sont des tableaux de nombres. Lorsque les deux matrices concordent (le nombre de colonnes dans le premier facteur est égal au nombre de lignes dans le second), elles peuvent être multipliées pour obtenir le troisième. Par exemple, si vous commencez avec une paire de matrices 2 x 2, leur produit sera également une matrice 2 x 2 contenant quatre éléments. Plus généralement, le produit d'une paire de n x n matrices est une autre matrice n x n à n 2 éléments.
Par conséquent, le plus petit nombre d'étapes possible pour multiplier des paires de matrices est n 2 , c'est-à-dire le nombre d'étapes nécessaires juste pour écrire la réponse. D'où le nom de «deuxième degré».
Et même si personne ne sait avec certitude si cela peut être réalisé, les chercheurs continuent à avancer dans cette direction.
L'article, publié en octobre, se rapproche encore plus de l'objectif et décrit la méthode la plus rapide pour multiplier deux matrices à ce jour. Le résultat reçu par Josh Alman , doctorant à l'Université Harvard, et Virginia Wasilewska Williamsdu Massachusetts Institute of Technology, diminue le degré du meilleur précédent d'environ cent millième. C'est vraiment une grande réussite dans ce domaine, obtenue grâce à un travail minutieux.
Pour mieux comprendre ce processus et comment il peut être amélioré, commençons par une paire de matrices 2 x 2, A et B.Lors du calcul de chaque élément de leur produit, vous utilisez la ligne correspondante de A et la colonne correspondante de B.Pour obtenir l'élément en haut à droite, multipliez le premier nombre de la première ligne A par le premier nombre de la deuxième colonne B, puis multipliez le deuxième nombre de la première ligne A par le deuxième nombre de la deuxième colonne B et ajoutez les deux produits.

Samuel Velasco / Quanta Magazine
Cette opération est connue sous le nom de obtenir un "produit scalaire" d'une ligne avec une colonne (parfois appelé "produit interne"). Pour calculer d'autres éléments dans le produit matriciel, répétez la procédure avec les lignes et colonnes correspondantes.
En général, la méthode classique de multiplication matricielle 2 x 2 consiste en huit multiplications et plusieurs additions. En règle générale, cette méthode de multiplication de deux n x n matrices nécessite n 3 multiplications.
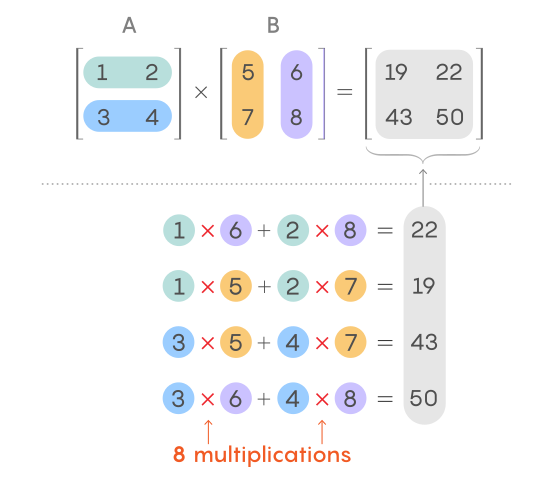
À mesure que la taille des matrices augmente, le nombre de multiplications nécessaires pour trouver leur produit augmente beaucoup plus rapidement que le nombre d'ajouts. Pour trouver le produit de matrices 2 x 2, il suffit de huit multiplications intermédiaires, et pour trouver le produit de matrices 4 x 4, il y en a déjà 64. Cependant, le nombre d'additions nécessaires pour obtenir la somme de ces matrices est pas si différent. Habituellement, le nombre d'additions est égal au nombre d'éléments dans la matrice, c'est-à-dire quatre pour les matrices 2 x 2 et 16 pour les matrices 4 x 4. Cette différence entre l'addition et la multiplication montre clairement pourquoi les chercheurs mesurent la vitesse de multiplication de la matrice uniquement en termes de nombre de multiplications nécessaires.
"Les multiplications sont tout", dit Umans. "L'exposant à la fin dépend entièrement du nombre de multiplications. Les ajouts disparaissent en un sens. "
Pendant des siècles, les gens ont cru que le n 3 était le moyen le plus rapide de multiplier les matrices . En 1969, Volker Strassen aurait tenté de prouver qu'il était impossible de multiplier 2 x 2 matrices en utilisant moins de huit multiplications. Apparemment, il n'a toujours pas pu trouver de preuves, et après un certain temps, il a compris pourquoi: en fait, il existe un moyen de le faire en utilisant sept multiplications!
Strassen a proposé un ensemble complexe de relations qui lui ont permis de remplacer l'une de ces huit multiplications par 14 ajouts supplémentaires. La différence peut sembler une différence subtile, mais elle est payante car la multiplication contribue plus que l'addition. En trouvant un moyen de se débarrasser d'une multiplication pour de petites matrices 2 x 2, Strassen a découvert une possibilité qu'il pourrait utiliser lors de la multiplication de matrices plus grandes.
«Ce petit changement se traduit par d'énormes améliorations dans la gestion de grandes matrices», déclare Williams.


Virginia Wasilewska Williams du Massachusetts Institute of Technology et Josh Alman de l'Université de Harvard ont découvert le moyen le plus rapide de multiplier deux matrices en n 2,3728596 pas. Jared Charney; Richard T.K. faucon
Supposons que vous souhaitiez multiplier une paire de matrices 8 x 8. Une façon de faire est de diviser chaque grande matrice en quatre matrices 4 x 4 de sorte que chacune comporte quatre éléments. Étant donné que les éléments d'une matrice peuvent également être des matrices, vous pouvez considérer les matrices d'origine comme une paire de matrices 2 x 2, dont chacun des quatre éléments est lui-même une matrice 4 x 4. Avec quelques manipulations, chacune de ces 4 x 4 matrices peuvent être divisées en quatre matrices de taille 2 x 2.
L'idée derrière cette division multiple de grandes matrices en plus petites est que vous pouvez appliquer encore et encore l'algorithme de Strassen à des matrices plus petites et utiliser sa méthode pour réduire le nombre d'étapes à chaque étape. En général, l'algorithme de Strassen a augmenté la vitesse de multiplication de la matrice avec n 3 à n 2,81 étapes multiplicatives.
La prochaine étape importante dans le développement de l'idée a eu lieu à la fin des années 1970, lorsqu'une approche fondamentalement nouvelle pour résoudre ce problème est apparue. Il s'agit de traduire la multiplication matricielle en un autre problème d'algèbre linéaire informatique en utilisant des objets appelés tenseurs. Les tenseurs utilisés dans ce problème sont des tableaux tridimensionnels de nombres composés de nombreuses parties différentes, dont chacune ressemble à un petit problème de multiplication matricielle.
La multiplication matricielle et ce problème tenseur sont en un sens équivalents l'un à l'autre, mais les chercheurs disposaient déjà de procédures plus rapides pour résoudre ce dernier. Ainsi, ils ont été confrontés à la tâche de déterminer le "taux de change" entre eux: quelles matrices de taille peuvent être multipliées par les mêmes coûts de calcul que ceux nécessaires pour résoudre le problème des tenseurs?
«C'est un concept très courant en informatique théorique: transformer les tâches et faire des analogies entre elles pour montrer qu'elles sont tout aussi simples ou complexes», a déclaré Alman.
En 1981, Arnold Schönhage a utilisé cette approche pour prouver que la multiplication matricielle peut être effectuée en n 2 522 étapes. Strassen a appelé plus tard cette approche la «méthode laser» .
Au cours des dernières décennies, chaque amélioration de la multiplication matricielle est venue d'améliorations de la méthode laser, les chercheurs ayant trouvé des moyens plus efficaces de transformer le problème. Dans leur nouvelle preuve, Alman et Williams brouillent la distinction entre les deux problèmes et montrent qu'il est possible de réduire le nombre de multiplications. «Dans l'ensemble, Josh et Virginia ont trouvé un moyen d'appliquer l'informatique automatique à la méthode laser et ont obtenu les meilleurs résultats à ce jour», a déclaré Henry Cohn.de Microsoft Research.
Dans leur article, la limite théorique sur la vitesse de multiplication matricielle est améliorée à n 2,3728596 .
Grâce également à ces recherches, Williams peut retrouver la couronne dans le domaine de la multiplication matricielle, qu'elle a légitimement reçue en 2012 (n 2.372873 ), puis perdue en 2014 au profit de François Le Gall (n 2.3728639 ).
Mais, malgré toutes ces courses et victoires, il devient clair que dans le cas de cette approche, la loi des rendements décroissants, ou des rendements décroissants, opère. Très probablement, l'amélioration d'Alman et Williams a presque complètement épuisé les possibilités de la méthode laser, mais n'a pas permis d'atteindre le but théorique final.
«Il est peu probable que vous puissiez vous approcher du deuxième degré en utilisant cette famille de méthodes», a déclaré Umans.
Cela exigera la découverte de nouvelles méthodes et une forte conviction que cela est possible du tout.
Williams se souvient d'une de ses conversations avec Strassen à ce sujet: «Je lui ai demandé s'il pensait qu'il était possible d'obtenir le deuxième degré pour la multiplication matricielle, et il a répondu:« Non, non, non, jamais! ».