Pendant assez longtemps, je me suis battu avec l'arbre rouge-noir ( ci-après - kchd ). Toutes les informations que j'ai trouvées étaient dans l'esprit "les feuilles et la racine de l'arbre sont toujours noires PARCE QUE", "les 5 principales propriétés d'un arbre rouge-noir" ou "3 cas lors de l'équilibrage et 12 cas lors de la suppression d'un nœud". Cet arrangement ne me convenait pas.
Je ne voulais pas mémoriser les propriétés de l'arbre, le pseudocode et les options d'équilibrage, je voulais savoir pourquoi. Comment les couleurs aident-elles à équilibrer? Pourquoi un nœud rouge ne peut-il pas avoir un enfant rouge? Pourquoi la profondeur d'un arbre est-elle mesurée «hauteur noire»?
J'ai reçu des réponses à ces questions seulement lorsque j'ai reçu un lien vers une conférence sur deux ou trois arbres, par laquelle nous commencerons.
Cet article est divisé en 3 parties logiques. Je recommande de les lire dans l'ordre indiqué. La première partie (celle-ci) sera destinée à une introduction au ccd et à le connaître. Dans la deuxième partie, nous parlerons d'équilibrage et d'insertion dans ccd. Dans la troisième et dernière partie, nous analyserons le processus de suppression d'un nœud. Soyez patient et appréciez la lecture :)
Avertissement
Dans cet article, il n'y aura aucune information sur les avantages et les inconvénients de l'arbre, son application, etc.: il y a beaucoup d'informations sur les asymptotiques de l'arbre et son utilisation sur Internet.
Le matériel est destiné à ceux qui sont déjà familiers avec le ccd et qui veulent maintenant les comprendre, ainsi qu'à ceux qui commencent tout juste à les connaître.
L'article ne contiendra pas de détails sur la mise en œuvre de la structure.
— . .
-
- , -
, , - - , , , . - - .
- - , . - ( , ). 2-, - 3-. : . :
, .
- , - .
- - , .
, , 5. - 5 .

12. 12 (, ), "" ( , ), .. . 5-12.

. 17. . 5-12-17.
- , . ! "" . . 12, 5, - 17.
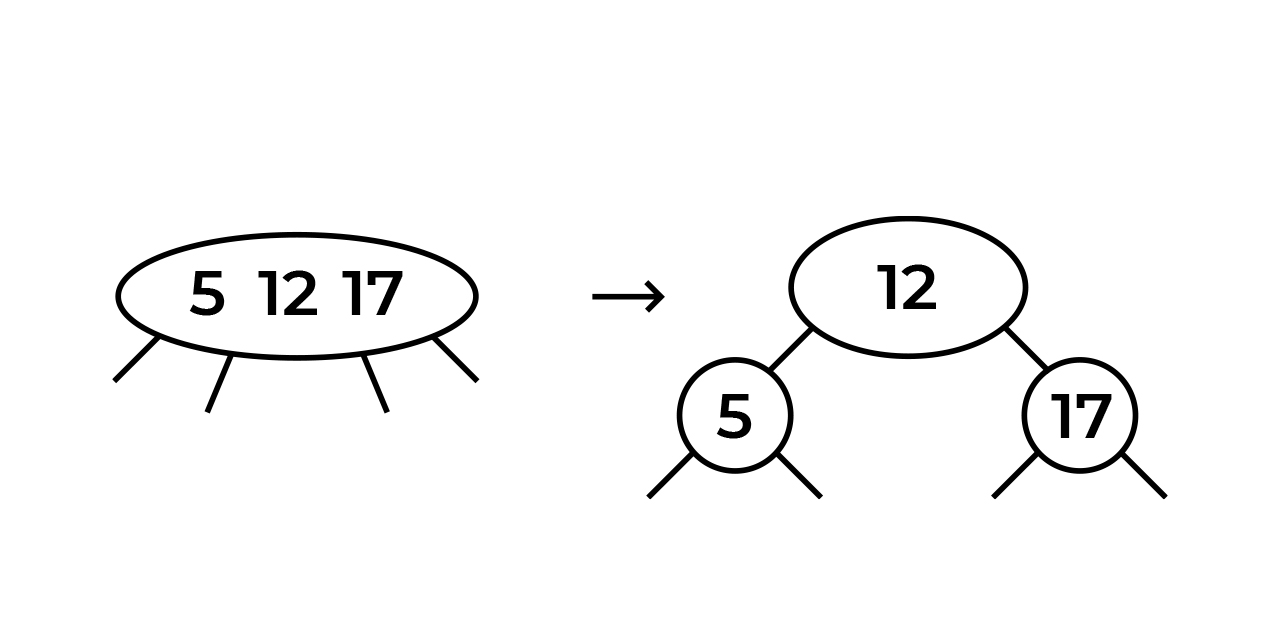
, , - . : , "" . 3 :
. , ( ).
. ( ).
. , .
.
, . 3. , . , 3 5. 3 5 . 3-5.
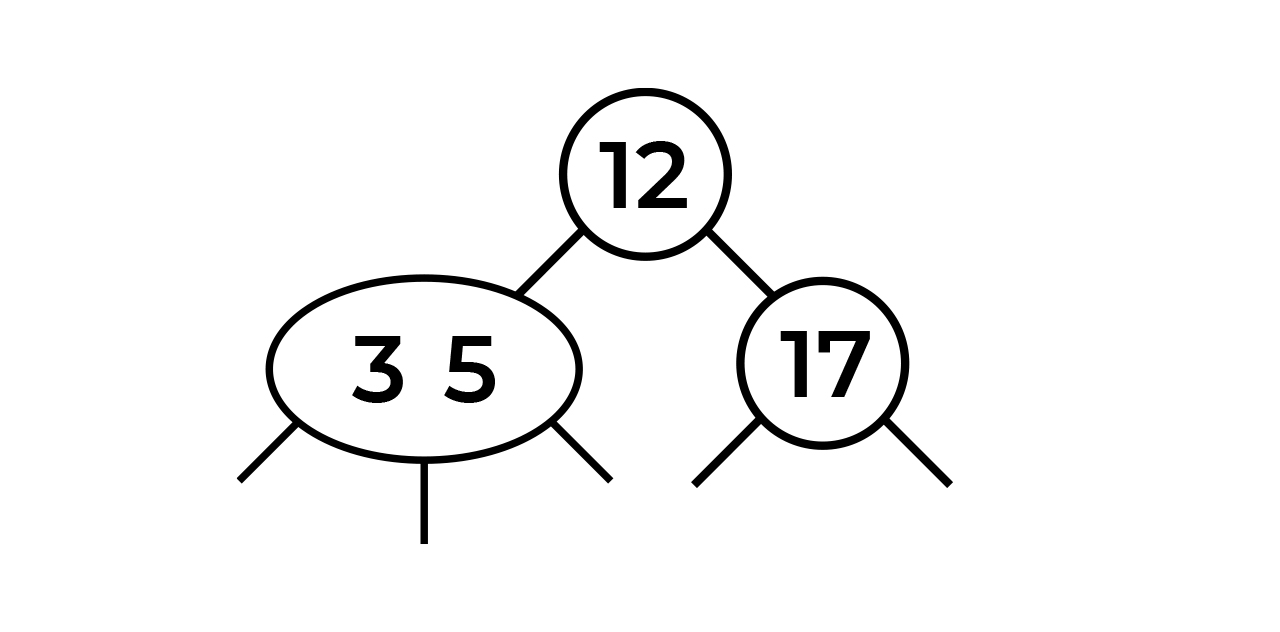
, :)
4 3-5. 3-4-5, , , . ? , .. "" 4 .
. , 4 , - , 4. 5. :
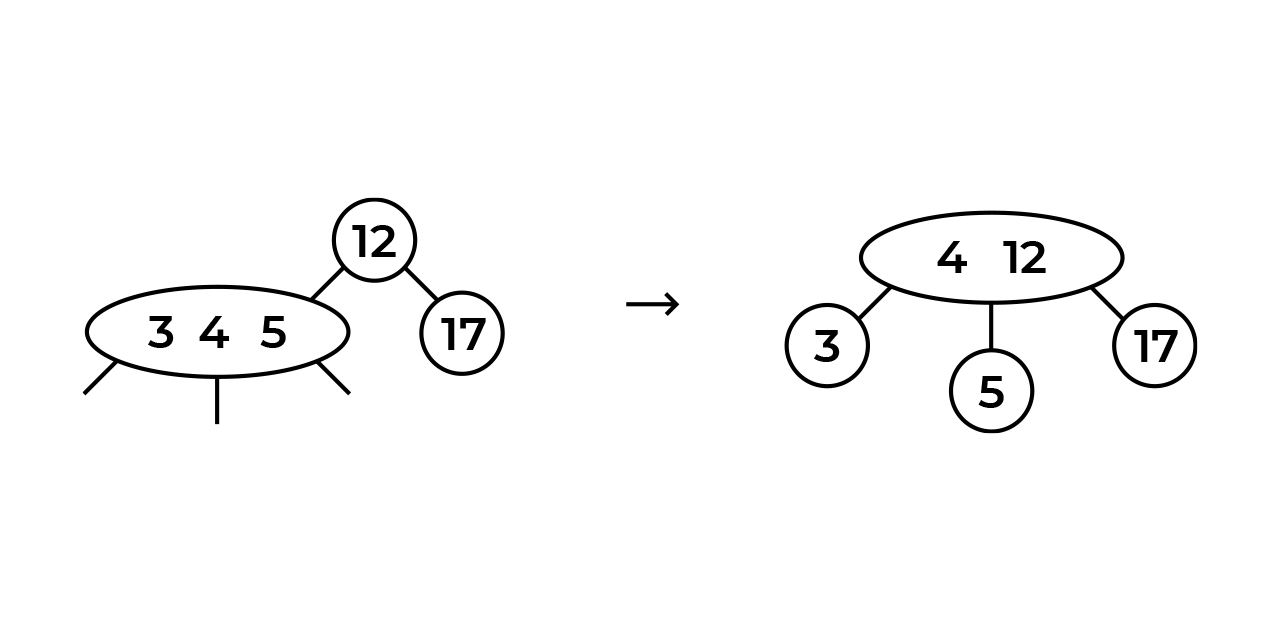
5 ? : - , - . 5 4, 5 , .. . 5 , "", 4-12 (, 5 , "" ).
, . :
, , .
, , , .
, , .
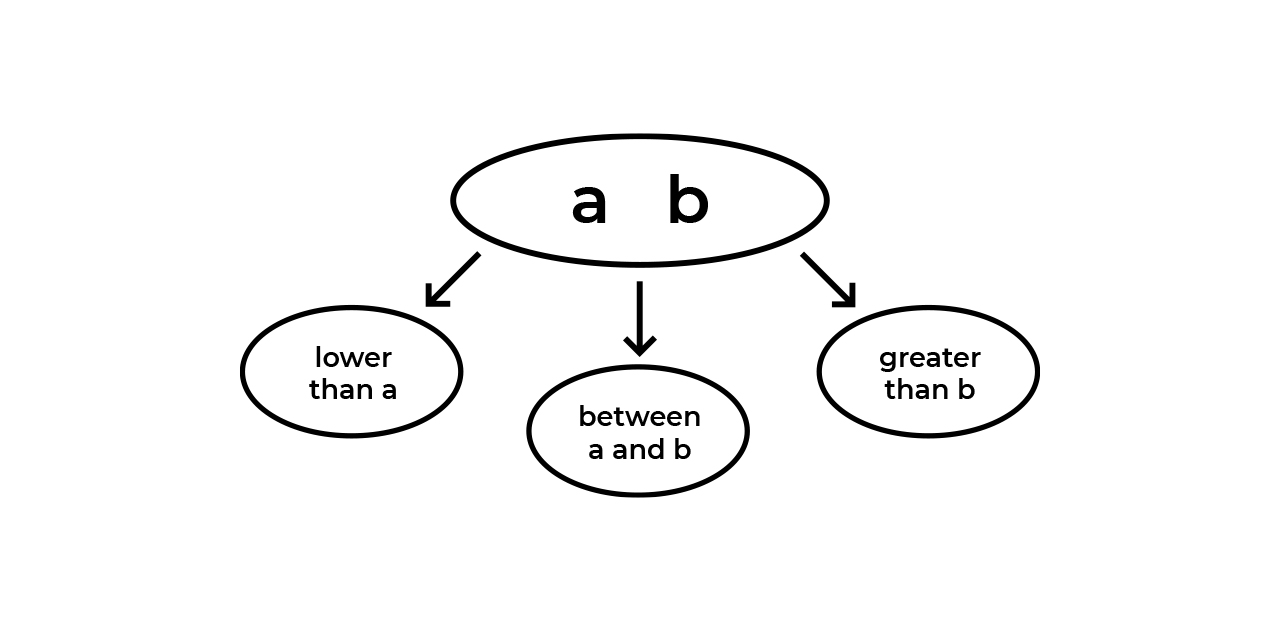
, . , , - . , - (, 4-5-12, , 5 4 12). , . , , ( , 7? 9?).
, , , . , , , . .
, , , . , , ( ). - .
-
, - - . - . ?
, 3-. 3- 2- . - , , , ( ), .
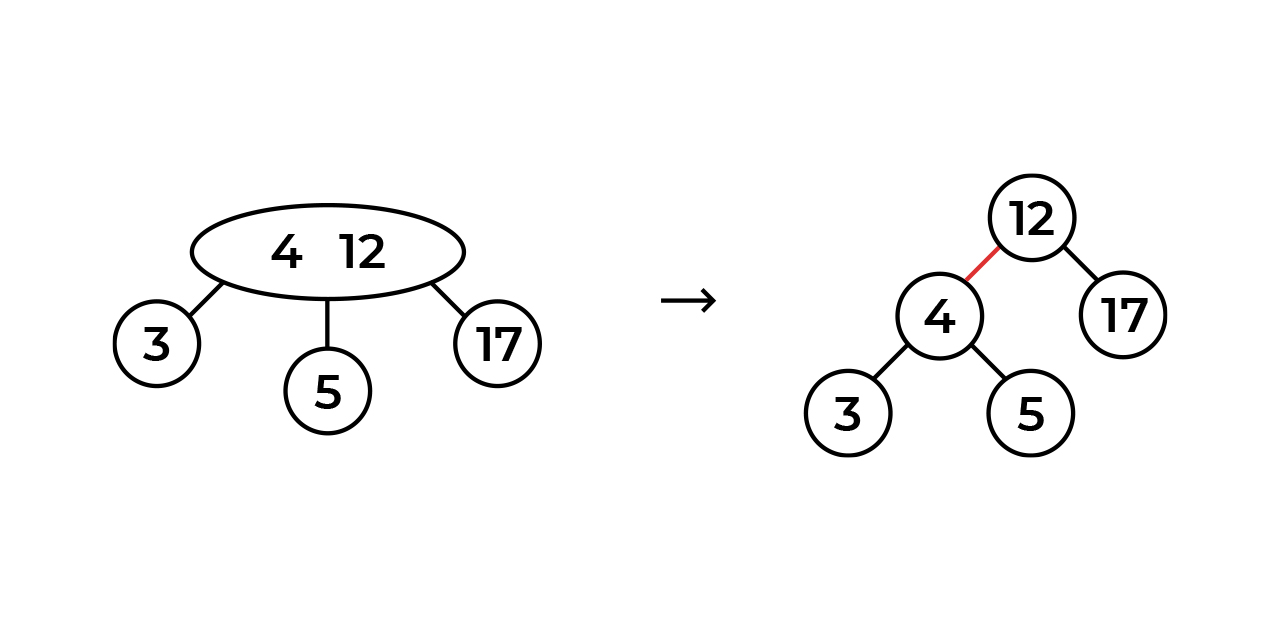
, , .
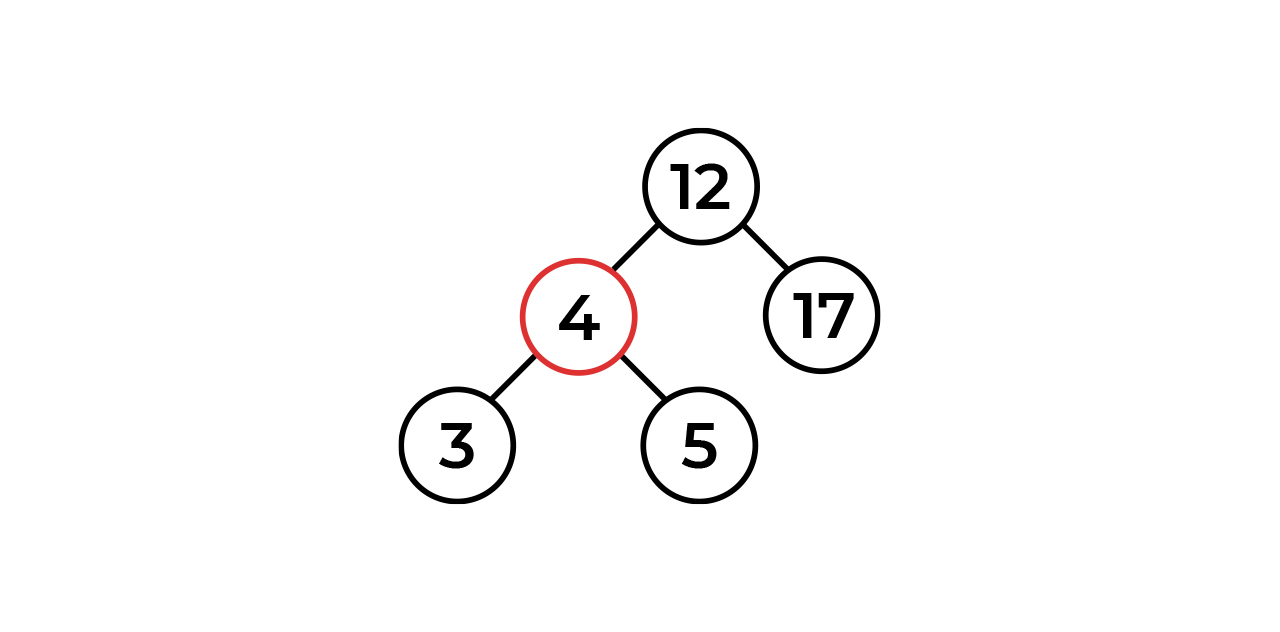
, - . , , ( , ).
-
, - , , 3- ( ). , , . , ( ).
1.
. , , - 3- 2-3 . , 4-, :)
2.
. , : .
3.
null- (, ) - . , . , , .
Puisque nous avons touché aux nœuds nuls, il faut dire que tous les nœuds de l'arbre doivent toujours avoir deux descendants, et si la référence au descendant est zéro, alors cela mène exactement au nœud nul. En fait, cela pose une question dans la mise en œuvre, il était plus pratique pour moi d'ajouter un nœud nul (moins de problèmes avec les itérateurs, l'équilibrage, etc.).
Propriété 4.
La hauteur de l'arbre est mesurée uniquement par des nœuds noirs et est appelée "hauteur noire". Là encore, tout devient en général évident: le nœud rouge n'est qu'un ajout au nœud noir, il en fait partie, donc la hauteur est considérée comme basée sur des nœuds noirs.
Ceci conclut l'introduction. Dans la partie suivante, nous parlerons de la façon d'insérer des nœuds dans un arbre et de l'équilibrer.