🚆 🔗 👩🏿‍🤝‍👨🏾 Python, corrélation et régression: partie 4 🚯 ⛱️ 🧒

Voir le post précédent ici .

Prédiction

Enfin, nous arrivons à l'une des applications les plus importantes de la régression linéaire: la prédiction . Nous avons formé un modèle pour prédire le poids des nageurs olympiques en fonction de leur taille, de leur sexe et de leur année de naissance.

Mark Spitz, 9 fois champion olympique de natation, a remporté 7 médailles d'or aux Jeux olympiques de 1972. Il est né en 1950 et, selon le site Wikipédia, mesure 183 cm et pèse 73 kg. Voyons ce que notre modèle prédit en termes de poids.

Notre modèle de régression multiple exige que ces valeurs soient fournies sous forme de matrice. Chaque paramètre doit être passé dans l'ordre dans lequel le modèle a appris les caractéristiques afin d'appliquer le coefficient correct. Après le biais, le vecteur de caractéristiques doit contenir la hauteur, le sexe et l'année de naissance dans les mêmes unités dans lesquelles le modèle a été formé:

La matrice β contient des coefficients pour chacune de ces caractéristiques:

La prédiction du modèle sera la somme des produits des coefficients β et des caractéristiques x dans chaque ligne:

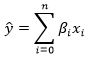
, β xspitz.

, :

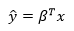
β^Tx — 1 × n n × 1. 1 × 1:

def predict(coefs, x): 
    ''' '''
    return np.matmul(coefs, x.values)

def ex_3_29():
    '''   '''
    df = swimmer_data()
    df['_'] = df[''].map({'': 1, '': 0}).astype(int) 
    df[' '] = df[' '].map(str_to_year)
    X = df[[', ', '_', ' ']] 
    X.insert(0, '', 1.0)
    y = df[''].apply(np.log) 
    beta = linear_model(X, y)
    xspitz = pd.Series([1.0, 183, 1, 1950]) #   
    return np.exp( predict(beta, xspitz) )

84.20713139038605

84.21, 84.21 . 73 . , , .

. , , . , , . ŷ , , μ. , , y^.

^{, , , . 95%- – , 95% . , 95%- – , 95%- .}

. , :

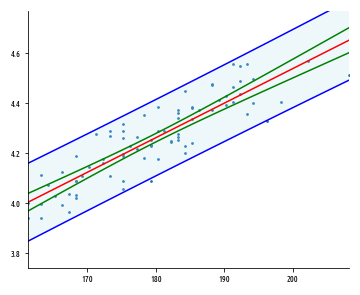
ŷ_p — , . t-, n - p, .. . , F-. , , , , , 95%- .

def prediction_interval(x, y, xp):
    '''  '''
    xtx    = np.matmul(x.T, np.asarray(x))
    xtxi   = np.linalg.inv(xtx)  
    xty    = np.matmul(x.T, np.asarray(y)) 
    coefs  = linear_model(x, y) 
    fitted = np.matmul(x, coefs)
    resid  = y - fitted
    rss    = resid.dot(resid)  
    n      = y.shape[0]  # 
    p      = x.shape[1]  # 
    dfe    = n - p 
    mse    = rss / dfe
    se_y   = np.matmul(np.matmul(xp.T, xtxi), xp)
    t_stat = np.sqrt(mse * (1 + se_y))         # t-
    intl   = stats.t.ppf(0.975, dfe) * t_stat   
    yp     = np.matmul(coefs.T, xp)
    return np.array([yp - intl, yp + intl])

t- , .

, se_y

t- t_stat

.

, , :

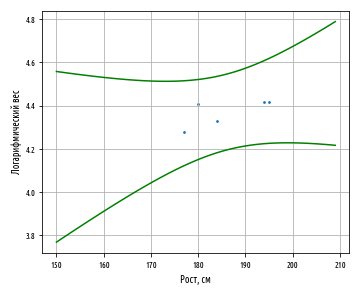
5 , 95%- . , :

def ex_3_30():
    ''' 
            '''
    df = swimmer_data()
    df['_'] = df[''].map({'': 1, '': 0}).astype(int) 
    df[' '] = df[' '].map(str_to_year)
    X = df[[', ', '_', ' ']] 
    X.insert(0, '', 1.0)
    y = df[''].apply(np.log) 
    xspitz = pd.Series([1.0, 183, 1, 1950])  #  .
    return np.exp( prediction_interval(X, y, xspitz) )

array([72.74964444, 97.46908087])

72.7 97.4 ., 73 ., 95%- . .

1950 ., 2012 . , , , . .

, . , , . , , . 1979 ., .

, 1972 . 22- 185 . 79 .

^{— .}

, , .

R², , . , .. , , , - .

β :

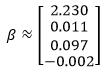
1972 . :

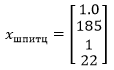
def ex_3_32():
    '''    
        '''
    df = swimmer_data()
    df['_'] = df[''].map({'': 1, '': 0}).astype(int) 
    X = df[[', ', '_', '']] 
    X.insert(0, '', 1.0)
    y = df[''].apply(np.log) 

    beta = linear_model(X, y)
    #    
    xspitz = pd.Series([1.0, 185, 1, 22]) 
    return np.exp( predict(beta, xspitz) )

78.46882772630318

78.47, .. 78.47 . , 79 .

Github. .

, . , r R² R̅². , ρ .

, Python. , pandas numpy . β, , . , .

Python, corrélation et régression: partie 4

Prédiction

More articles: