En remuant du sucre dans du thé ou du café le matin, vous remarquerez que la forme de la surface de l'eau dans le verre prend la forme d'un entonnoir. A propos de ce à quoi les gens pensent depuis longtemps, par exemple, il y a un article sur Habré , qui prétend qu'il s'agit d'un paraboloïde (une parabole, si vous regardez dans une section). Cependant, il est facile de voir qu'il ne s'agit pas vraiment d'une parabole. Ou plutôt, pas du tout une parabole. Et qu'est-ce que c'est alors ?
Afin de calculer la forme que prendra l'eau (ou autre liquide) dans le verre, il est nécessaire de prendre en compte la viscosité et l'effet des parois du verre. Par conséquent, ici, il est nécessaire d'utiliser les équations de Navier-Stokes pour un fluide incompressible visqueux. Étant donné que le verre a une forme cylindrique, les équations de Navier-Stokes doivent être écrites en coordonnées cylindriques, où l'axe z longe le centre du verre et est dirigé vers le haut, et r est la distance de cet axe. En général, les équations de Navier-Stokes en coordonnées cylindriques sont les suivantes (Landau-Lifshitz Hydrodynamics) :
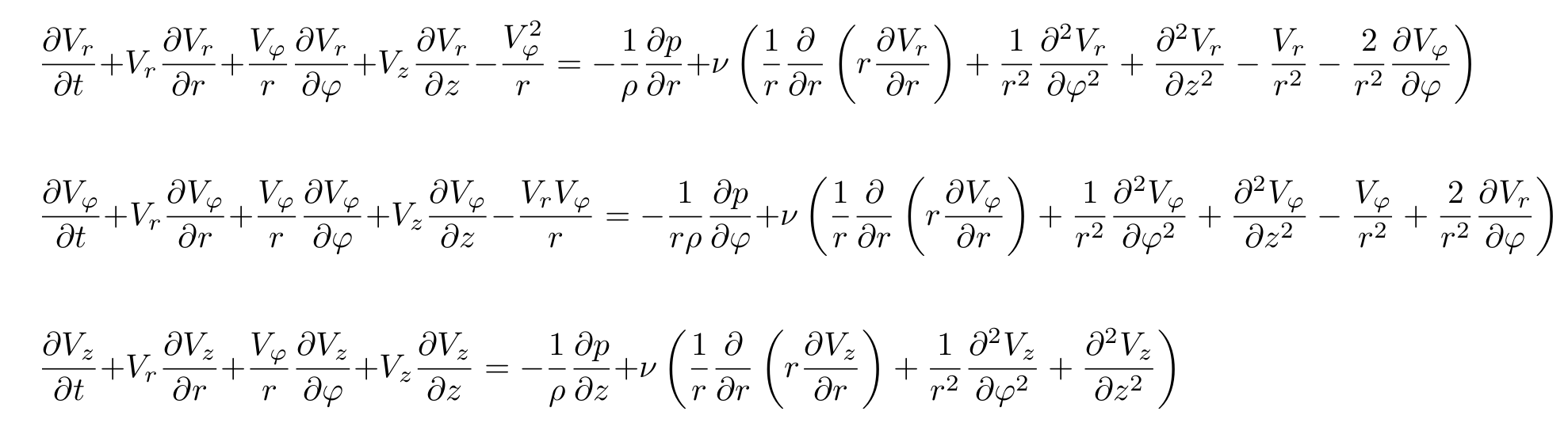
Ici ro est la densité du liquide, et nu est la viscosité cinématique.
Il est très difficile de résoudre un tel système d'équations sous une forme analytique, nous allons donc faire deux simplifications raisonnables. Tout d'abord, nous supposerons que le fond du verre n'affecte pas la forme du liquide, c'est-à-dire le verre est assez profond. Deuxièmement, nous supposerons que la vitesse de rotation du liquide dans un cercle est beaucoup plus grande que la vitesse de déplacement du liquide de haut en bas et du centre du verre vers et depuis ses parois. Ceux. ces vitesses peuvent être négligées. Compte tenu de ces simplifications, la troisième équation de notre système se transformera en identité, et les deux autres ressembleront à ceci :
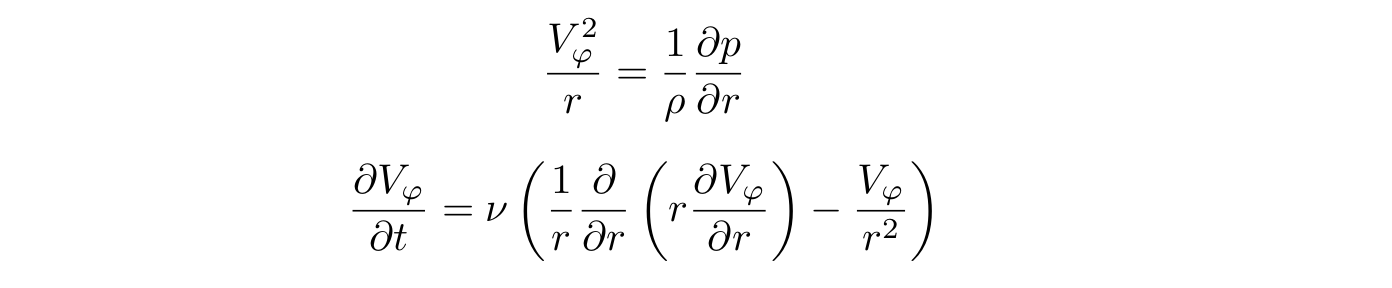
La pression à l'intérieur du liquide en tout point est directement proportionnelle à la colonne de liquide au-dessus de ce point et est calculée à l'aide de la formule bien connue :
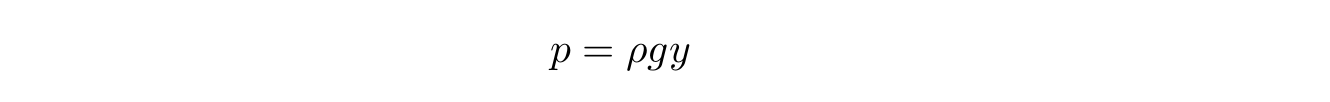
g - , y - z, , , . , :
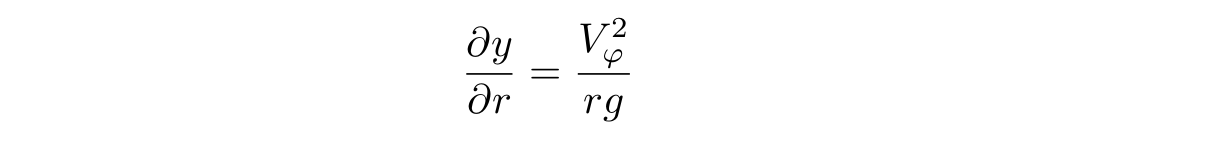
, omega , , :
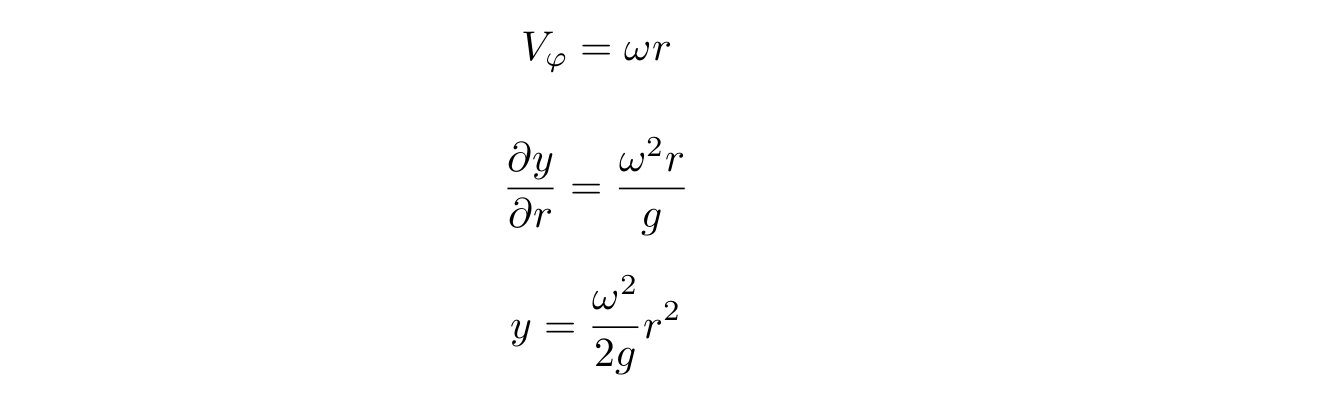
, , , , . :

, , , . , , , , :
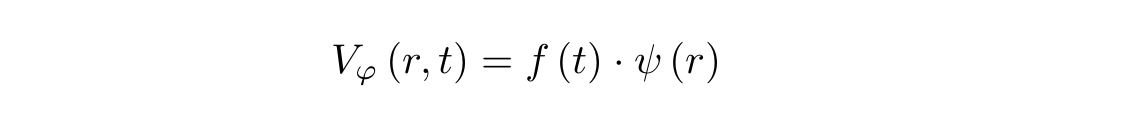
, :
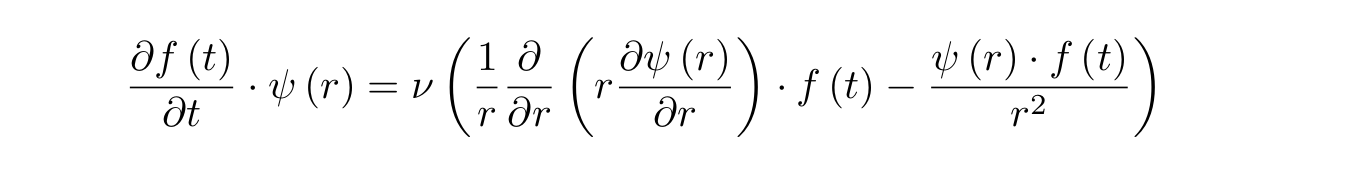
, , ,
r. , :

, r:

:
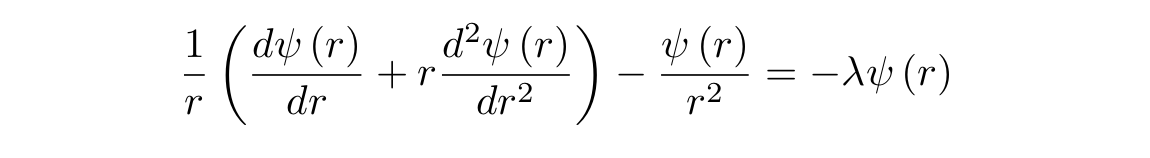
:
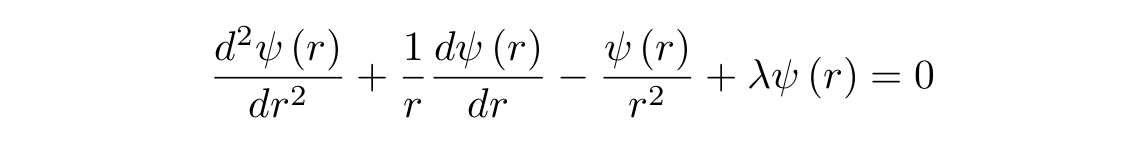
r :
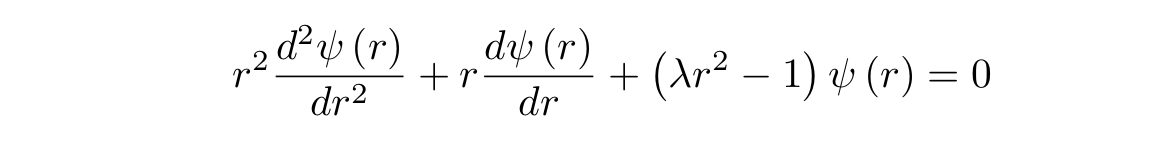
, . , :
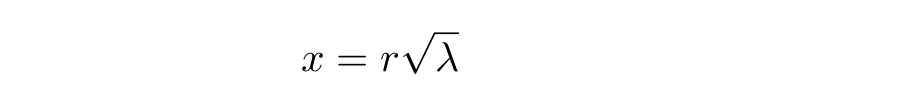
:
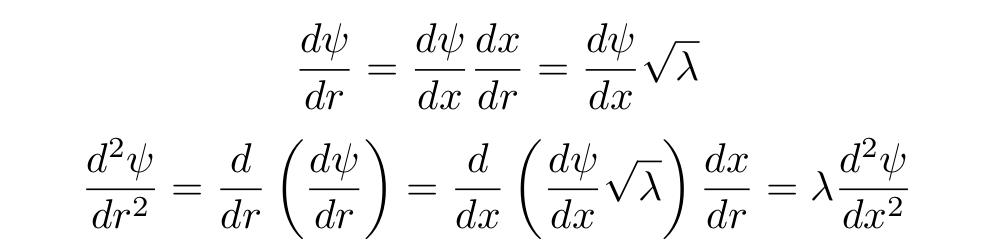
:
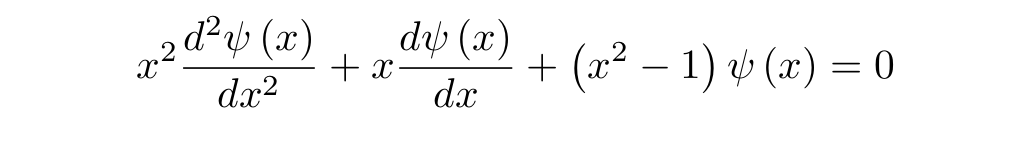
. , , , , , :

.

R - ,
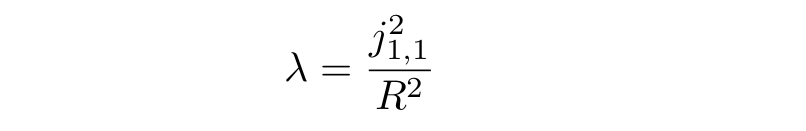
, :
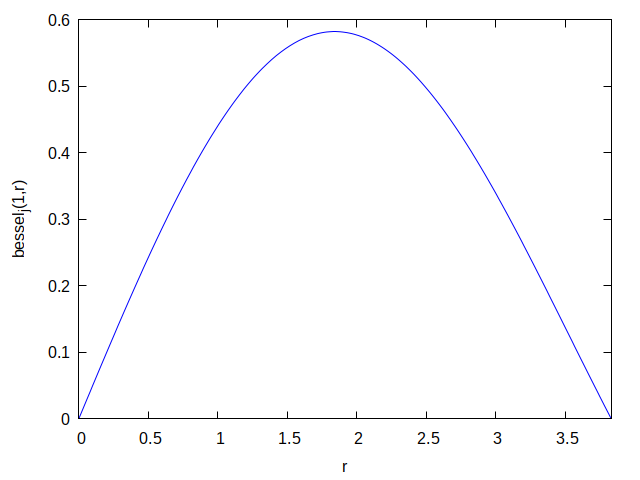
, , , :
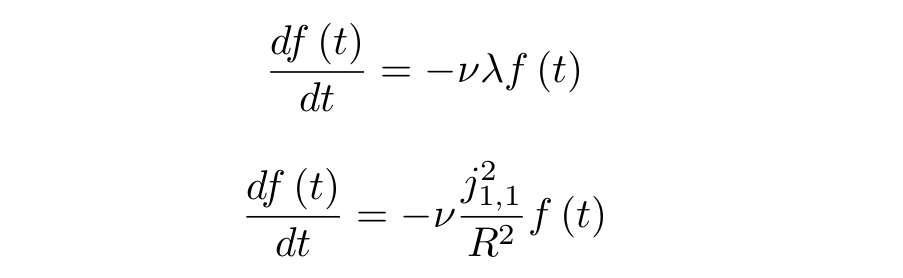
, :
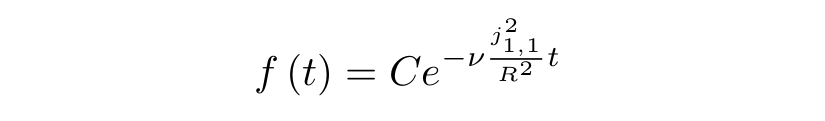
C - . , :
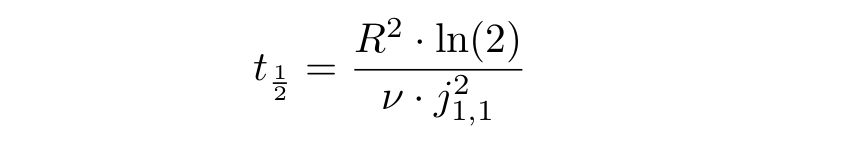
:
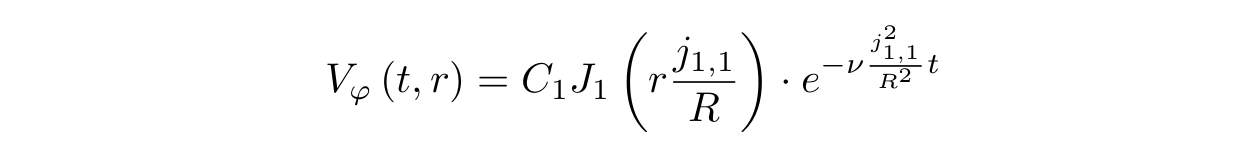
Trouvons maintenant, en effet, la forme de la surface. Pour ce faire, nous substituons la valeur de la vitesse tangentielle dans l'équation pour y :
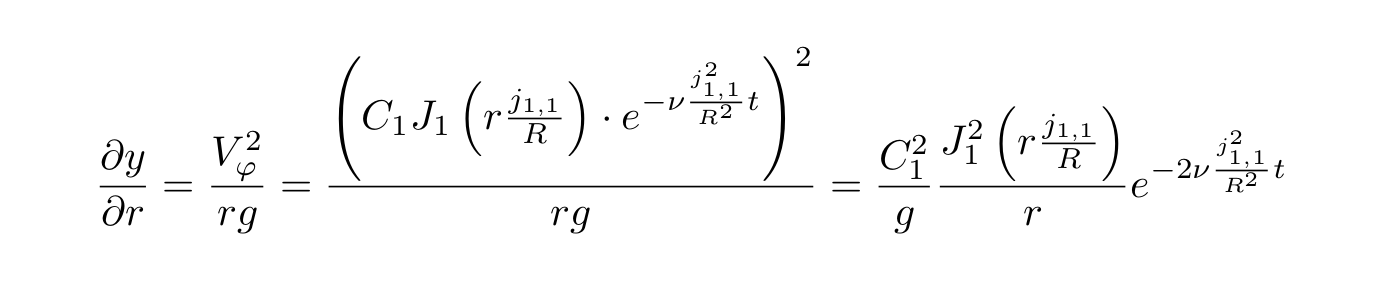
Nous intégrons et obtenons :

Ici, C1 et C2 sont des constantes qui dépendent de la vitesse de rotation du liquide et de la profondeur de notre verre. Notre profil de fluide rotatif ressemblera à ceci :
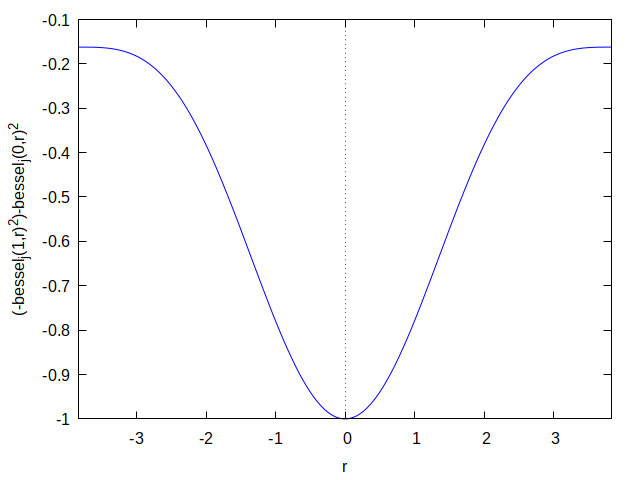
Et si vous le représentez en 3D, alors comme ceci :

Si cela ressemble à la vraie forme de thé que vous avez le matin, écrivez dans les commentaires.