😙 👉🏽 😊 Comment se forment les trous de ver astrophysiques et comment nous pouvons les observer 👃🏿 👩🏽‍🤝‍👨🏾 🧗🏿

Vous pouvez écrire n'importe quelle question ou commentaire dans les commentaires. Je suis également ouvert à un dialogue personnel dans un télégramme ou à une conversation dans notre chat . J'ai aussi une chaîne de télégrammes sur la cosmologie.

introduction

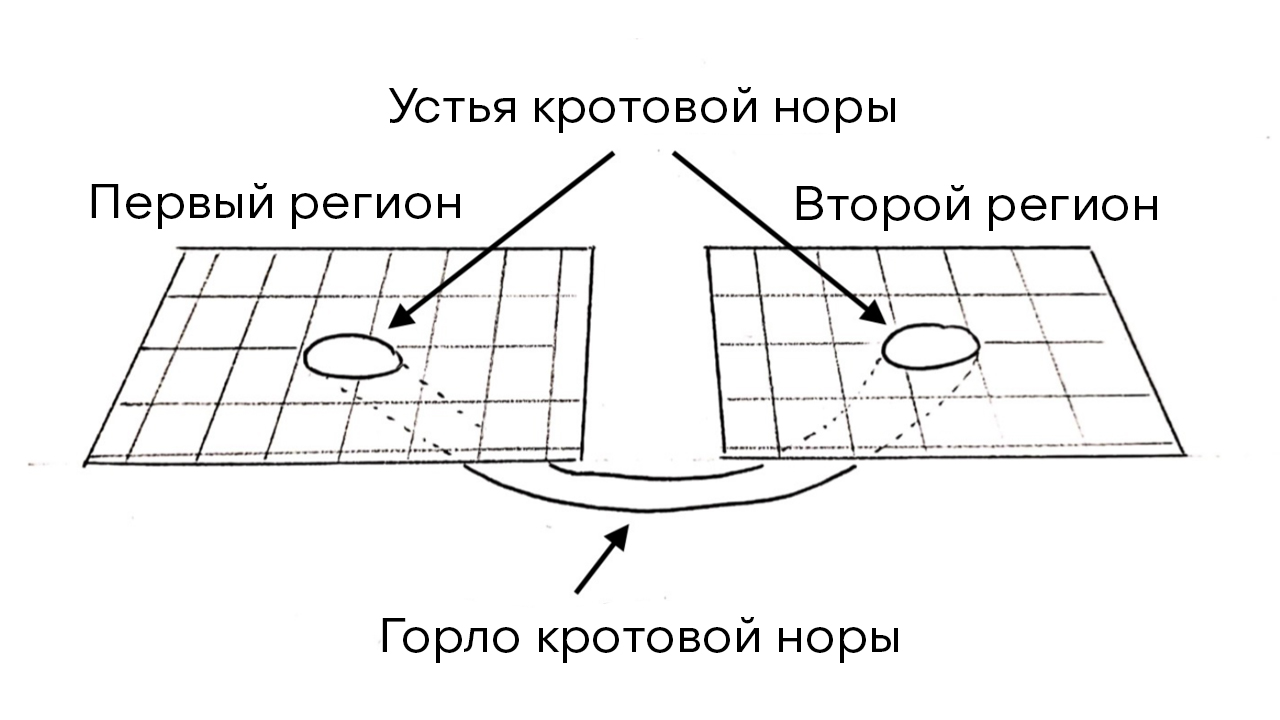
Wormholes, wormhole ou wormholes (Angl.: Wormholes ) - cette structure spatio-temporelle hypothétique avec une topologie non triviale (voir note 1.) Reliant une ou deux zones de l'univers, ou deux univers différents (voir Figure 1..). Les entrées du trou de ver sont appelées "bouches", et la zone entre les "bouches" ( bouche ) appelée "gorge" ( gorge ). La configuration la plus simple d'un trou de ver est deux bouches reliées par une gorge. Des structures plus complexes de taupinières sont également possibles [1].

Note du traducteur 1 : Une topologie triviale est une topologie qui a le nombre minimum possible d'ensembles ouverts, c'est-à-dire ensemble vide et tout l'espace. Si nous supposons qu'il existe deux univers différents avec la topologie d'une sphère et connectés l'un à l'autre par un seul trou de ver, alors un tel espace-temps aura la topologie triviale d'une sphère. Si, cependant, deux parties différentes du même univers sont reliées par un trou de ver, alors un tel espace-temps aura déjà une topologie de tore non triviale. Si deux univers avec une topologie de sphère sont connectés par deux ou plusieurs trous de ver, alors l'espace-temps résultant aura également une topologie non triviale. Un système d'univers reliés par plusieurs trous de ver,aura également une topologie non triviale.

Fig. 1 : Si nous imaginons notre espace tridimensionnel comme une surface bidimensionnelle, alors un trou de ver peut être représenté comme une surface cylindrique reliant deux régions du même univers ou deux univers différents. Les entrées du trou de ver sont appelées ses bouches, elles sont reliées par la gorge. — .1: , , . , .

, .. , , , - , . - — .

(. "..."), [2], 1957 [3]. "" "" — , , .. , . , — [6-8], , . [11-14].

, , . , , , , .

. , , .

, , . (. 2). .

2: , , , - , , .

, -

$\delta s^2 = -\left(1-\frac{2GM}{r}\right)\delta t^2 + \frac{\delta r^2}{1-\frac{2GM}{r}} + r^2 \delta \Omega.$

, . , (. . 2). , , , . , , , . , . , , , . , .

.2: -. (), (. 3). : ( .: null infinity).

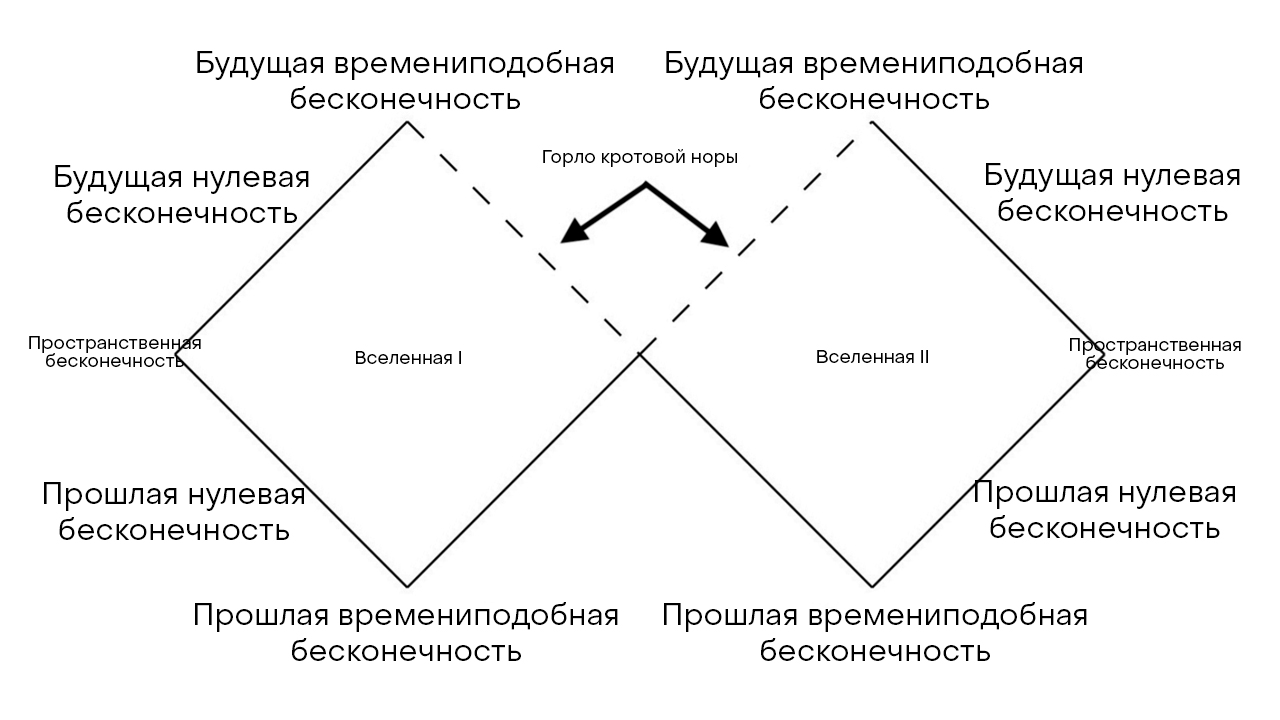
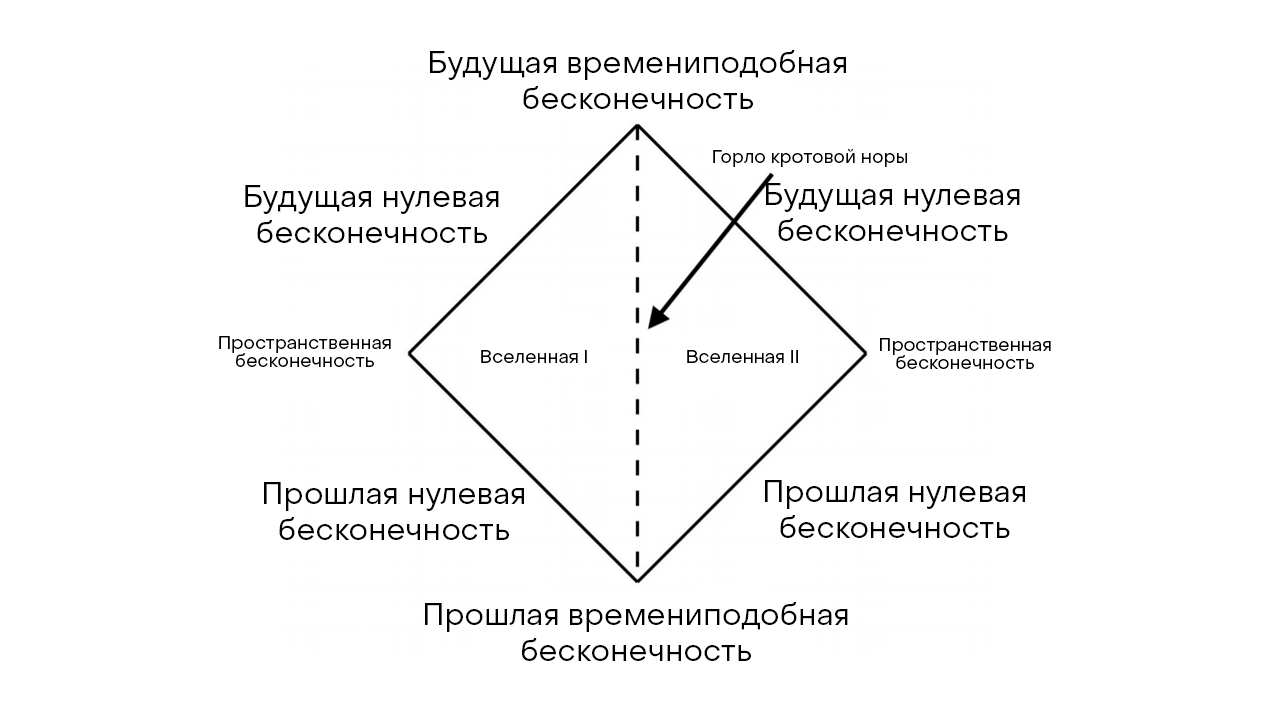
3: - . , , , , . — , , , ( ), , , ( ). (time-like), (null) (spatial), , .

, - . , , . , . , .

, 3+1- [27-29]. : , , , . , , , , - , . , , , , , .

, , , . , : , , , . (.: ).

.

, . [33, 34]. , -; [35].

.

, , , . ( ) .

, ( ), — (.: «perturber»). - R , , .. R > rg ≡ 2GM. perturber' -:

$a \approx -\mu \frac{R}{A}\frac{1}{r^2},$

µ — -, A — , r — . :

$\Delta a = \mu R\left(\frac{1}{r_p}-\frac{1}{r_a}\right)\frac{1}{r^2}.$

, r_a> r_p, :

$\Delta a = \mu \frac{R}{r_p}\frac{1}{r^2}.$

— S2, Sgr A*, M = 4 × 10⁶ M. S2 14M, 15,9 1031,69 . 1,5 /² 4 × 10^-4 /². , , ( , Sgr A* ) S2 . , .

.6: µ ( , M) rp ( , 2GM) , Sgr A* S2 . S2, 4×10^−4 /*, 2×10^−5 /* 10^−6 /* .

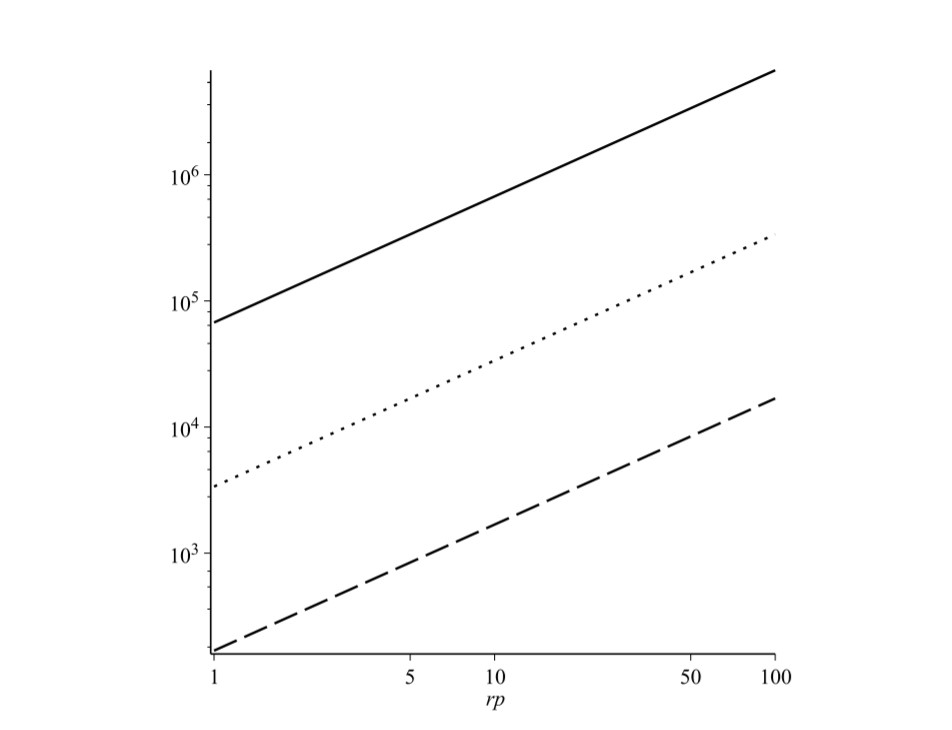
— . , , [62]. , , , T₀. . , :

$\mu > \frac{1}{G}\frac{r'_p}{r_g} r^2_{avg} \frac{1}{f'^2 T'} \sigma_{\nu} \left (\frac{T'}{\tau}\right)^{1/2},$

r_avg — ( ), f₀ = r'_p/r'_a, σ_v — . , T₀ ∝ r'_p^3/2 ∝ r'_p^1/4.

, «» , - . , R = 10⁶ ∼ 106 r_g ∼ 4 , S2 .

.

.. «» 20 [71]. - [72]. M87, Event Horizon Telescope Collaboration [16].

. - , . [73] , , - (. . 7). , , , , , .

, , , . . , ( ) [83]: - .

— , [84, 85]. . , , .

.

, . , .. , .

. 7. , . . (M ∼ 10 M) (0,1-1 ), (M ∼ 10⁵-10¹⁰ M) — (1-100 ). .. «», (T_e ∼ 100 ) . , [90].

Fig. 8 : Un objet compact avec un disque d'accrétion géométriquement mince et optiquement épais. L'illustration est tirée de [89]. — .8: . [89].

[91-94]. , . -, , .. - . -, , , [95].

, , , , , , - [103].

.

- . , - , - , , .

Figure 9 : Evolution de la déformation, de la séparation d'un trou noir et de sa vitesse relative pour l'événement GW150914 au cours du temps. L'illustration est tirée de [15]. — .9: , GW150914 . [15].

LIGO Virgo , . : , . , . , . . , , .

, , -. , , , [104], 5M 200M. , , , , , - ( eLISA). [105]. , - .

(KHM), [107-113]. - , KHM, .

— , . , . , . , , .

2105.00881 (gr-qc) arXiv.org 3 2021 , 8 2021 . astro-ph . : « . , , , , , . , - ». , , .

Bon, je vous rappelle aussi que le lecteur n'hésite pas à me poser une question ou à me corriger dans les commentaires. J'ai aussi une chaîne de télégrammes où je parle des dernières nouvelles en cosmologie et astrophysique, et j'écris aussi sur l'astrophotographie. Écrivez-moi dans un message personnel ou sur notre chat . Tout bon!

Comment se forment les trous de ver astrophysiques et comment nous pouvons les observer

introduction

, -

.

.

.

.

.

More articles: