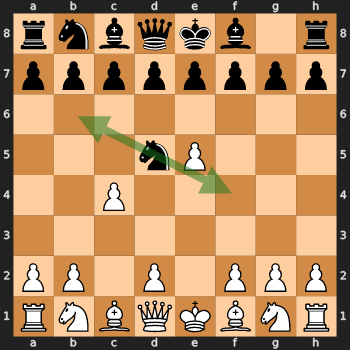
C'est l'histoire de la façon dont j'ai essayé de gagner une partie d'échecs avec mon frère. Juste un putain de jeu. Qu'est-ce qu'il a de si spécial ? Suis-je bon aux échecs ? Pas du tout. Ai-je appris quelque chose en jouant ? Aussi non. C'est peut-être l'histoire d'un voyage pour un voyage, pas un but ? Pas vraiment. Est-ce que j'ai même apprécié? Pas certain.
C'est l'histoire de ma tentative d'être original dans l'un des jeux les plus étudiés au monde, en utilisant une expérience de développement de logiciels là où cela n'est peut-être pas nécessaire.
Malgré ma stupidité absolue aux échecs et l'inutilité totale de cet article pour ceux qui cherchent à améliorer leur jeu, je pense toujours qu'il valait la peine de partager une manière originale d'appliquer les principes d'ingénierie à un problème. Est-ce que je réussis ? Vous apprendrez à ce sujet à la fin.
Pourquoi je me suis même impliqué dans les échecs
Pendant la pandémie de 2020, mon frère, comme beaucoup d'autres personnes, est devenu accro aux échecs en ligne. Après avoir joué pendant quelques mois, il a commencé à parler de ce jeu de manière très inspirée et à défier les autres membres de la famille. Notre père a répondu à l'appel (bien qu'il ait subi un fiasco numérique), mais je n'ai pas cédé. L'un des facteurs limitants était ma réticence à plonger dans un passe-temps potentiellement très chronophage. J'en savais assez sur ce jeu pour me rendre compte que devenir même un joueur intermédiaire nécessite de passer des centaines voire des milliers d'heures à y jouer. Même si j'avoue qu'en même temps je n'étais pas non plus inspiré par l'idée de perdre contre mon frère, qui à l'époque avait déjà joué plus d'une centaine de matchs. Je n'en suis pas un.
Pourtant, un jour, j'ai succombé à son défi. Inutile de dire que la perte a été dévastatrice. Je connaissais les règles et les bases du jeu, puisque j'ai joué un peu quand j'étais enfant, mais cela ne pouvait en aucun cas être comparé aux compétences de mon frère. Plus tard, en regardant l'analyse du jeu sur chess.com , j'ai vu que mon décalage tactique ne faisait qu'augmenter , coup par coup, jusqu'à atteindre la marque de +9 (ce qui équivaut à perdre une tour, un fou et un pion contre l'absence des pertes ennemies). A ce moment-là, ayant perdu tout espoir, j'ai abandonné. Une situation similaire s'est répétée pour quelques jeux supplémentaires, lorsque j'ai réalisé qu'il fallait faire quelque chose à ce sujet.
Ma première décision a été d'approfondir le jeu.
Première tentative : étudier
Ma première tentative pour améliorer la qualité du jeu était une évidence : allez sur Reddit et YouTube pour obtenir des recommandations d'autres étudiants. Entre les leçons de GM Naroditsky , la lecture et la résolution de problèmes sur Lichess, j'ai également joué à quelques jeux avec des adversaires aléatoires sur Internet. Malgré tout cela, ma note est restée faible (1300 - 1400 Rapid sur Lichess).

Après quelques matchs de plus contre mon frère, je me suis rendu compte que je n'avais aucune chance de gagner. J'ai continué à suivre toutes les mêmes méthodes de développement (jouer, étudier des techniques et regarder des vidéos), mais j'y ai consacré beaucoup moins de temps que mon frère. A cette époque, il jouait déjà des centaines de matchs par mois, alors que je n'avais pas plus de 10 ans. A ce rythme, mon écart grandissait de plus en plus.
C'est alors que j'ai réalisé une nuance très importante : je n'étais pas particulièrement intéressé par le jeu lui-même, et, en fait, je ne voulais pas m'améliorer. L'objectif principal pour moi était de vaincre une seule personne - mon frère.
Deuxième tentative : étudier l'ennemi
Une partie d'échecs est généralement divisée en trois phases : l' ouverture , le milieu de partie et la fin de partie . Après avoir appris quelques schémas d'accouplement de base, il est généralement "facile" de passer d'un gros avantage à une victoire en phase finale, donc obtenir cet avantage était la première question pour moi.
Au stade intermédiaire, l'avantage est généralement obtenu en déployant une stratégie à long terme et en appliquant des tactiques . La stratégie peut être améliorée en lisant et en étudiant les principes du jeu (j'aime ça), et les tactiques ne se développent qu'en résolvant des problèmes(que je déteste particulièrement). Par conséquent, j'ai compris que dans les compétences tactiques, j'aurais définitivement du retard, étant donné que mon frère résolvait environ 20 de ces problèmes sur chess.com chaque jour. Pour moi, c'était une limite inaccessible. Ainsi, il ne restait qu'une seule opportunité : prendre l'avantage lors de la phase d'ouverture.
La théorie derrière la phase d'ouverture est énorme. En même temps, cela nécessite de mémoriser de longues séquences et variations de coups, ainsi que les réponses possibles de l'adversaire. Les débutants n'ont pas besoin de beaucoup mémoriser, mais une certaine familiarité avec les ouvertures les plus typiques peut être très utile (du moins c'est ce qu'on me dit).
Ensuite, j'ai décidé de regarder certains des jeux aléatoires de mon frère et d'essayer de comprendre les ouvertures qu'il utilisait. J'ai aussi étudié les débuts de Lichess "Parti italien" et la Défense sicilienne , essayant de se rappeler leurs principes de base. En dehors de cela, j'ai regardé un tas de vidéos YouTube.
Évidemment, mon frère a fait tout ça avant moi (et mieux), alors naturellement j'ai encore perdu. Sans parler du fait que mémoriser des mouvements d'ouverture dénués de sens (du moins pour moi) n'est qu'ennuyeux et fatigant. Tout cela ne me faisait aucun plaisir. Un autre problème était que lorsque mon adversaire a commencé à s'écarter des mouvements prescrits dans le livre, je ne savais absolument pas comment réagir, car je ne comprenais tout simplement pas les positions émergentes.
Il est temps de prendre du recul et de réfléchir à nouveau. Puis j'ai réalisé que j'essayais en fait de ne pas battre mon frère, mais d'améliorer mon jeu contre des adversaires qui jouaient parfaitement les mêmes ouvertures. Aurais-je pu agir de manière plus directionnelle ? Aurait-il pu plutôt se préparer spécifiquement contre les faiblesses de son frère ? Évidemment, cette approche ne fonctionnerait que contre lui, mais c'était tout à fait conforme à mon objectif.
Troisième tentative : programmation
Maintenant ma tâche a pris une autre forme : trouver des positions à la sortie de l'ouverture, que mon frère (ci-après PlayerX) est le plus susceptible d'atteindre, tout en étant désavantagé. Veuillez noter qu'aucun de nous n'est expert dans le jeu, et que les joueurs de notre niveau ne jouent pas très prudemment.
La seule façon de contrer un bon joueur est de suivre exactement les mouvements du livre, car alors vous savez au moins que votre adversaire ne fera aucun mouvement, gagnant ainsi un avantage. Cependant, la situation change lorsque vous jouez contre un joueur de niveau club. Vous pouvez prendre des risques (c'est-à-dire vous retrouver temporairement dans une situation désavantageuse) si vous savez qu'il est peu probable que l'ennemi puisse réagir correctement à cela et qu'il se trouve donc dans une position difficile.
J'avais aussi une liste de plus de 500 jeux auxquels mon frère jouait sur chess.com. Et puisque je suis programmeur, il est devenu naturel pour moi de résoudre ce problème de manière technique.
J'ai commencé à télécharger les jeux auxquels il jouait en utilisant l'API chess.com et à les diviser en jeux blancs et noirs. Ensuite, je me suis concentré sur les jeux où mon frère jouait pour les noirs, car je sentais que j'avais une meilleure chance de diriger le jeu dans la direction que je voulais en jouant pour les blancs.
import json
import requests
def get_month_games(player, yyyy_mm):
url = 'https://api.chess.com/pub/player/{}/games/{}'
r = requests.get(url.format(player, yyyy_mm))
if not r.ok:
raise Exception('get_month_games failed')
games = json.loads(r.content)
# Format: {games: [{url, pgn}, ...]}
return games['games']
# ...
import chess.pgn
import io
import json
with open('games.json') as f:
data = json.load(f)
games = []
for game in data:
pgn = io.StringIO(game)
games.append(chess.pgn.read_game(pgn))
black_games = [g for g in games if g.headers["Black"] == "playerx"]
Puis j'ai formulé la tâche comme suit : « Compte tenu de toutes les positions que PlayerX a vues, laquelle d'entre elles sera probablement la moins rentable pour lui à la fin de l'ouverture ?
Cette fois, la tâche était clairement définie et le travail a commencé dans un domaine qui m'est familier. J'ai décidé de faire l'analyse en Python, notamment dans le notebook Jupyter , car je n'avais pas pour objectif de créer un outil réutilisable, et je n'avais qu'à étudier les données disponibles pour trouver une solution.
Il s'est avéré que Python possède déjà d'excellentes bibliothèques pour travailler avec les échecs : python-chess (génération de mouvements, évaluation et visualisation) et python stockfish(fixations pour évaluer une position aux échecs à l'aide du célèbre moteur d'échecs Stockfish).
J'ai converti le problème en graphique de cette manière : un nœud est une position particulière aux échecs (décrite dans la notation FEN ). Une arête relie deux nœuds, tandis que la position cible est accessible depuis la position initiale par un mouvement admissible. Tous les jeux ont un seul et même nœud de départ : la position de départ.
Ensuite, j'ai construit un graphique de tous les jeux joués par PlayerX en tant que Black, en marquant en plus chaque bord avec le nombre de fois que le mouvement correspondant a été effectué.
class GamesGraph():
def __init__(self):
self.graph = igraph.Graph(directed=True)
def add_move(self, start_fen, end_fen, uci):
vs = self._ensure_vertex(start_fen)
vt = self._ensure_vertex(end_fen)
try:
e = self.graph.es.find(_source=vs.index, _target=vt.index)
e["count"] += 1
except:
e = self.graph.add_edge(vs, vt)
e["uci"] = uci
e["count"] = 1
@property
def start_node(self):
return self.graph.vs.find(chess.STARTING_FEN)
def _ensure_vertex(self, fen):
try:
return self.graph.vs.find(fen)
except:
v = self.graph.add_vertex(name=fen)
v["fen"] = fen
v["turn"] = chess.Board(fen).turn
return v
En conséquence, nous avons obtenu un graphe orienté pondéré (pas un arbre, car une position peut être obtenue par une séquence de mouvements différente) comme celui-ci (synthétique, car un vrai ne conviendrait tout simplement pas ici):

Ici la position de départ est indiquée par un nœud carré, la couleur indique s'il est blanc ou noir pour se déplacer dans cette position.
Je voulais également obtenir une évaluation de chaque position en termes d'avantage blanc, pour laquelle j'ai utilisé Stockfish. Étant donné que le processus d'évaluation de milliers de positions prend du temps, j'ai décidé de l'exécuter séparément et j'ai créé un objet JSON mappant chaque position FEN unique à son estimation Stockfish.
from stockfish import Stockfish
stock = Stockfish(parameters={"Threads": 8})
stock.set_depth(20)
stock.set_skill_level(20)
def eval_pos(fen):
stock.set_fen_position(fen)
return stock.get_evaluation()
# fens - FEN .
for fen, node in graph.fens.items():
node.eva = eval_pos(fen)
L'évaluation de l'avantage était renvoyée en centipoints ou en « échec et mat en X coups », où un nombre positif signifie un avantage pour les blancs et un avantage négatif pour les noirs :
{"type":"cp", "value":12} # 12 .
{"type":"mate", "value":-3} # .
100 centipoints signifient un avantage sur l'adversaire d'un pion, et 300 signifie une pièce mineure comme un fou. Cependant, il est à noter que Stockfish attribue une valeur aux pièces en fonction de leur position, ce qui signifie qu'il est tout à fait possible d'avoir un avantage de 1000 centipoints même avec un nombre égal de pièces sur l'échiquier.
J'avais besoin de mapper ce score en quelque chose de plus pratique pour le traitement, par exemple, des nombres entre 0 et 1. Pour cela, j'ai décidé d'emblée qu'un avantage de 300+ serait affiché en 1.0 et un décalage de 300+ en 0. De plus, n'importe quel mat en X coups (même si X vaut 20) sera 1 ou 0.
# [-1;1]
def rating(ev, fen):
val = ev["value"]
if ev["type"] == "cp":
# -300, +300. .
val = max(-300, min(300, val))
return val / 300.0
# X : max .
if val > 0: return 1.0
if val < 0: return -1.0
# , ?
b = chess.Board(fen)
return 1.0 if b.turn == chess.WHITE else -1.0
# [0;1], 0 - min, 1 - max .
def rating_black(ev, fen):
return -rating(ev, fen) * 0.5 + 0.5
Maintenant, toutes les informations étaient hors de propos, et je devais trouver les nœuds du graphique (c'est-à-dire les positions), dans lesquels Noir était en position perdante, ainsi que la séquence de mouvements la plus appropriée pour les atteindre. Il était nécessaire de peser les côtes de manière à pouvoir calculer facilement la probabilité d'atteindre une position particulière. J'ai raisonné ainsi :
- Dans chaque position, vous pouvez estimer la probabilité de faire un mouvement particulier en divisant le nombre de passes le long du bord correspondant par le nombre total de mouvements effectués à partir de cette position.
- Chaque bord aura désormais un poids compris entre 0 et 1, où une valeur plus élevée reflète une probabilité plus élevée de le traverser à partir de cette position.
- Alors la probabilité de passer un chemin particulier sera le produit des probabilités de toutes les arêtes traversées.
Pour résoudre le problème à l'aide d'algorithmes de graphes standard, il a été nécessaire de transformer les poids des bords de sorte que :
- Ils représentaient la distance et non la probabilité (c'est-à-dire que plus la distance est grande, plus la probabilité de choisir un chemin est faible).
- La distance entre deux nœuds était la somme des poids des arêtes traversées (par opposition au produit des probabilités).
En fait, c'est beaucoup plus facile à faire qu'à expliquer. La formule est très simple :
distance(e) = -log(prob(e))
En Python, cela ressemblerait à ceci :
def compute_edges_weight(vertex):
all_count = sum(map(lambda x: x["count"], vertex.out_edges()))
for edge in vertex.out_edges():
prob = edge["count"] / all_count
edge["prob"] = prob
edge["weight"] = -math.log(prob)
Prendre le logarithme de la probabilité de choisir une arête donnera un nombre négatif, car la probabilité est comprise entre 0 et 1. Il n'y a pas lieu de s'inquiéter du cas où la probabilité est nulle (à la suite de quoi le logarithme donnerait moins l'infini), puisque chaque arête du graphe a été parcourue au moins une fois... Plus la probabilité est faible, plus le logarithme sera négatif, ce qui signifie que l'inversion de son signe donnera ce dont nous avons besoin, car :
- La somme des logarithmes est le logarithme du produit de leurs arguments
log(a) + log(b) = log(a*b)
. - Plus le résultat est élevé, plus la probabilité qui le détermine est faible.
Armé de cette idée, vous pouvez calculer le chemin le plus court entre le nœud de départ et tous les autres nœuds en utilisant l'algorithme de Dijkstra . Le résultat est un mappage entre chaque nœud et le chemin le plus court vers la position de départ, représentant la séquence de mouvements la plus probable qui y mène.
À ce stade, j'ai choisi arbitrairement la valeur minimale de l'avantage et j'ai ordonné les chemins par probabilité. Les premiers chemins représentaient la plus grande chance pour moi de sortir de mes débuts avec un avantage sur PlayerX.
Améliorations
Qu'ai-je découvert ? Parmi les positions données par cet algorithme figurait la suivante (mouvement des Blancs) :
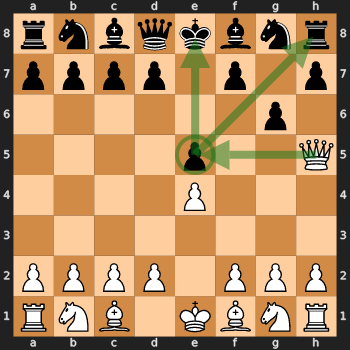
Comme vous pouvez le voir, Noir est dans une position très délicate (+8,9 selon Stockfish) car g6, le dernier coup de Noir, était une erreur. Les blancs continuent, prenant le pion de e5 et la tour. A ce stade, la partie pour les Noirs est pratiquement terminée, puisqu'il devra sauver le cavalier, le pion en h7 et le fou. Un autre résultat de l'algorithme était le suivant (mouvement des blancs) :

Ici, nous voyons un échec et mat en un seul mouvement ( échec et mat des enfants ).
Le problème est que PlayerX n'a commis ces erreurs que quelques fois lors de ses premiers jeux et ne les a plus répétés. Les premières attaques de reines ne sont généralement effectuées que par des joueurs inexpérimentés et ne sont efficaces que contre des joueurs du même niveau. Ayant quitté la catégorie des débutants, PlayerX n'a pas fait ces erreurs depuis longtemps, car des adversaires plus compétents ne vont pas dans ce sens. Je savais qu'une telle ouverture ne fonctionnerait pas, car PlayerX savait comment s'en défendre.
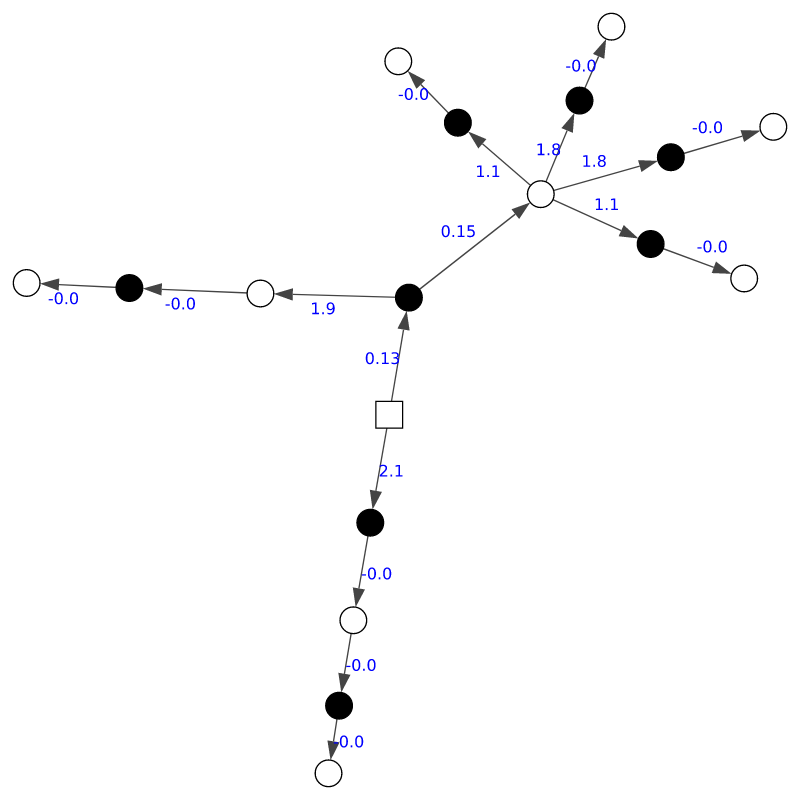
Un autre problème était lié aux séquences de mouvements, qui ne se produisaient qu'une seule fois, mais à partir de positions typiques. La probabilité de leur position finale s'est avérée être la même que la probabilité de la dernière position typique, car chaque arête avait une probabilité de 1,0 (étant donné qu'aucune autre possibilité n'a été jouée). Dans l'exemple ci-dessous, vous pouvez suivre les arêtes 7 et 6 (la position la plus courante au deuxième coup), puis l'une des arêtes avec des 1. De plus, tous les coups suivants ne seront joués qu'une seule fois (car cette position n'a été formée qu'en un seul match), ce qui fait que chaque coup aura une probabilité de 1,0.

Et voici les probabilités :

On ne peut pas faire confiance à un tel schéma, car il est peu probable que la même séquence de coups soit jouée sans ambiguïté. Pour une telle conclusion, nous n'avons pas assez de jeux dans lesquels le jeu se déroulerait à partir de ces positions.
La célèbre citation ( B. Brewster ?) : "En théorie, il n'y a pas de différence entre la théorie et la pratique, mais en pratique il y en a" s'est avérée correcte dans ce cas, j'avais donc besoin de quelques améliorations et recherches indépendantes pour trouver des hypothèses plus réussies postes.
J'ai résolu le deuxième problème en fixant une limite supérieure sur la probabilité d'un bord de sorte que de longues séquences de coups jouées une seule fois perdraient progressivement leur probabilité.
def compute_edges_weight(vertex, prob_ceiling=0.9):
all_count = sum(map(lambda x: x["count"], vertex.out_edges()))
for edge in vertex.out_edges():
# ... (default 90%).
prob = min(edge["count"] / all_count, prob_ceiling)
edge["prob"] = prob
edge["weight"] = -math.log(prob)
Pour le premier problème, j'ai juste filtré manuellement les mauvaises hypothèses. En conséquence, il ne me restait plus que quelques postes à travailler.
La raison d'une autre modification était que je ne voulais pas que les probabilités des mouvements des Blancs influencent la probabilité de choisir un chemin, car je jouais pour les Blancs et pouvais décider moi-même quel chemin prendre. Pour cette raison, j'ai défini toutes les probabilités des mouvements de Blanc à 1,0 (poids nul), ce qui donne un graphique comme celui-ci :

Préparation
En cours d'étude, j'ai choisi le poste suivant :

Selon Lichess, il s'agit de la Défense Alekhine (attaque de deux pions). Dans cette position, Noir n'a qu'un coup réussi (Nb6), après quoi il reste toujours dans une position moins avantageuse (+0,6 selon Stockfish). Cependant, à partir de cette position, PlayerX joue souvent Nf4, ce qui est très regrettable pour lui (+2,3). J'ai monté un studio sur Lichess et j'ai commencé à étudier quelques variantes (bons coups et coups joués par PlayerX).
En fin de compte, j'ai eu un arbre des possibilités, que j'ai essayé de me rappeler et de comprendre. Par exemple, je devais découvrir ce qui menaçait un coup comme d5, pourquoi Nf4 n'avait pas réussi et préparer des réponses optimales pour tous.
Je ne l'ai pas fait longtemps, car je me suis vite ennuyé, et en fait je n'étais que partiellement préparé.
Jeu décisif
Tout s'est passé comme si je regardais vers l'avenir : PlayerX et moi étions dans la position de défense d'Alekhine. Se retrouvant dans une situation inconfortable, il manqua son cavalier au cinquième coup. Il s'avère que même des joueurs beaucoup plus expérimentés que vous commencent à faire des erreurs les uns après les autres lorsqu'ils se retrouvent dans des conditions perdantes. Il est facile de jouer clairement quand vous gagnez, mais pouvez-vous garder votre sang-froid dans la situation inverse ? Au 10ème coup, j'étais déjà en tête avec un avantage de +7.1, ce qui rend difficile la défaite, mais c'était aussi la fin du schéma que j'avais élaboré. Jetez un œil à l'étroitesse des noirs maintenant et à la façon dont mes pièces visent à attaquer le roi :

A partir de ce moment-là, j'ai commencé à faire des erreurs ici et là, mais en même temps j'ai réussi à conserver un certain avantage jusqu'au coup 27 :
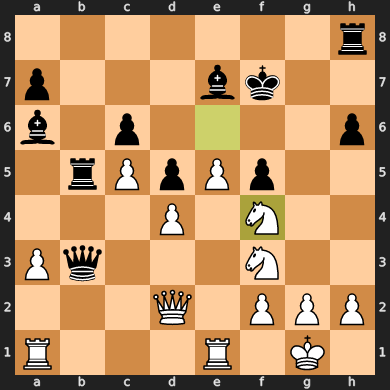
Malheureusement, j'avais un temps très limité (nous avons joué un jeu accéléré de 10 minutes), donc j'ai dû marcher vite. Au final, j'ai fait des erreurs fatales sur 32 et 33 coups, et après un de plus j'ai reçu un échec et mat de mon adversaire invaincu : /

Voici le match complet (avec des erreurs grossières et ainsi de suite):

Aperçu du lot en direct : lichess.org/2qKKl2MI
conclusions
Qu'ai-je appris de tout cela ? Quelques éléments, dont la plupart semblent évidents rétrospectivement :
- Se préparer pour un adversaire spécifique peut vous donner un avantage d'ouverture significatif.
- Les joueurs novices manquent souvent l'occasion de profiter des mouvements douteux de l'adversaire. À cet égard, il est facile de prendre l'avantage en poussant l'ennemi vers une position à partir de laquelle il n'y a qu'un seul coup d'État.
- . , . .
- , , . .
- , , .
Le code que j'ai utilisé est dans le dépôt. Notez que je n'y ai pas inclus les données et que le code lui-même est assez bâclé. Néanmoins, j'espère qu'il sera utile, surtout pour ceux qui songent encore à maîtriser l'informatique. Regardez - il est tout à fait possible avec son aide de résoudre des problèmes dans la vie réelle, il ne s'agit donc pas seulement de déplacer des bits d'avant en arrière.
C'est tout, les amis. J'espère qu'un jour je pourrai vaincre mon frère, mais pour l'instant je vais essayer d'y parvenir... par mes propres moyens.

