FAISS: trouvez rapidement des visages et des clones sur des données de plusieurs millions de dollars

Une fois, à la veille d'une conférence clients organisée chaque année par le groupe DAN, nous avons réfléchi à la possibilité de penser à des choses intéressantes pour que nos partenaires et clients aient des impressions et des souvenirs agréables de l'événement. Nous avons décidé d'analyser une archive de milliers de photos de cette conférence et de plusieurs précédentes (et il y en avait 18 à ce moment-là): une personne nous envoie sa photo, et en quelques secondes nous lui envoyons une sélection de photos avec lui issues de nos archives depuis plusieurs années.



Nous n'avons pas inventé un vélo, nous avons pris la célèbre bibliothèque dlib et avons reçu des plongements (représentations vectorielles) de chaque personne. 



Nous avons ajouté un bot Telegram pour plus de commodité, et tout était super. Du point de vue des algorithmes de reconnaissance faciale, tout fonctionnait à merveille, mais la conférence était terminée et je ne voulais pas me séparer des technologies éprouvées. Nous voulions passer de plusieurs milliers de personnes à des centaines de millions, mais nous n'avions pas de mission commerciale spécifique. Après un certain temps, nos collègues ont eu une tâche qui nécessitait de travailler avec des quantités de données aussi importantes.



La question était d'écrire un système de surveillance de bot intelligent à l'intérieur du réseau Instagram. Ici, notre réflexion a donné lieu à une approche simple et complexe: La



manière simple: considérez tous les comptes qui ont beaucoup plus d'abonnements que d'abonnés, pas d'avatars, le nom complet n'est pas rempli, etc. En conséquence, nous obtenons une foule incompréhensible de comptes à moitié morts.



La manière difficile: puisque les robots modernes sont devenus beaucoup plus intelligents et qu'ils publient maintenant des messages, dorment et même écrivent du contenu, la question se pose: comment les attraper? Tout d'abord, surveillez de près leurs amis, car ce sont souvent des robots, et suivez les photos en double. Deuxièmement, rarement un bot sait comment générer ses propres images (bien que cela soit possible), ce qui signifie que les photos en double de personnes dans différents comptes sur Instagram sont un bon déclencheur pour trouver un réseau de robots.

Et après?

Si un chemin simple est assez prévisible et donne rapidement des résultats, alors un chemin difficile est difficile précisément parce que pour le mettre en œuvre, nous devrons vectoriser et indexer des volumes incroyablement importants de photographies pour des comparaisons ultérieures de similitudes - des millions, voire des milliards. Comment le mettre en pratique? Après tout, des questions techniques se posent:

1. Vitesse et précision de recherche
2. Espace disque utilisé par les données
3. La taille de la RAM utilisée. 

S'il n'y avait que quelques photos, au moins pas plus de dix mille, nous pourrions nous limiter à des solutions simples avec regroupement de vecteurs, mais pour travailler avec d'énormes volumes de vecteurs et trouver les voisins les plus proches d'un certain vecteur, des algorithmes complexes et optimisés sont nécessaires.



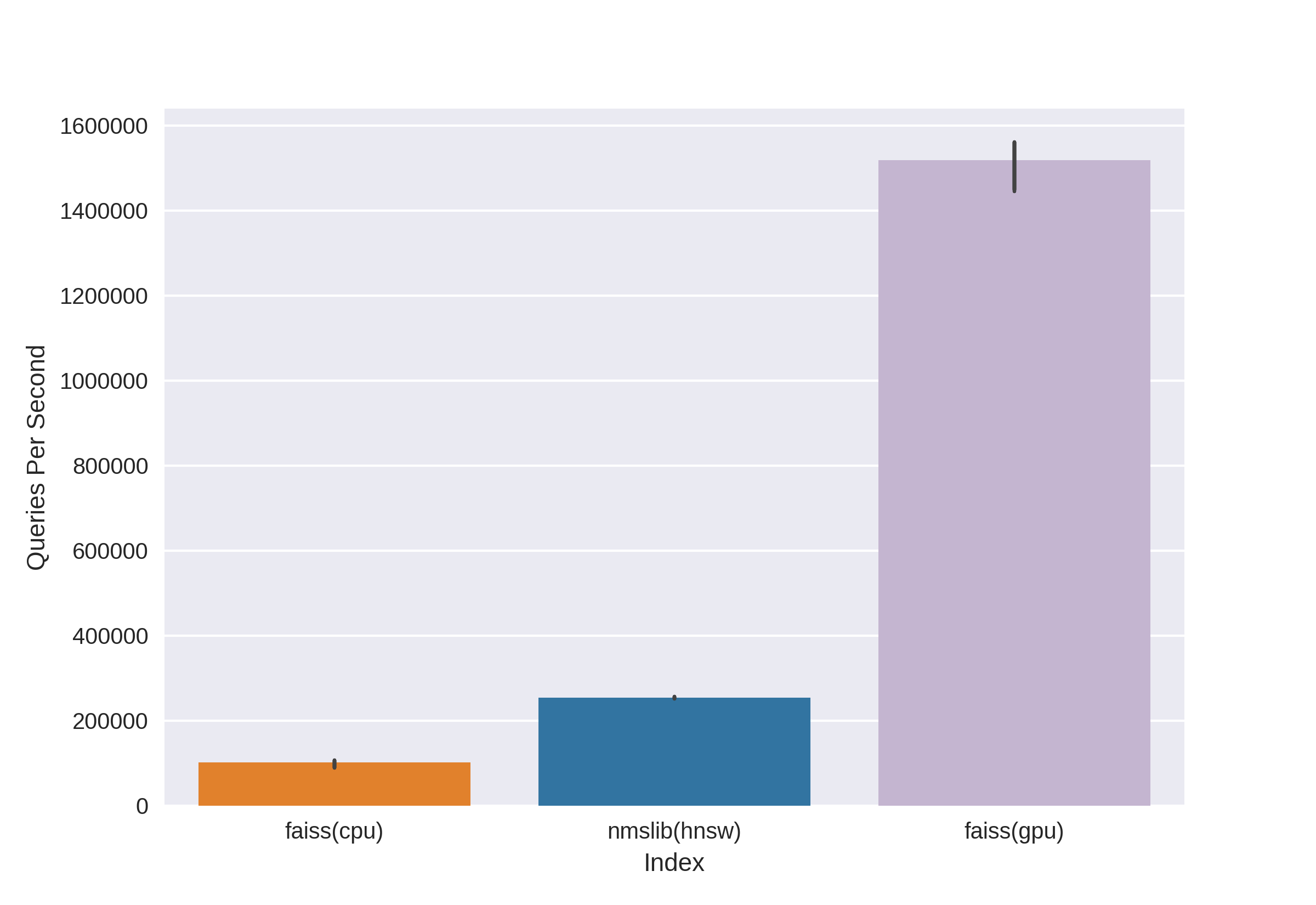
Il existe des technologies bien connues et éprouvées, telles que Annoy, FAISS, HNSW. L'algorithme de recherche rapide des voisins HNSW disponible dans les bibliothèques nmslib et hnswlib, montre des résultats de pointe sur le processeur, qui peuvent être vus à partir des mêmes benchmarks. Mais nous le coupons tout de suite, car nous ne sommes pas satisfaits de la quantité de mémoire utilisée lorsque nous travaillons avec de très grandes quantités de données. Nous avons commencé à choisir entre Annoy et FAISS et avons finalement choisi FAISS pour des raisons de commodité, moins d'utilisation de la mémoire, une utilisation potentielle sur le GPU et des critères de performance (vous pouvez voir, par exemple, ici ). D'ailleurs, dans FAISS, l'algorithme HNSW est implémenté en option.

Qu'est-ce que FAISS?

Facebook AI Research Similarity Search - Développé par l'équipe Facebook AI Research pour trouver rapidement les voisins les plus proches et les regrouper dans l'espace vectoriel. La recherche à grande vitesse vous permet de travailler avec de très grandes données - jusqu'à plusieurs milliards de vecteurs.



Le principal avantage de FAISS est ses résultats de pointe sur le GPU, tandis que son implémentation sur le CPU est légèrement inférieure à hnsw (nmslib). Nous voulions pouvoir rechercher à la fois sur le CPU et le GPU. De plus, FAISS est optimisé en termes d'utilisation de la mémoire et de recherche sur de grands lots.



La source



FAISS permet de trouver rapidement les k vecteurs les plus proches pour un vecteur x donné. Mais comment fonctionne cette recherche sous le capot?

Indices

Le concept principal de FAISS est l' index et, en fait, il ne s'agit que d'une collection de paramètres et de vecteurs. Les jeux de paramètres sont complètement différents et dépendent des besoins de l'utilisateur. Les vecteurs peuvent rester inchangés ou être réorganisés. Certains indices sont disponibles pour le travail immédiatement après leur avoir ajouté des vecteurs, et certains nécessitent une formation préalable. Les noms de vecteur sont stockés dans l'index: soit dans la numérotation de 0 à n, soit sous la forme d'un nombre qui correspond au type Int64.



Le premier index, et le plus simple que nous avons utilisé lors de la conférence, est Flat . Il ne stocke que tous les vecteurs en lui-même, et la recherche d'un vecteur donné est effectuée par recherche exhaustive, il n'est donc pas nécessaire de l'entraîner (mais plus sur l'entraînement ci-dessous). Avec une petite quantité de données, un index aussi simple peut couvrir entièrement les besoins de la recherche.



Exemple:

import numpy as np
dim = 512  #     512
nb = 10000  #    
nq = 5 #      
np.random.seed(228)
vectors = np.random.random((nb, dim)).astype('float32')
query = np.random.random((nq, dim)).astype('float32')

Créez un index plat et ajoutez des vecteurs sans formation:

import faiss
index = faiss.IndexFlatL2(dim)
print(index.ntotal)  #   
index.add(vectors)
print(index.ntotal)  #    10 000 

Nous trouvons maintenant 7 voisins les plus proches pour les cinq premiers vecteurs à partir de vecteurs:

topn = 7
D, I = index.search(vectors[:5], topn)  #  : Distances, Indices
print(I)
print(D)

On voit que les plus proches voisins avec une distance de 0 sont les vecteurs eux-mêmes, les autres sont rangés en augmentant la distance. Cherchons nos vecteurs à partir de la requête:

D, I = index.search(query, topn) 
print(I)
print(D)

Maintenant, les distances dans la première colonne des résultats ne sont pas nulles, car les vecteurs de la requête ne sont pas dans l'index.



L'index peut être enregistré sur le disque puis chargé à partir du disque:

faiss.write_index(index, "flat.index")
index = faiss.read_index("flat.index")

Il semblerait que tout soit élémentaire! Quelques lignes de code - et nous avons déjà une structure de recherche par vecteurs de grande dimension. Mais un tel index avec seulement des dizaines de millions de vecteurs de dimension 512 pèsera environ 20 Go et occupera autant de RAM lorsqu'il est utilisé.



Dans le projet de la conférence, nous avons utilisé une telle approche de base avec un index plat, tout était super en raison de la quantité relativement faible de données, mais maintenant nous parlons de dizaines et de centaines de millions de vecteurs de haute dimension!

Accélérez les recherches avec les listes inversées

Source



La caractéristique principale et la plus cool de FAISS est l'index de FIV, ouindex de fichier inversé . L'idée des fichiers inversés est laconique et magnifiquement expliquée sur les doigts :



imaginons une armée gigantesque, composée des guerriers les plus hétéroclites, comptant, disons, 1 000 000 de personnes. Il sera impossible de commander toute l'armée à la fois. Comme il est d'usage dans les affaires militaires, nous devons diviser notre armée en sous-unités. Divisons par$$$\sqrt{1 000 000} = 1000$parties à peu près égales, en choisissant pour le rôle des commandants un représentant de chaque unité. Et nous essaierons d'envoyer des caractères aussi similaires que possible en termes de caractère, d'origine, de données physiques, etc. soldats dans une unité, et nous sélectionnons le commandant afin qu'il représente son unité aussi précisément que possible - il était quelqu'un de «moyen». En conséquence, notre tâche a été réduite de commander un million de soldats à commander 1 000 unités par l'intermédiaire de leurs commandants, et nous avons une excellente idée de la composition de notre armée, car nous savons à quoi ressemblent les commandants.



C'est l'idée derrière l'indice FIV: regroupons un grand ensemble de vecteurs pièce par pièce en utilisant l'algorithme k-means, mettant en correspondance chaque partie un centroïde, est un vecteur qui est le centre choisi pour un cluster donné. La recherche sera effectuée à travers la distance minimale au centre de gravité, et ce n'est qu'alors que nous rechercherons les distances minimales parmi les vecteurs du cluster qui correspond au centre de gravité donné. Prendre k égal$$$\sqrt{n}$où $$$n$ - le nombre de vecteurs dans l'index, nous obtiendrons une recherche optimale à deux niveaux - premier parmi $$$\sqrt{n}$ centroïde puis parmi $$$\sqrt{n}$vecteurs dans chaque cluster. La recherche, par rapport à la recherche exhaustive, est accélérée plusieurs fois, ce qui résout l'un de nos problèmes lorsque l'on travaille avec plusieurs millions de vecteurs.





L'espace vectoriel est divisé par la méthode des k-moyennes en k grappes. Chaque cluster se voit attribuer un



code d'exemple de centre de gravité:

dim = 512
k = 1000  #  “”
quantiser = faiss.IndexFlatL2(dim) 
index = faiss.IndexIVFFlat(quantiser, dim, k)
vectors = np.random.random((1000000, dim)).astype('float32')  # 1 000 000 “”

Ou vous pouvez l'écrire beaucoup plus élégamment, en utilisant la chose FAISS pratique pour construire un index:

index = faiss.index_factory(dim, “IVF1000,Flat”)
 :
print(index.is_trained)   # False.
index.train(vectors)  # Train    
 
#  ,      ,      :
print(index.is_trained)  # True
print(index.ntotal)   # 0
index.add(vectors)
print(index.ntotal)   # 1000000

Après avoir examiné ce type d'index après Flat, nous avons résolu l'un de nos problèmes potentiels: la vitesse de recherche, qui devient plusieurs fois plus lente par rapport à une recherche complète.

D, I = index.search(query, topn) 
print(I)
print(D)

Mais il y a un "mais" - la précision de la recherche, ainsi que la vitesse, dépendra du nombre de clusters visités, qui peut être défini à l'aide du paramètre nprobe:

print(index.nprobe)  # 1 –           
index.nprobe = 16  #   -16    top-n  
D, I = index.search(query, topn) 
print(I)
print(D)

Comme vous pouvez le voir, après avoir augmenté nprobe, nous avons des résultats complètement différents, le sommet des distances les plus courtes en D est devenu meilleur.



Vous pouvez prendre nprobe égal au nombre de centroïdes dans l'index, alors cela équivaudra à une recherche par force brute, la précision sera la plus élevée, mais la vitesse de recherche diminuera sensiblement.

Recherche sur le disque - Listes inversées sur disque

Très bien, nous avons résolu le premier problème, maintenant nous obtenons une vitesse de recherche acceptable sur des dizaines de millions de vecteurs! Mais tout cela est inutile tant que notre énorme index ne rentre pas dans la RAM.



Spécifiquement pour notre tâche, le principal avantage de FAISS est la possibilité de stocker des listes inversées de l'index IVF sur le disque, en ne chargeant que les métadonnées dans la RAM.



Comment créer un tel index: nous formons indexIVF avec les paramètres nécessaires sur la quantité maximale possible de données qui tiennent en mémoire, puis ajoutons des vecteurs (ceux qui ont été entraînés et pas seulement) à l'index entraîné par parties et écrivons l'index pour chacune des parties sur le disque.

index = faiss.index_factory(512, “,IVF65536, Flat”, faiss.METRIC_L2)

La formation sur l'indice GPU est effectuée de cette manière:

res = faiss.StandardGpuResources()
index_ivf = faiss.extract_index_ivf(index)
index_flat = faiss.IndexFlatL2(512)
clustering_index = faiss.index_cpu_to_gpu(res, 0, index_flat)  #  0 –  GPU
index_ivf.clustering_index = clustering_index

faiss.index_cpu_to_gpu (res, 0, index_flat) peut être remplacé par faiss.index_cpu_to_all_gpus (index_flat) pour utiliser tous les GPU ensemble.



Il est hautement souhaitable que l'échantillon d'apprentissage soit aussi représentatif que possible et ait une distribution uniforme, c'est pourquoi nous pré-composons l'ensemble de données d'apprentissage à partir du nombre requis de vecteurs, en les sélectionnant au hasard dans l'ensemble de données.

train_vectors = ...  #     
index.train(train_vectors)

#    ,   :
faiss.write_index(index, "trained_block.index") 

#       
#      :
for bno in range(first_block, last_block+ 1):
    block_vectors = vectors_parts[bno]
    block_vectors_ids = vectors_parts_ids[bno]  # id ,  
    index = faiss.read_index("trained_block.index")
    index.add_with_ids(block_vectors, block_vectors_ids)
    faiss.write_index(index, "block_{}.index".format(bno))

Après cela, nous unissons toutes les listes inversées. Ceci est possible, puisque chacun des blocs est essentiellement le même index entraîné, juste avec différents vecteurs à l'intérieur.

ivfs = []
for bno in range(first_block, last_block+ 1):
    index = faiss.read_index("block_{}.index".format(bno), faiss.IO_FLAG_MMAP)
    ivfs.append(index.invlists)
    #  index   inv_lists 
    #        :
    index.own_invlists = False

#   :
index = faiss.read_index("trained_block.index")

#   invlists
#  invlists       merged_index.ivfdata
invlists = faiss.OnDiskInvertedLists(index.nlist, index.code_size, "merged_index.ivfdata")
ivf_vector = faiss.InvertedListsPtrVector() 

for ivf in ivfs: 
    ivf_vector.push_back(ivf)

ntotal = invlists.merge_from(ivf_vector.data(), ivf_vector.size())
index.ntotal = ntotal  #     
index.replace_invlists(invlists)  
faiss.write_index(index, data_path + "populated.index")  #    

Bottom line: maintenant notre index est populated.index et fichiers merged_blocks.ivfdata .



Dans populated.index enregistré le chemin complet d'origine vers le fichier avec les listes inversées, donc si le chemin du fichier ivfdata pour une raison quelconque, le changement de lecture de l'index devra utiliser l'indicateur faiss.IO_FLAG_ONDISK_SAME_DIR , qui vous permet de rechercher le fichier ivfdata dans le même répertoire que le populated.index:

index = faiss.read_index('populated.index', faiss.IO_FLAG_ONDISK_SAME_DIR)

L' exemple de démonstration de Github du projet FAISS a été pris comme base .



Un mini-guide pour choisir un index peut être trouvé dans le FAISS Wiki . Par exemple, nous avons pu intégrer un ensemble de données d'apprentissage de 12 millions de vecteurs dans la RAM, nous avons donc choisi l'indice IVFFlat sur 262144 centroïdes pour ensuite passer à des centaines de millions. Le guide propose également d'utiliser l'index IVF262144_HNSW32, dans lequel le vecteur appartenant au cluster est déterminé par l'algorithme HNSW avec 32 voisins les plus proches (en d'autres termes, le quantificateur IndexHNSWFlat est utilisé), mais, comme il nous a semblé lors de tests ultérieurs, la recherche d'un tel indice est moins précise. En outre, il convient de garder à l'esprit qu'un tel quantificateur élimine la possibilité d'utilisation sur le GPU.

Utilisation du disque considérablement réduite grâce à la quantification du produit

Grâce à la méthode de recherche sur disque, il était possible de supprimer la charge de la RAM, mais l'index avec un million de vecteurs occupait encore environ 2 Go d'espace disque, et nous discutons de la possibilité de travailler avec des milliards de vecteurs, ce qui nécessiterait plus de deux To! Bien sûr, le volume n'est pas si important si vous définissez un objectif et allouez de l'espace disque supplémentaire, mais cela nous dérange un peu.



Et ici, le codage vectoriel vient à la rescousse, à savoir la quantification scalaire (SQ) et la quantification de produit (PQ)... SQ est le codage de chaque composante vectorielle avec n bits (généralement 8, 6 ou 4 bits). Nous considérerons l'option PQ, car l'idée d'encoder un composant float32 avec huit bits semble trop déprimante en termes de perte de précision. Bien que dans certains cas, la compression de SQfp16 en float16 soit presque sans perte de précision.



L'essence de la quantification du produit est la suivante: les vecteurs de dimension 512 sont divisés en n parties, dont chacune est regroupée en 256 clusters possibles (1 octet), c'est-à-dire nous représentons un vecteur avec n octets, où n est généralement au plus 64 dans une implémentation FAISS. Mais une telle quantification n'est pas appliquée aux vecteurs de l'ensemble de données lui-même, mais aux différences de ces vecteurs et des centroïdes correspondants obtenus lors de la génération des listes inversées! Il s'avère que les listes inversées seront des ensembles de distances codées entre les vecteurs et leurs centroïdes.

index = faiss.index_factory(dim, "IVF262144,PQ64", faiss.METRIC_L2)

Il s'avère que maintenant nous n'avons pas besoin de stocker tous les vecteurs - il suffit d'allouer n octets par vecteur et 2048 octets par vecteur centroïde. Dans notre cas, nous avons pris$$$n = 64$, c'est à dire $$$\frac{512}{64} = 8$- la longueur d'un sous-vecteur, qui est définie dans l'un des 256 groupes.







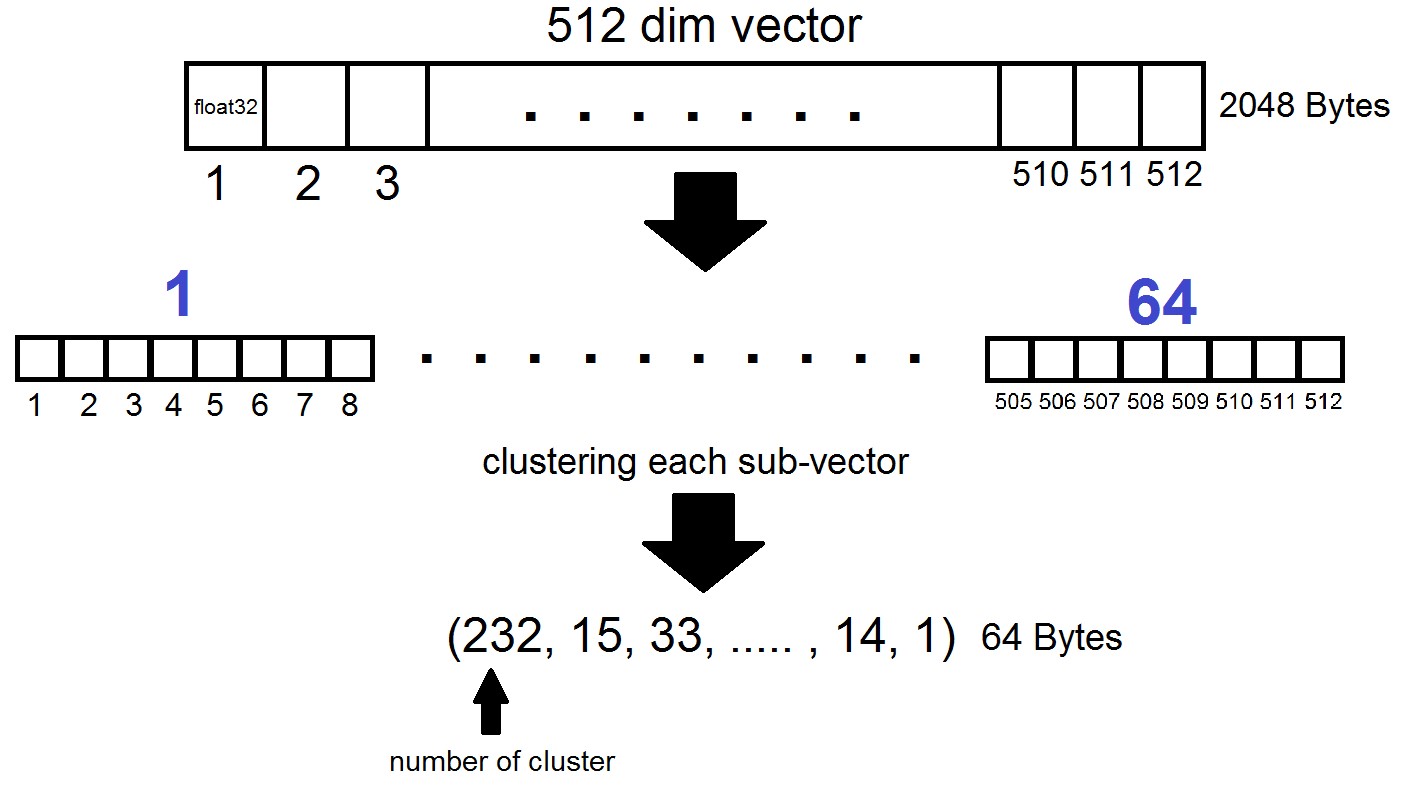
Lors de la recherche par le vecteur x, les centroïdes les plus proches seront déterminés d'abord avec le quantificateur Flat habituel, puis x est également divisé en sous-vecteurs, chacun étant codé par le numéro de l'un des 256 centroïdes correspondants. Et la distance au vecteur est définie comme la somme de 64 distances entre les sous-vecteurs.

Quel est le résultat?

Nous avons arrêté nos expériences sur l'index "IVF262144, PQ64", car il satisfaisait pleinement tous nos besoins en termes de vitesse de recherche et de précision, et nous avons également assuré une utilisation raisonnable de l'espace disque lors de la mise à l'échelle de l'index. Plus précisément, pour le moment, avec 315 millions de vecteurs, l'index occupe 22 Go d'espace disque et environ 3 Go de RAM en cours d'utilisation.



Un autre détail intéressant que nous n'avons pas mentionné précédemment est la métrique utilisée par l'indice. Par défaut, les distances entre deux vecteurs quelconques sont calculées dans la métrique euclidienne L2, ou dans un langage plus compréhensible, les distances sont calculées comme la racine carrée de la somme des carrés des différences de coordonnées. Mais vous pouvez spécifier une autre métrique, en particulier, nous avons testé la métrique METRIC_INNER_PRODUCT, ou métrique des distances de cosinus entre les vecteurs. Il est cosinus car le cosinus de l'angle entre deux vecteurs dans le système de coordonnées euclidien est exprimé comme le rapport du produit scalaire (en termes de coordonnées) des vecteurs au produit de leurs longueurs, et si tous les vecteurs de notre espace ont une longueur 1, alors le cosinus de l'angle sera exactement égal au produit en coordonnées. Dans ce cas, plus les vecteurs sont proches dans l'espace, plus leur produit scalaire sera proche de l'un.



La métrique L2 a une transition mathématique directe vers la métrique du produit scalaire. Cependant, lors de la comparaison expérimentale des deux métriques, l'impression était que la métrique des produits scalaires nous aide à analyser les coefficients de similitude des images de manière plus efficace. De plus, les plongements de nos photos ont été obtenus en utilisantInsightFace , qui implémente l'architecture ArcFace à l' aide de distances cosinus. Il existe également d'autres métriques dans les index FAISS que vous pouvez lire ici .

Conclusion et exemples curieux

Donc, revenons là où tout a commencé. Et cela a commencé, rappelons-le, avec la motivation de résoudre le problème de la recherche de bots sur le réseau Instagram, et plus précisément - de rechercher des messages en double avec des personnes ou des avatars dans certains groupes d'utilisateurs. Au cours du processus d'écriture du matériel, il est devenu clair qu'une description détaillée de notre méthodologie de recherche de robots nécessiterait un article séparé, que nous discuterons dans les publications suivantes, mais pour l'instant, nous nous limiterons à des exemples de nos expériences avec FAISS.



Vous pouvez vectoriser des images ou des visages de différentes manières, nous avons choisi la technologie InsightFace (vectoriser des images et en extraire des caractéristiques à n dimensions est une longue histoire à part). Au cours des expériences avec l'infrastructure que nous avons obtenue, des propriétés plutôt intéressantes et amusantes ont été découvertes.



Par exemple, après avoir obtenu la permission de collègues et de connaissances, nous avons téléchargé leurs visages dans la recherche et avons rapidement trouvé des photos dans lesquelles ils sont présents:





notre collègue a pris une photo d'un visiteur du Comic-Con, étant à l'arrière-plan dans une foule. Source





Pique-nique dans un grand groupe d'amis, photo du compte d'un ami. Source





Je viens de passer. Un photographe inconnu a capturé les gars pour son profil thématique. Ils ne savaient pas où était passée leur photo et après 5 ans, ils ont complètement oublié comment ils avaient été photographiés. Source





Dans ce cas, le photographe est inconnu et photographié en secret!

A immédiatement rappelé la fille suspecte avec SLR, assise en ce moment devant :) Source



Ainsi, par de simples actions, FAISS vous permet d'assembler sur votre genou un analogue du célèbre FindFace.



Autre particularité intéressante: dans l'indice FAISS, plus les faces se ressemblent, plus les vecteurs correspondants dans l'espace sont proches les uns des autres. J'ai décidé de regarder de plus près les résultats de recherche légèrement moins précis sur mon visage et j'ai trouvé des clones terriblement similaires à moi :)





Certains des clones de l'auteur.

Sources photographiques: 1 , 2 ,  3 De



manière générale, FAISS ouvre un immense champ pour la mise en œuvre de toute idée créative. Par exemple, en utilisant le même principe de proximité vectorielle de faces similaires, on pourrait construire des chemins d'une personne à une autre. Ou, en dernier recours, faites de FAISS une usine pour la production de tels mèmes:





Source



Merci pour votre attention et nous espérons que ce matériel sera utile aux lecteurs de Habr!



L'article a été écrit avec le soutien de mes collègues Artyom Korolev (Korolevart), Timur Kadyrov et Arina Reshetnikova.



R&D Réseau Dentsu Aegis Russie.