AES est la norme de cryptage américaine. Partie III

Le motif de la publication de textes aussi détaillés sur la norme AES est de fournir une opportunité de vous familiariser avec elle en détail, suffisante non seulement pour développer une implémentation logicielle indépendante de l'algorithme de chiffrement, mais aussi pour créer des algorithmes pour d'éventuelles attaques cryptanalytiques sur le chiffrement, c'est-à-dire pour déchiffrer des chiffrements sans connaître la clé ...



Les publications disponibles sur le réseau ne répondent pas à ces objectifs et ne peuvent pas être utilisées par moi dans le processus de formation de spécialistes.



L'une des principales exigences anciennes (voire anciennes) pour les chiffrements est de créer un algorithme de chiffrement ouvert (accessible pour étude) et d'enrouler autour de lui (modes, protocoles, etc.) tout sauf la clé de chiffrement. La clé est quelque chose qui doit être gardé dans la plus stricte confiance de chacun. Dans ce cas, la clé ne doit pas être classée comme "secrète". La limite d'une telle condition est que seul le destinataire du cryptogramme possède la clé, lui-même, en principe, doit la fixer.



Pour les systèmes de chiffrement symétriques, cette condition n'est pas réalisable. Et c'est la différence fondamentale entre les systèmes asymétriques (à deux clés) et les systèmes symétriques, dans lesquels la source de fuite d'informations clés n'est peut-être pas la seule. Il a été noté plus tôt qu'AES est une version simplifiée du chiffrement RIJNDAEL, et ici nous utiliserons la version complète par endroits.

AES (Key Schedule).

Le choix d'une clé lors du chiffrement d'un message est une tâche responsable. L'approche générale est qu'un vecteur binaire aléatoire dans un espace vectoriel multidimensionnel est choisi et utilisé pour la clé. Souvent, un certain nombre d'algorithmes de chiffrement et de chiffrements sont caractérisés par la présence de clés faibles ou invalides, qui sont révélées soit pendant le développement des chiffrements, soit pendant leur fonctionnement lors de recherches supplémentaires. algorithmes par des auteurs ou analystes cryptographes et, par conséquent, des publications à ce sujet.



À son tour, cela impose des restrictions sur la procédure de génération de clés, ce qui n'est pas souhaitable car cela la complique. Les fondements mathématiques concernant le chiffrement sont très similaires aux fondements mathématiques de la génération de clés, et vous pouvez en savoir plus à leur sujet ici .



Le vecteur binaire sélectionné est appelé la clé de chiffrement et il est converti en un «carré» de 4 × 4 = 16 octets. Ensuite, des clés rondes sont formées à partir de celle-ci à l'aide de deux procédures spéciales, qui sont utilisées dans les processus de cryptage / décryptage, qui sont décrites en détail ici .



Une procédure est appelée extension de clé, l'autre est appelée sélection de clé ronde. Un vecteur binaire aléatoire sélectionné avec une longueur fixe est développé. Il est également important d'examiner attentivement le choix d'un capteur de nombres aléatoires, d'effectuer ses tests et ses tests.

Extension clé

Le fait d'agrandir la clé d'origine (sélectionnée) est de la diviser en non-blocs (32 bits chacun), puis de générer à partir d'eux de nombreux nouveaux blocs de même longueur pour chaque tour.

Donc, laissez la clé de chiffrement sélectionnée (128 bits) AES = 2b 7e 15 16 28 ae d2 a6 ab f7 15 88 09 cf 4f 3c, pour Nk = 4, qui est représentée par blocs de 4 octets et son extension ronde initiale est w [0 ] = 2b7e1516; w [1] = 28aed2a6; w [2] = abf71588; w [3] = 09cf4f3c. Le symbole w [i] dans la table QC, i = 0 (1) 43, désigne une colonne de 4 octets de la clé ronde.



Une session de chiffrement est la préparation et la transformation algorithmique d'un message, comme une lettre. Le texte de la lettre en représentation binaire est divisé en blocs de longueur fixe Nb = 128, 192 ou 256 bits. Dans la norme AES, la longueur du bloc n'est que de 128 bits.



Ensuite chaque bloc est représenté par un carré ou (rectangle à 4 lignes) et est chiffré séparément pour un nombre fixe de tours Nr = Nr (Nb, Nk), qui est fonction de deux variables: la longueur du bloc Nb et la longueur de la clé Nk, qui peut prendre des valeurs indépendamment 128, 192, 256 bits.



Le choix de la clé de chiffrement n'impose aucune restriction sur la séquence de bits elle-même. Chacun des Nr tours utilise sa propre clé ronde préformée ou calculée directement {w [i]}.



Les clés rondes sont formées à partir de la clé de chiffrement à l'aide d'un algorithme spécial, qui comprend la procédure d'extension de clé et la procédure de sélection de clé ronde. La spécification directe des clés rondes, en contournant ces procédures, est inacceptable.



L'essence et le but de la première procédure est de convertir une clé de chiffrement d'origine donnée en une clé plus longue et étendue (clé étendue). Le nombre total de bits de la clé étendue à partir de laquelle les clés rondes sont sélectionnées est déterminé par le produit K = Nk (Nr + 1) - le nombre de bits dans le bloc de clés est multiplié par le nombre de tours, augmenté d'une unité.



Exemple 1 . Soit Nb = Nk = 4, blocs donnés de longueur 4 × 32 = 128 bits, alors Nr = 10.

Longueur K en bits pour la clé étendue K = 128 ∙ 11 = 1408 bits.



La deuxième procédure (RoundKey Selection) est une sélection séquentielle de 32Nk, soit 4 mots de 32 bits à partir de la clé étendue, c'est-à-dire que la première touche ronde est représentée par les Nk mots initiaux nouvellement formés, la deuxième touche ronde est représentée par les Nk mots suivants, et ainsi jusqu'au dernier tour.



Exemple 2... Avec les mêmes données initiales (voir l'exemple précédent), la longueur totale de la clé étendue en octets contient Nk (Nr + 1) = 4 ∙ 11 = 44 mots de quatre octets W (i),

i = 0 (1) Nk (Nr + 1) - 1 Les lignes de la table QC sont numérotées par des nombres naturels. La première ligne a le numéro 4, car 4 lignes (avec les numéros 0,1,2,3) avec une clé de chiffrement ne sont pas incluses dans le tableau QC.



Tableau Clé de chiffrement AES pour les 10 tours (voir tableau QC ci-dessous).







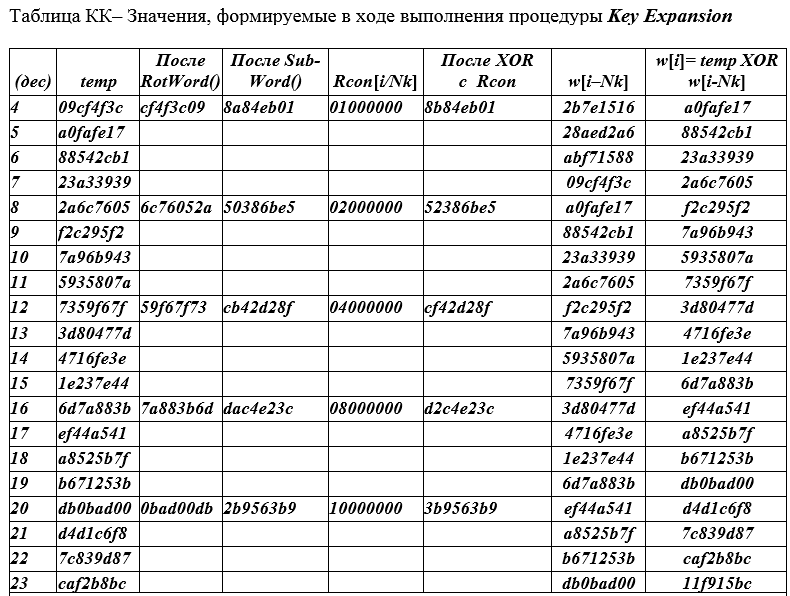
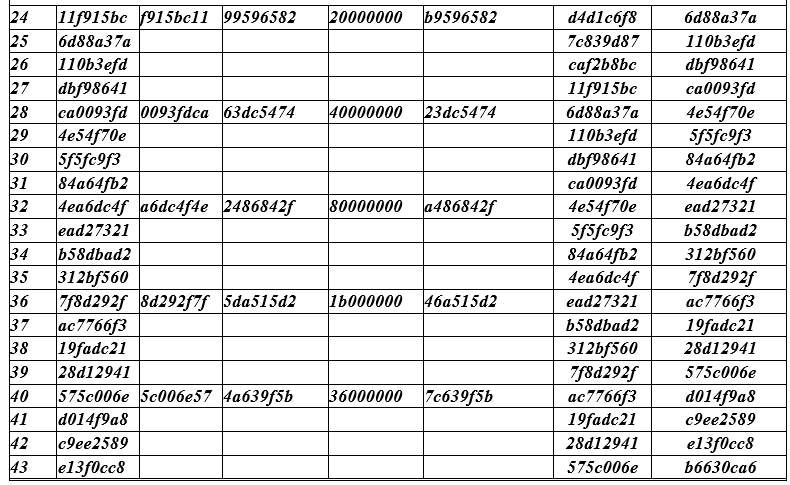
Les lignes du tableau sont divisées en groupes (4 lignes chacun). Dans chaque groupe, tous les champs sont remplis sur une seule ligne du haut. Dans les trois lignes suivantes, seuls les champs extrêmes (gauche et droite) sont remplis. Le champ gauche ( temp ) de la ligne suivante et des deux lignes suivantes contient les valeurs tirées du champ droit de la ligne au-dessus.



Donnons un exemple de remplissage de la première ligne avec le nombre i = 4 de la table QC. Colonne de gauche - les numéros de ligne actuels commencent par la valeur (4) puisque les premières valeurs 0,1,2,3 ne sont pas incluses dans le tableau. En général, l'index (numéro de ligne) i court sur les valeurs i = 0 (1) Nk (Nr + 1) -1 ou i = 0 (1) 43 au total 44 mots de 32 bits.



Vers la colonne templa valeur w [i-1] = 09cf4f3c est placée et par rotation (décalage cyclique d'un octet) RotWord () nous obtenons la valeur CF4F3C09, qui est placée dans la 3ème colonne. La 4ème colonne contient le résultat de 8A84EB01 en remplaçant les octets de sous-octets des valeurs de la 3ème colonne , c'est-à-dire CF → 8A; 4F → 84; 3C → EB; 09 → 01 => 8A84EV01.



Chaque 4ème ligne du tableau dans la 5ème colonne est remplie avec la valeur Rcon [i / Nk], une constante calculée par la formule Rcon (J) = 01000000, j = [i / Nk] = 2 ^j-1 = 2 ⁰ = 1) la valeur 01 00 00 00 s'écrit sur 4 mots d'octets dont le premier octet est 2 ⁰ = 1, c'est-à-dire 0000 0001 ₂ , les octets restants de ce mot de 32 bits sont à zéro.



Le champ de la colonne 6 contient la somme (XOR) des 4e et 5e champs 8A84EB01 + 01000000 = 8B84EB01;

Le champ de la colonne 7 contient W [i - Nk] = W [4 - 4] = W [0] = 2B7E1516;

Le champ de la colonne 8 contient la somme des champs des colonnes 6 et 7 W [i = 4] = 884EB01 + 2B7E1516 = A0FAFE17;

Et maintenant, nous allons examiner les procédures nommées en détail et en détail.

Procédure d'extension de clé

Examinons en détail la procédure de génération d'une clé étendue à partir de la clé de chiffrement d'origine. Formellement, la clé étendue W sera décrite par une séquence de blocs W [i], i = 0 (1) Nk (Nr + 1) -1, mots de 4 octets (clés rondes) contenus dans la dernière colonne de la table KK, dans laquelle le premier Nk 32 bits les mots représentent la clé d'origine, c'est-à-dire

W = {W [0], W [1], W [2], W [3], W [4], ..., W [K-1]}



i-ième suivant les mots sont formés de manière récursive à partir de mots précédents conformément à une expression dans laquelle la sommation est XOR.



...



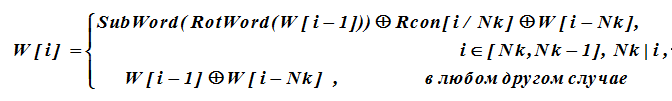Pour les mots clés W [i] dont l'indice est un multiple de Nk, les valeurs de W [i-1] sont soumises à une conversion supplémentaire avant d'effectuer l'opération XOR. Cette transformation est décrite comme suit.



La description de la conversion contient des fonctions:



RotWord () - décalage cyclique d'octets d'un mot de 32 bits a (0) a (1) a (2) a (3) selon la règle

{a (0) a (1) a (2) a (3)} → {a (3) a (0) a (1) a (2)};



SubWord () - remplacement d'octet a (j) par des éléments du bloc S de la fonction SubBytes (), par exemple, l'octet (af) est remplacé par l'octet s (a, f) du bloc S; l'action est la même que lors du traitement d'un message,

Rcon [j] - le terme XOR est égal à 2 ^j-1 .





Des multiples de Nb sont sélectionnés, dont les valeurs sont formées à l'aide des fonctions SubWord (), RotWord (), Rcon (). Les positions W [0] –W [3] sont remplies selon les données initiales données, toutes les suivantes sont calculées selon le rapport pour W [i].

Sélection de clé ronde

Sélection d'une touche ronde (RoundKeySelection). Pour le tour en cours avec le numéro r. La touche ronde est sélectionnée comme {W [Nb (r) -1], ..., W [Nb (r + 1) - 1]},

r = 1 (1) Nr.



Notez ici que l'algorithme de chiffrement général prévoit différentes variantes des ensembles de variables Nb, Nk, Nr. Pour une implémentation spécifique de l'option fixe, elle peut être grandement simplifiée. La clé ronde peut être calculée à la volée, ce qui ne nécessite pas une grande mémoire pour stocker toute la séquence W. Vous pouvez vous limiter à un tampon de Nk mots.



Exemple 3 . Expliquons les propositions théoriques données par un exemple numérique. Soit, comme précédemment, Nb = Nk = 4, Nr = 10. La clé de chiffrement est donnée sous la forme d'une séquence hexadécimale K = 2b7e1516 282ed2a6 abf71588 09cf4f3c







L'architecture «carrée» et le calcul orienté octets déterminent la forme de leur présentation dans le tableau suivant.





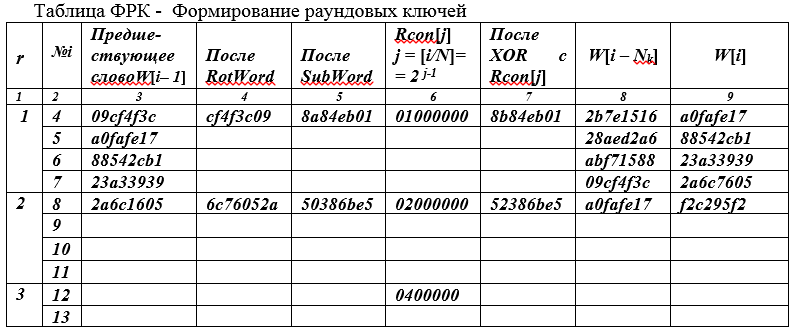
La colonne de gauche a été ajoutée au tableau - le numéro (r) du tour.

Dans la première ligne r = 1, i = 4, l'octet précédent W [i-1] = W [3] est écrit dans la troisième colonne, c'est-à-dire le dernier octet de la clé de chiffrement K. Puisque l'indice i = 4 est un multiple de Nk = 4, alors dans la colonne 6, nous écrivons (Rcon (J) = 01000000, j = [i / Nk] = 2 ^j-1 = 2 ⁰ = 1) la valeur 01 00 00 00 4- est écrite x mot d'octet, dont le premier octet est 2 ⁰ = 1, c'est-à-dire 0000 0001, les autres octets de ce mot de 32 bits sont nuls.



Dans la quatrième colonne du tableau, entrez les valeurs de la colonne précédente, mais décalées cycliquement de 1 octet vers la gauche (rotation des mots - RotWord). La cinquième colonne contient le résultat du remplacement d'octet des valeurs de la colonne précédente par les valeurs d'octets du bloc S (fonction SubWord - remplacer octets). Après cela, l'addition mod2 (XOR) est faite du contenu des colonnes 5 et 6, 8a84eb01 + 0100 0000 = 8b84eb01, et le résultat de la somme est entré dans la colonne 7.



Dans la représentation binaire de l'octet 0000 0001 ₂ = 01 _{16, les} bits _les moins significatifs sont situés sur la droite.



La colonne 8 contient la valeur du mot W [i-Nk] = W [0] (pour la première ligne, il s'agit de la valeur du premier mot de 4 octets (octet gauche) de la clé de chiffrement W [0]), qui est ajoutée par l'opération XOR 8b 84 eb 01+ 2b 7e 15 16 = a0 fa fe 17 avec le contenu de 7 colonnes. Le résultat de la somme (colonne 9) n'est que le premier des quatre mots de 4 octets de la clé ronde du premier tour.



Les trois autres mots de la clé ronde du premier tour sont formés sans utiliser la fonction de décalage cyclique, de remplacement et de Rcon [j], car leurs nombres ne sont pas des multiples de Nk. Le contenu de la colonne 9 est transféré dans la troisième colonne de la ligne suivante du tableau.



Défintion Rcon [j]. Cette procédure est effectuée selon un algorithme spécial, dont nous illustrerons les actions à l'aide d'exemples. L'argument j de la fonction Rcon [j] est un entier et est déterminé par la valeur courante de la variable i - le numéro du mot clé. Evidemment

j = 1, 2, 3,… pour i = Nk, 2Nk, 3Nk,….



Puisque Nk dans notre exemple est 4, nous avons des valeurs entières de j pour i = 4, 8, 12. De plus, pour chaque entier j, Rcon [j] = 2 ^j-1 = 1, 2, 4, 8, 16, ....

Le doublement est valide tant que Rcon [j] est un élément du champ GF (2 ⁸ ).



Pour i> 32, nous obtenons j> 8. Les valeurs en dehors du champ doivent être retournées au champ. Ceci est réalisé en réduisant la représentation polynomiale des éléments du champ Rcon [j] (modφ (x)).



Exemple 4. Soit i = 32, 36, 40. Alors j = 8, 9, 10. Ces valeurs sont en dehors du champ. Nous les remettons sur le terrain par réduction modulo φ (x) et calculons les valeurs requises.

Nous définissons les valeurs correspondantes de Rcon [j]. Les résultats des calculs sont résumés dans un tableau.





Ceci termine l'examen des étapes de génération de clés de chiffrement AES rondes.