Tri de tas

Ceci est le dernier article d'une série sur le tri de tas. Dans les conférences précédentes, nous avons examiné une grande variété de structures de tas qui montrent d'excellents résultats en termes de vitesse. Cela soulève la question: quel tas est le plus efficace en matière de tri? La réponse est: celle que nous allons examiner aujourd'hui.

EDISON .




— « » — -, CRM-, , iOS Android.



;-)

Les tas de fantaisie que nous avons examinés plus tôt sont bons, mais le tas le plus efficace est le tas standard avec une compensation améliorée.



Qu'est-ce qu'une compensation, pourquoi est-elle nécessaire dans un tas et comment elle fonctionne est décrite dans la toute première partie d'une série d'articles.



L'écran standard dans le tri classique par groupe fonctionne à peu près "front" - un élément de la racine du sous-arbre est envoyé au presse-papiers, les éléments de la branche, selon les résultats de la comparaison, montent. Tout est assez simple, mais il s'avère trop de comparaisons.







Dans la voie ascendante, les comparaisons sont enregistrées du fait que les parents sont à peine comparés à leurs descendants, fondamentalement, seuls les descendants sont comparés entre eux. Dans un tas régulier, le parent est comparé aux descendants et les descendants sont comparés les uns aux autres - par conséquent, les comparaisons sont presque une fois et demie plus avec le même nombre d'échanges.



Alors, comment cela fonctionne, regardons un exemple spécifique. Disons que nous avons un tableau dans lequel un tas est presque formé - il ne reste plus qu'à passer au crible la racine. Pour tous les autres nœuds, la condition est satisfaite - tout enfant n'est pas plus grand que son parent.



Tout d'abord, à partir du nœud pour lequel le tamisage est effectué, vous devez descendre, le long de grands descendants. Le tas est binaire - c'est-à-dire que nous avons un enfant gauche et un enfant droit. Nous descendons à la branche où le descendant est plus grand. À ce stade, le nombre principal de comparaisons se produit - les enfants gauche / droit sont comparés les uns aux autres.







Ayant atteint la feuille au dernier niveau, nous avons donc décidé de la branche, les valeurs dans lesquelles doivent être déplacées vers le haut. Mais vous n'avez pas besoin de déplacer la branche entière, mais uniquement la partie plus grande que la racine à partir de laquelle vous avez commencé.



Par conséquent, nous remontons la branche jusqu'au nœud le plus proche, qui est supérieur à la racine.







La dernière étape consiste à utiliser une variable de tampon pour déplacer les valeurs de nœud vers le haut de la branche.







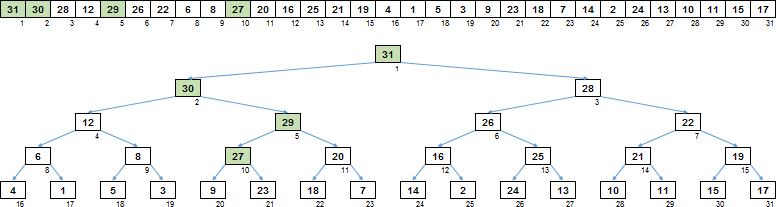
C'est tout. Une clairière ascendante a formé un arbre de tri à partir d'un tableau, dans lequel tout parent est supérieur à ses descendants.



Animation finale:

Implémentation Python 3.7

L'algorithme de tri de base n'est pas différent du tas standard:

#    
def HeapSortBottomUp(data):

    #    
    #   -   
    # (   )       
    for start in range((len(data) - 2) // 2, -1, -1):
        HeapSortBottomUp_Sift(data, start, len(data) - 1) 

    #        
    #        .
    for end in range(len(data) - 1, 0, -1): 
        #       
        #    
        data[end], data[0] = data[0], data[end]
        #        
        #   
        #     
        HeapSortBottomUp_Sift(data, 0, end - 1)
    return data

La descente vers la feuille inférieure est commodément / visuellement placée dans une fonction distincte:

#      
#   
def HeapSortBottomUp_LeafSearch(data, start, end):
    
    current = start
    
    #  ,  
    #  (  ) 
    while True:
        child = current * 2 + 1 #  
        #  ,    
        if child + 1 > end: 
            break 
        #  ,   
        if data[child + 1] > data[child]:
            current = child + 1
        else:
            current = child
    
    #  ,    
    child = current * 2 + 1 #  
    if child <= end:
        current = child
        
    return current

Et surtout - une clairière, d'abord descendante, puis émergeant vers le haut:

#  
def HeapSortBottomUp_Sift(data, start, end):
    
    #        
    current = HeapSortBottomUp_LeafSearch(data, start, end)
    
    #  ,    
    #     
    while data[start] > data[current]:
        current = (current - 1) // 2
    
    #   ,
    #      
    temp = data[current]
    data[current] = data[start]
    
    #        
    # -     
    while current > start:
        current = (current - 1) // 2
        temp, data[current] = data[current], temp  

De façon purement empirique - selon mes mesures, le tri croissant par tas est 1,5 fois plus rapide que le tri par tas normal.



Selon certaines informations (sur la page de l'algorithme sur Wikipedia, dans le PDF dans la section "Liens"), BottomUp HeapSort surpasse en moyenne même le tri rapide - pour des tableaux assez volumineux avec des tailles de plus de 16 mille éléments.

Liens

Tri en tas de bas en haut



Une variante du tri en tas avec un nombre presque optimal de comparaisons



Construction rapide de tas



Une nouvelle variante du tri en tas battant, en moyenne, un tri rapide (si n n'est pas très petit)

Articles de la série:

• Application Excel AlgoLab.xlsm
• Tri des échanges
• Trier les insertions
• Trier par sélection
  • Tris de tas: N-Pyramides
  • Heap Sorts: Numéros de Leonardo
  • Tris de tas: tas faible
  • Tri de lots: arbre cartésien
  • Heap Torts: arbre de tournoi
  • Tri de tas: effacement croissant
• Fusionner les tris
• Tri de distribution
• Tri hybride

Le tri d'aujourd'hui a été ajouté à l'application AlgoLab, qui l'utilise - mettez à jour le fichier Excel avec des macros.