
Merci beaucoup. Je m'excuse d'être assis ici. Je suis un très vieil homme.
Mon sujet aujourd'hui est en un sens très spécial, car il est très ancien. Les kinks font partie intégrante de la vie humaine, ils sont toujours là. Les anciens ont écrit à ce sujet. Cette chose est en grande partie hors de notre contrôle. Et dans un sens, ils semblent être un degré extrême de complication - juste un désordre complet.
Il existe de nombreux types de troubles. Ainsi, par pure coïncidence, j'ai commencé il y a de nombreuses années à faire face à cette forme de complication et, à ma grande surprise, j'ai trouvé des signes et, je dois dire, des signes d'ordre très clairs dans les plis. Je voudrais donc aujourd'hui vous présenter quelques exemples de ce que cela signifie. Je préfère le mot «cassé» à «inégal» car pour quelqu'un qui a étudié le latin, comme moi dans ma jeunesse lointaine, l'inégalité est l'opposé de la régularité. Mais ce n'est pas le cas.
L'égalité est l'opposé de la fracture, car le monde nous apparaît pour la plupart comme plein de fractures.
Laissez-moi vous montrer quelques objets. Certains d'entre eux sont créés artificiellement. D'autres sont très réels, dans un certain sens. C'est la vraie chose.

C'est du chou-fleur. Pourquoi est-ce que je vous montre du chou-fleur, une plante ordinaire et ancienne? Parce que, malgré sa routine et son antiquité, il est complexe et simple. c'est complexe et simple. Par exemple, il n'est pas difficile de le peser. Le poids compte si nous allons le manger. Mais supposons que nous allons mesurer sa surface. Cela devient intéressant. Après avoir coupé l'une des fleurs de chou-fleur avec un couteau bien aiguisé, et en regardant de près, nous voyons le chou-fleur entier, seulement d'une taille plus petite. Ensuite, vous pouvez couper encore et encore et encore et encore et encore ... Et vous obtenez des spécimens de plus en plus petits de chou-fleur. L'expérience humaine a montré qu'il existe des formes avec une propriété si intéressante que chaque partie est similaire au tout, mais de plus petite taille. Et qu'est-ce que la personne a appris de ce fait? Très peu.
Dans le cadre de l'étude de ce problème, j'ai découvert quelque chose de complètement étonnant: le kink peut être mesuré par un nombre, disons 2,3 ou 1,2, et parfois bien plus. Un jour, un de mes amis a apporté une photo et, à moitié en plaisantant, a demandé: "Quel est le pli de cette courbe?" J'ai dit: «Un peu moins d'un an et demi.» Il s'est avéré que c'était égal à 1,48. Cela ne m'a pas pris longtemps car j'ai étudié ces choses pendant si longtemps. Les chiffres en question indiquent le degré de fracture de la surface.

Permettez-moi de faire une réserve tout de suite que les surfaces sont absolument artificielles et ont été créées sur un ordinateur. Le seul point de départ était le nombre. Ce nombre est plié. La fracture à gauche est le résultat de la copie de plusieurs paysages. Sur la droite - j'ai moi-même mis un coude plus élevé. Si vous regardez de près, après un certain temps, vous pouvez reconnaître les différences entre ces deux cas à l'œil nu.
L'homme a dû s'habituer au concept de fracture. C'est très cassé, mais cela, pourrait-on dire, est lisse, mais c'est complètement lisse. Peu de choses sont très faciles. Posons-nous maintenant la question: quelle est la surface du chou-fleur? Il peut être mesuré et mesuré et mesuré ... Plus la mesure est précise, plus la surface est grande, et ainsi de suite, jusqu'à de très petites distances. Quelle est la longueur du littoral de ces lacs? Plus la mesure est précise, plus elle durera longtemps. Le concept de longueur du littoral, qui semble si évident parce qu'il est souvent cité, est en fait complètement faux: il n'y en a tout simplement pas. Il doit y avoir une approche différente.
Et quelle est l'utilité de ces connaissances? Étonnamment, les avantages sont nombreux. Pour commencer, les paysages artificiels que j'ai, dirons-nous, inventés sont constamment utilisés en cinématographie. Nous voyons des montagnes au loin. Ce sont peut-être des montagnes, mais ce ne sont peut-être que des formules fluides. C'est très facile à réaliser. Auparavant, cela prenait beaucoup de temps, mais maintenant c'est une bagatelle. Jetez un œil ici. C'est une vraie lumière.
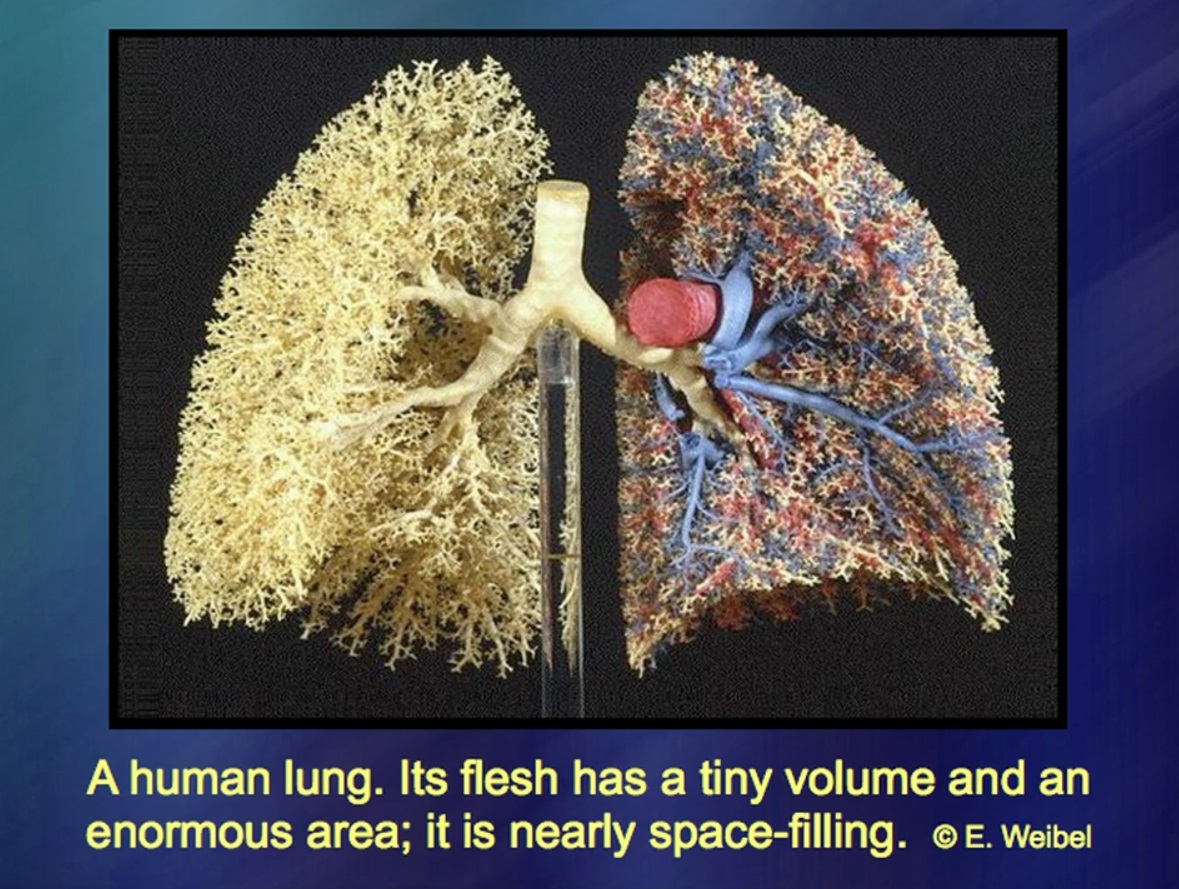
Le poumon est un objet très étrange. Nous savons tous très bien que cela a un certain poids. On sait également que le volume du poumon est très petit. Et la zone pulmonaire? Les anatomistes débattent depuis longtemps de cette question. On pense que chez un homme normal, la surface du poumon est égale à la surface d'un ballon de basket. D'autres soutiennent qu'il n'y a pas cinq balles de ce type. Les écarts sont colossaux. Pourquoi? Parce que la zone du poumon est un concept très vague. La branche et la branche des bronches sont de plus en plus profondes. Et ils cessent de se ramifier non pas à cause d'un principe, mais à cause de conditions purement physiques, à cause du mucus à l'intérieur du poumon. C'est ainsi qu'un poumon beaucoup plus gros se forme: les bronches se ramifient de plus en plus profondément, tandis que l'écart entre elles est à peu près le même pour une baleine, et pour une personne, et pour un petit rongeur.
Alors, à quoi cela sert-il? Étonnamment et même étonnamment, les anatomistes avaient une mauvaise idée de la structure du poumon jusqu'à récemment. Je pense que mes recherches mathématiques, de manière assez surprenante, ont été d'une grande aide pour les chirurgiens qui étudient les maladies pulmonaires, ainsi que les maladies du foie, où il existe de tels systèmes de branches avec un manque de géométrie intelligible. En d'autres termes, j'ai dû créer une géométrie pour quelque chose qui n'a pas sa propre géométrie. Une qualité surprenante a été trouvée: très souvent les règles de cette géométrie sont extrêmement concises. Vous commencez avec des formules courtes, appliquez-les plusieurs fois, parfois à plusieurs reprises, encore et encore. La même répétition. Et à la fin, il s'avère quelque chose comme ça.
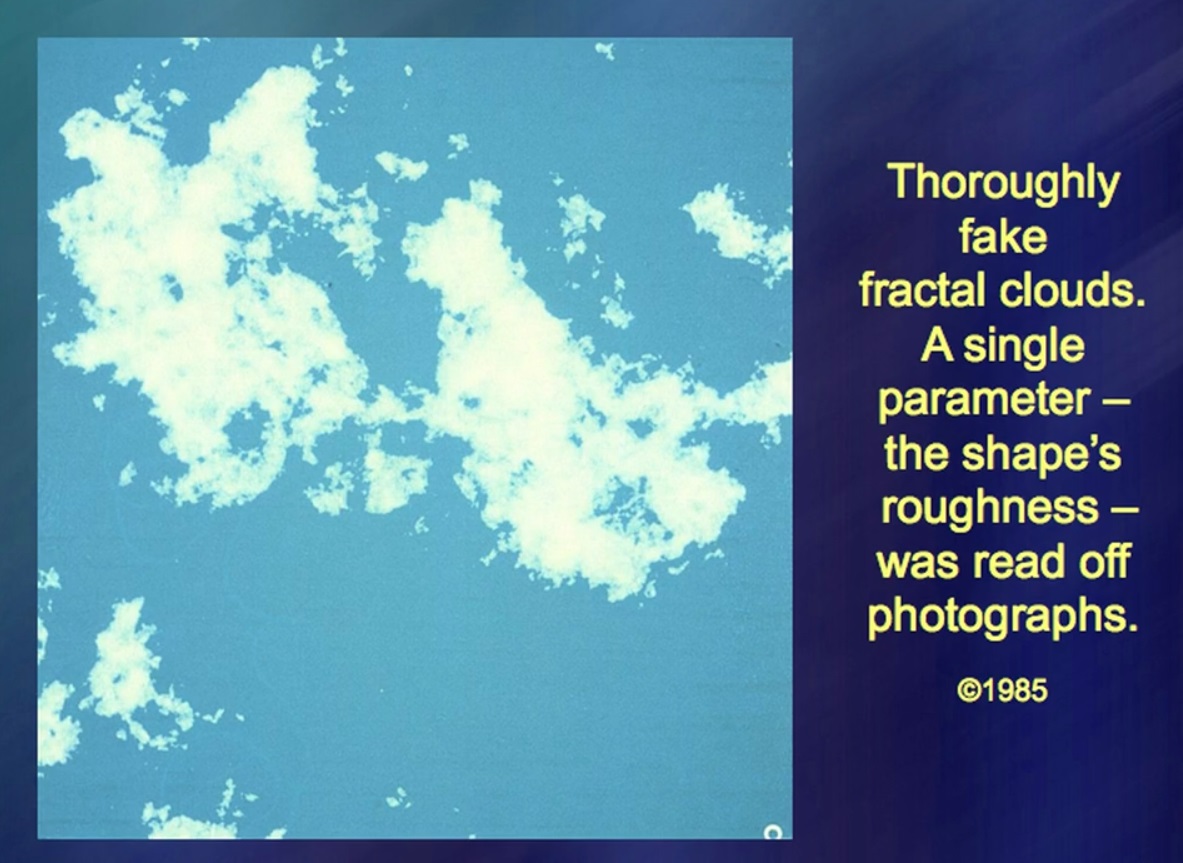
Ce nuage est complètement artificiel, à 100%. D'accord, 99,9%. Le seul élément naturel ici est le nombre, la fracture du nuage - ce nombre est tiré de la nature. Une chose aussi complexe qu'un nuage, si instable, changeante, obéit à une règle simple. Cette règle simple n'est pas une explication de la nébulosité. Mais la mer de nuages doit tenir compte de cette règle. Je ne sais pas à quel point ces vieilles photos sont parfaites. Je l'ai fait de manière intensive, mais mon attention s'est ensuite portée sur d'autres phénomènes.
Et voici une autre chose intéressante. L'un des événements révolutionnaires de l'histoire des mathématiques, insuffisamment apprécié par beaucoup, a eu lieu il y a environ 130 ans, il y a 145 ans. Les mathématiciens ont commencé à créer des formes inexistantes. Parmi les mathématiciens a commencé à être appréciée, et à un degré absolument inimaginable, la capacité d'une personne à créer quelque chose dont la nature n'a jamais existé. En particulier, ils ont pu inventer une courbe qui remplit tout le plan jusqu'au dernier point. Une courbe est une courbe, un plan est un plan et les deux ne s'emboîtent pas. Il s'est avéré qu'ils s'emboîtaient.
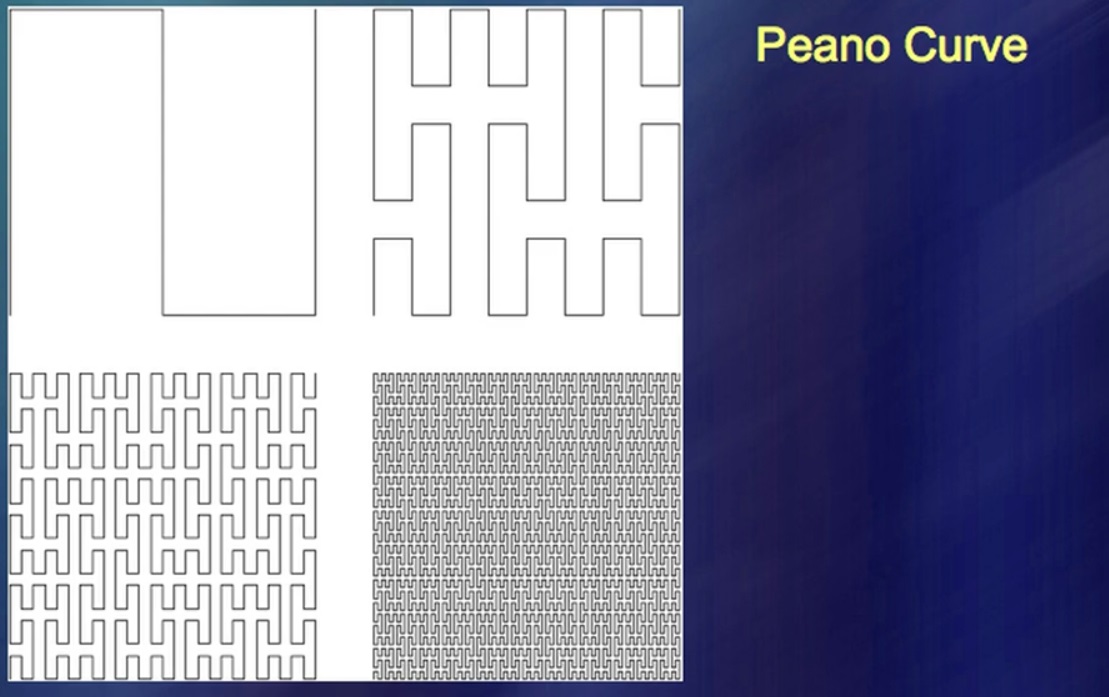
Un homme nommé Peano a identifié de telles courbes, et elles ont suscité un intérêt exceptionnel. Ils sont très importants et suscitent l'intérêt en grande partie parce qu'il y a eu une sorte de division des mathématiques en une mathématique qui est basée sur la réalité et une qui vient de la raison pure. Malheureusement, il m'est arrivé de prouver que ce qui est devenu connu grâce aux efforts de la raison pure, en fait, est connu depuis longtemps sous une forme différente. Ici, j'ai un système de ruisseaux en forme de courbes remplissant le plan.

En soi, c'est l'histoire. C'était entre 1875 et 1925, une période incroyable où les mathématiques s'apprêtaient à rompre avec le monde réel. Certains objets ont servi d'illustration de l'écart, depuis mon enfance et mes années d'étudiant, l'écart entre les mathématiques et la réalité visible. Cependant, j'ai réussi à les repenser, à les renverser et à décrire avec leur aide certains aspects de la complexité de la nature.
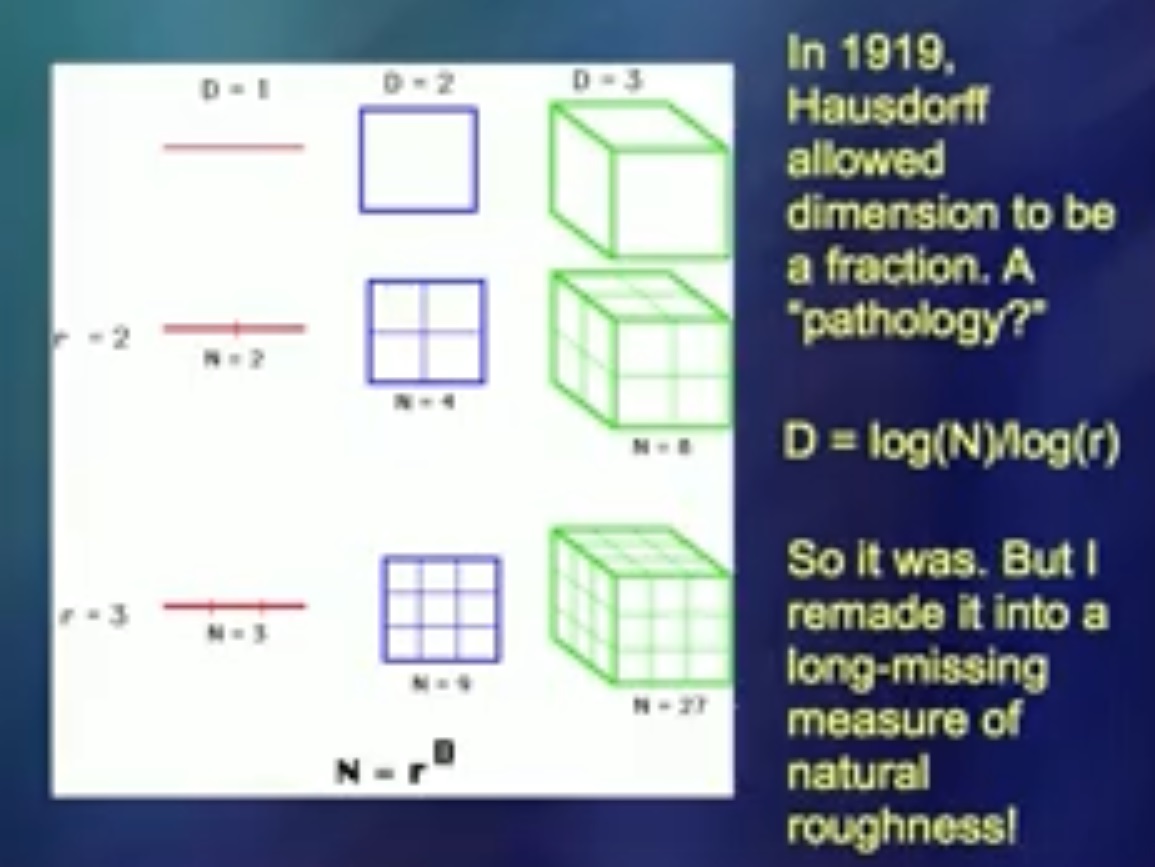
En 1919, un homme du nom de Hausdorff a identifié un nombre qui pourrait être considéré comme une blague mathématique. Mais j'ai trouvé que ce nombre est un bon outil pour mesurer le pli. Lorsque j'en ai parlé à mes collègues pour la première fois, ils ont dit: «Ne soyez pas stupide. C'est quelque chose ... »En fait, je ne faisais pas de bêtises.

Le grand artiste Hokusai le savait très bien. Au bas de l'image se trouvent des algues. Hokusai ne connaissait pas les mathématiques nécessaires: elles n'existaient tout simplement pas à l'époque. De plus, étant japonais, il n'avait [à l'époque] aucun contact avec l'Occident. Mais l'art a longtemps contenu des éléments fractals. Je peux en parler pendant longtemps.

La tour Eiffel a des éléments fractals. J'ai lu le livre d'Eiffel sur sa tour - l'étendue de sa compréhension est incroyable.
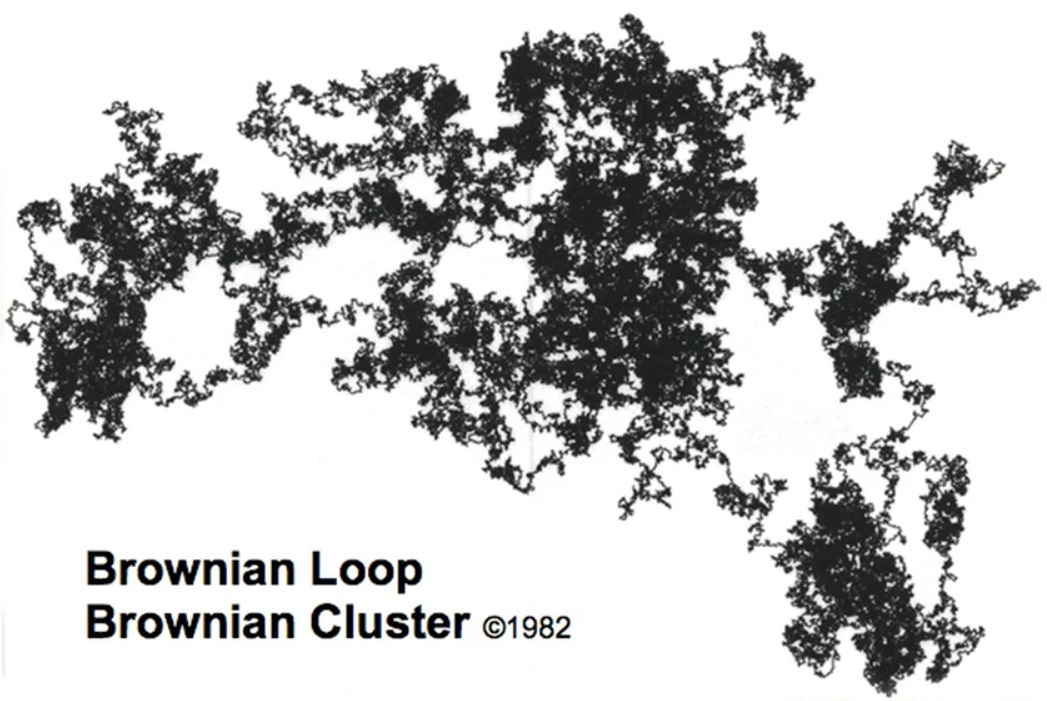
Voici un désordre dans un désordre. Boucle brownienne. Une fois, j'ai décidé que j'avais traversé une partie considérable de ma vie professionnelle, et tant de choses différentes m'occupaient que j'ai décidé qu'il était temps de me tester. Puis-je explorer un objet que tout le monde explore depuis longtemps et y trouver quelque chose de radicalement nouveau? J'ai commencé à étudier tout ce qui entre dans la catégorie du mouvement brownien. J'ai essayé différents angles, essayé différentes méthodes et je suis revenu à mon point de départ. Puis j'ai proposé à mon assistant: «Je ne vois rien ici. Pouvez-vous peindre? " Il l'a fait, c'est-à-dire qu'il a rempli tous les intérieurs. "Je me suis débrouillé…"

Mais j'ai crié: «Arrêtez! Arrêtez! Arrêtez! Compris: c'est une île. " Incroyable. Le mouvement brownien a un coude égal à deux. Je le mesure, il s'avère 1.33. Je mesure encore et encore. Mesures longues, grands mouvements browniens. Encore une fois: 1.33. Un problème mathématique se pose immédiatement: comment le prouver? Cela a pris 20 ans à mes amis. Trois avaient des preuves incomplètes. Ils ont uni leurs forces et ensemble, ils ont réussi à obtenir des preuves. En conséquence, ils ont reçu la célèbre médaille [Fields] des mathématiciens. Dans l'ensemble, les mathématiciens ont reçu trois médailles [Fields] pour avoir prouvé des faits que j'ai vus mais que je n'ai pas pu prouver.
Maintenant, les gens me demandent partout: «Comment tout cela a-t-il commencé? Comment vos études vous ont-elles conduit à des choses aussi inhabituelles? "
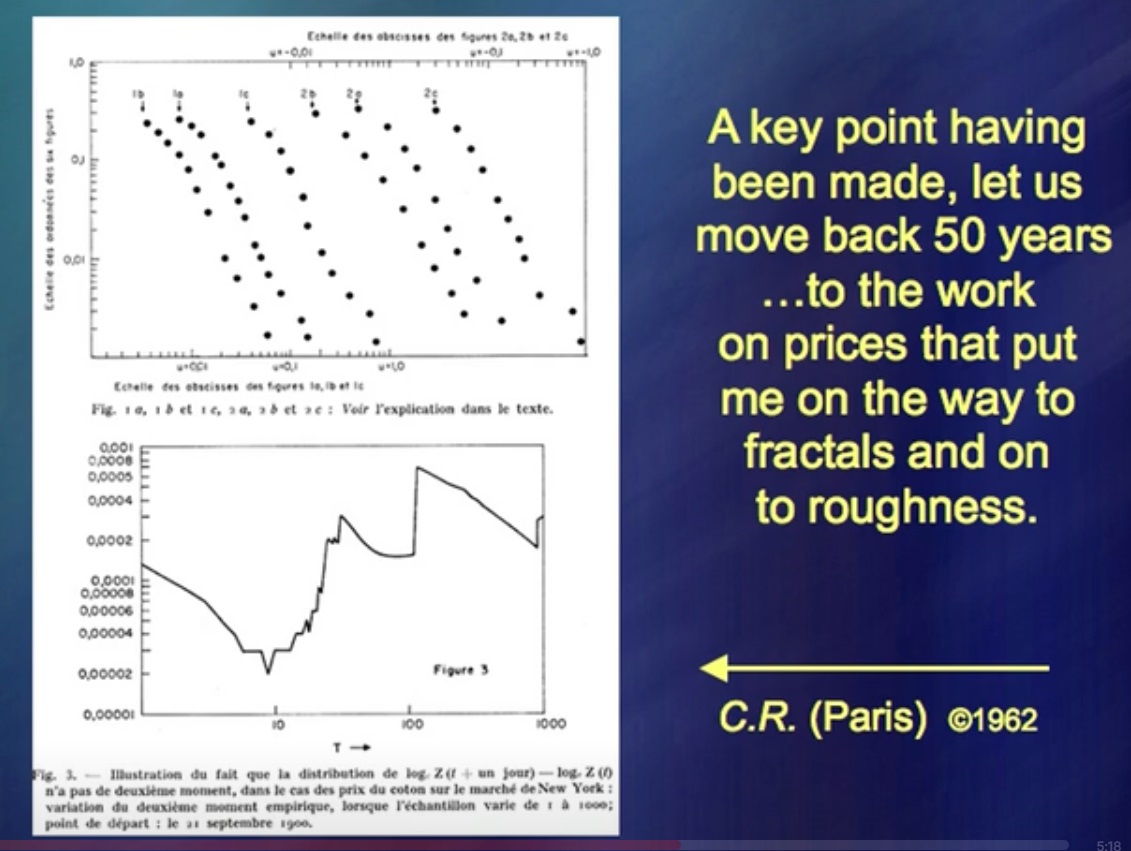
Qu'est-ce qui m'a permis d'être à la fois ingénieur mécanique, géographe, mathématicien, etc.? Curieusement, mais j'ai commencé par étudier les cours boursiers.

J'avais une théorie et j'en ai écrit des livres.
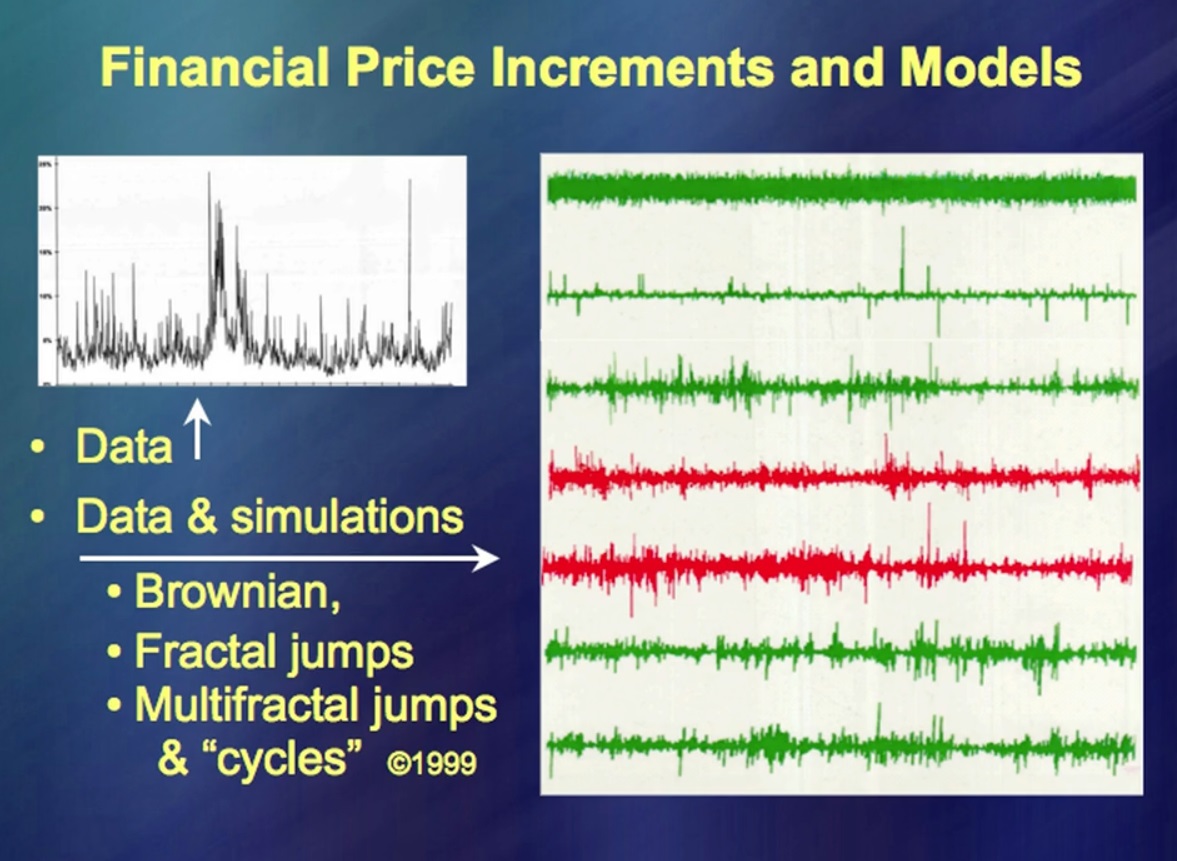
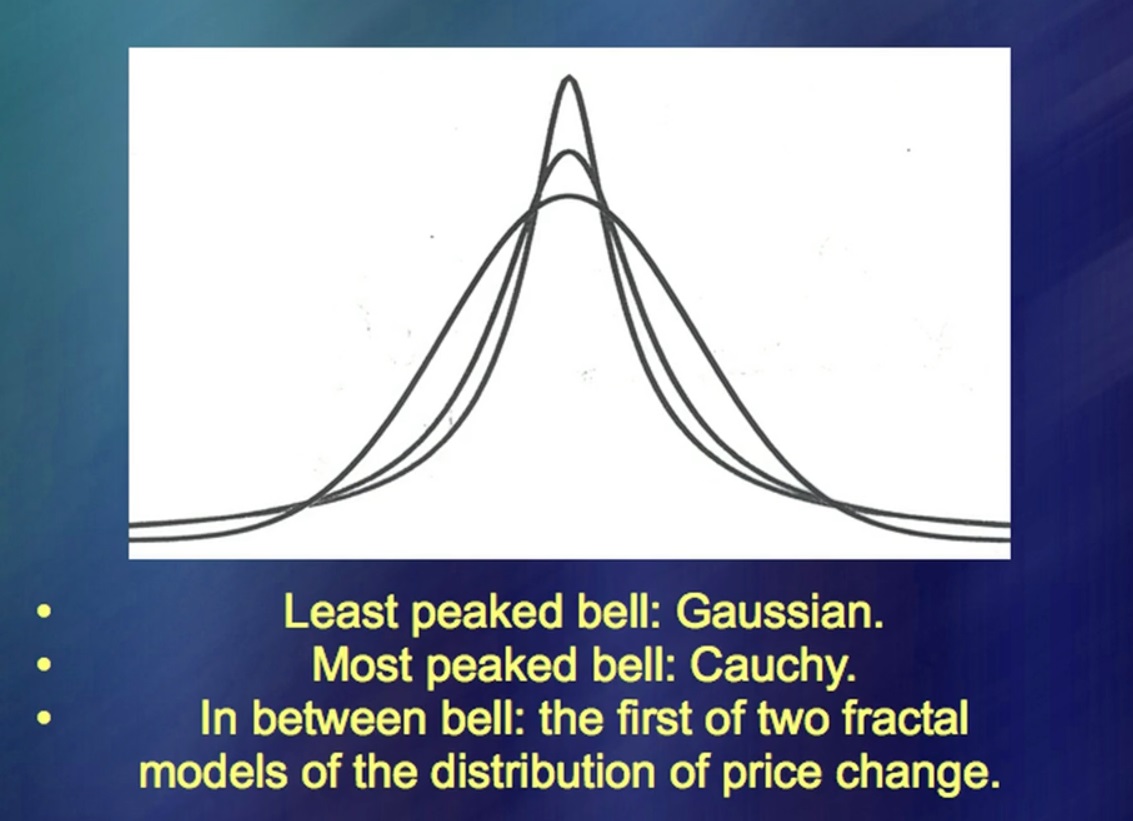
«Mouvements des prix des instruments financiers» À gauche, vous pouvez voir les données pendant une longue période, à droite, en haut - les données selon une théorie très, très à la mode. C'est extrêmement simple et vous pouvez écrire beaucoup de livres à ce sujet très rapidement. (Rires) Il existe des milliers de livres sur ce sujet. Maintenant, comparez avec les mouvements de prix réels. Et où sont-ils? Les lignes supplémentaires incluent des mouvements de prix réels ainsi qu'un petit faux de ma part. L'idée principale était que vous deviez être capable de faire ... Comment ça s'appelle? … Simulation des fluctuations de prix. Cela a très bien fonctionné il y a 50 ans.
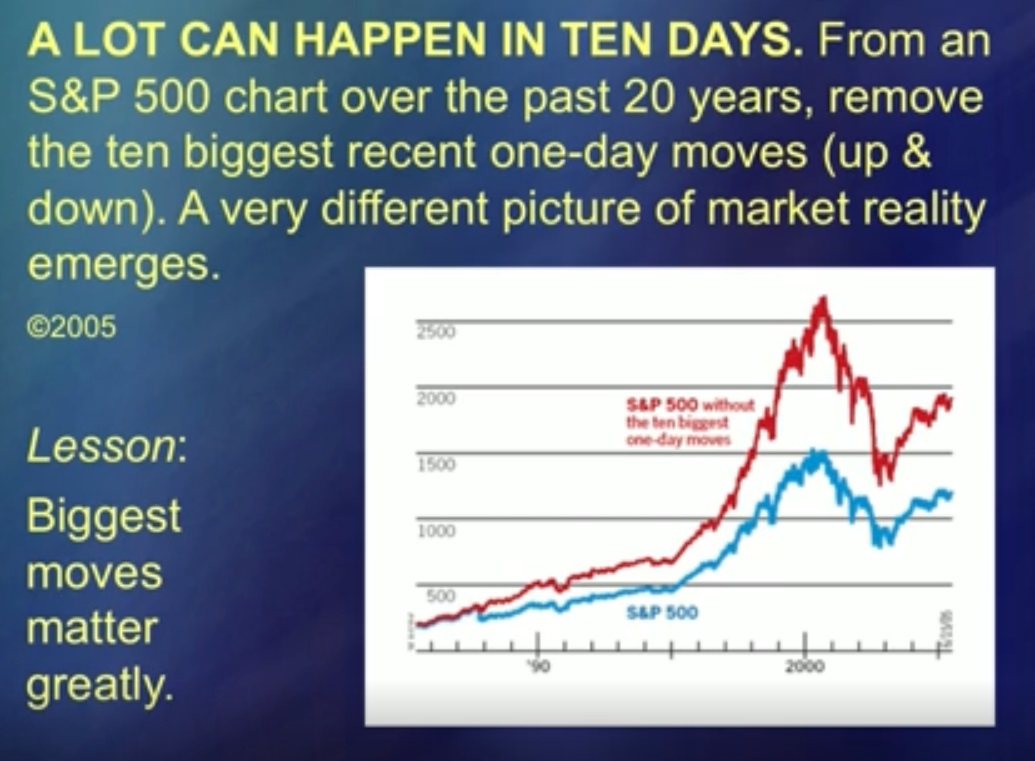
Pendant 50 ans, mon idée a été ridiculisée car elle aurait pu être plus facile. Mais maintenant, je vous le dis, ils ont commencé à m'écouter. (Rires) Ces deux courbes représentent des moyennes. Le bleu est le Standard and Poor's [S&P 500] et le rouge est le Standard and Poor's, dont les 5 plus grands pics de prix ont été soustraits. Le saut gâche certainement l'analyse, et dans de nombreuses études, il est considéré [non analytique] comme un cas particulier. «Incroyable coïncidence, intervention du Seigneur. Eh bien, une petite chose, vous pouvez simplement la mettre de côté. " Les interventions du Seigneur sur ce graphique, et il y en a exactement cinq, en fin de compte, sont aussi importantes que tout le reste. En d'autres termes, les interventions du Seigneur ne peuvent être mises de côté.
C'est un être, c'est l'objet même de l'analyse. Si vous traitez avec eux, vous pouvez également gérer les mouvements de prix. Mais je n'ai pas compris les sauts, alors vous pouvez analyser le soi-disant bruit autant que vous le souhaitez, mais cette analyse n'aura pas de sens. Ces courbes montrent l'impact.

Maintenant, je vais passer au dernier sujet - l'ensemble nommé d'après moi. D'une certaine manière, c'est l'histoire de ma vie. Mon adolescence s'est passée en France, occupée par l'Allemagne à l'époque. Puisque je pensais qu'à tout moment je ne serais peut-être pas, j'ai fait de grands rêves. Après la guerre, j'ai de nouveau rencontré mon oncle. Mon oncle était un mathématicien hors pair et il a dit: «Voici un problème pour vous. Il y a 25 ans, je ne pouvais pas le résoudre et personne ne pouvait le résoudre. Il s'agit de la construction d'un mathématicien nommé Gaston Julia et d'un autre nommé Pierre Fatou. Si vous pouvez trouver quelque chose de nouveau ici - n'importe quoi - considérez que votre carrière est assurée. " Très simple. J'ai commencé à étudier ce problème et, comme des milliers de ceux qui ont essayé de le faire avant moi, je n'ai rien obtenu.
Mais ensuite, les ordinateurs sont arrivés. Et j'ai décidé que je devais appliquer la puissance de calcul non pas à de nouveaux problèmes mathématiques - comme, par exemple, cette chose courbe: c'est un nouveau problème - mais à d'anciens problèmes. Et je suis passé des soi-disant nombres réels, c'est-à-dire des points sur une ligne droite aux nombres complexes, et ce sont des points sur un plan, c'est-à-dire ce qui est requis dans ce problème. Le résultat est un tel chiffre.

Celui-ci est d'une complexité exceptionnelle. L'équation y est cachée: z se transforme en z ^ 2 + c. Si simple et ennuyeux, si inintéressant. Maintenant, exécutons-le une, deux fois ... Deux fois, c'est assez. À propos d'un miracle! C'est ce qui apparaît. Je ne vais pas expliquer ces choses ici, mais il s'avère que c'est quoi et c'est quoi.


Des figures d'une telle complexité, d'une telle harmonie et d'une telle beauté sont obtenues à plusieurs reprises, encore et encore et encore. Ma principale découverte a été que ces îles ont plus ou moins la même forme que l'ensemble de la figure. Le résultat est un bijou baroque époustouflant.

Et toute cette formule courte, dans laquelle il y a tout - combien y a-t-il? - cinq icônes. Et c'est le résultat.

La couleur a été ajoutée pour deux raisons. Premièrement, parce que les chiffres sont si complexes qu'il est difficile de voir ce que signifient les chiffres. Et vous devez choisir une sorte de système pour les refléter dans l'avion. Par conséquent, j'ai pris comme principe de toujours représenter les personnages de différentes couleurs: une couleur signifie une chose, une autre signifie une autre, etc. C'est tellement dur.
En 1990, j'étais au Royaume-Uni, à Cambridge, où j'ai reçu un prix de l'université. Trois jours plus tard, un pilote, survolant le terrain, a vu cela.

D'où viendrait une telle chose? Bien sûr - des extraterrestres.
Un des journaux de Cambridge a publié un article sur cette "découverte", et le lendemain, il a reçu 5 000 lettres, qui disaient qu'il s'agissait de l'ensemble de Mandelbrot, juste très grand.

Laissez-moi finir. Cette image est obtenue grâce aux mathématiques pures. Des règles simples peuvent créer un miracle sans fond si elles sont répétées à l'infini.
Traduit par Namik Kasumov Révisé
par Ekaterina Tsvetkova

Apprenez en détail comment obtenir un métier recherché à partir de zéro ou passer au niveau supérieur en compétences et en salaire en suivant les cours en ligne payés de SkillFactory:
- Machine Learning (12 )
- Data Science (12 )
- (9 )
- «Python -» (9 )