Joshua Green et Andrew Lobb, ennuyés en quarantaine, ont compris comment prouver l'une des variantes du théorème de la cheville rectangulaire

Peut-on trouver toutes sortes de rectangles dans une boucle fermée?
À la mi-mars, les mathématiciens Joshua Green et Andrew Lobb se sont retrouvés dans une position similaire - enfermés entre quatre murs, essayant de s'adapter à l'épidémie croissante de coronavirus. Ils ont décidé de s'y attaquer en approfondissant leurs recherches.
«Je pense que la pandémie a été une sorte de catalyseur de ce processus», a déclaré Greene, professeur au Boston College. "Nous avons décidé qu'il serait préférable de mettre sur pied une sorte de travail conjoint qui puisse nous soutenir."
Un problème auquel les deux amis ont décidé de s'attaquer était une variante de la question géométrique restée sans réponse pendant plus de cent ans.
"Cette tâche est extrêmement simple à formuler et à comprendre, mais elle est très difficile à résoudre", - a déclaréElizabeth Denn de l'Université de Washington et Lee.
Tout commence par une boucle fermée - n'importe quel chemin courbe qui a le même début et la même fin. La tâche que Green et Lobb ont assumée soutient essentiellement que dans un tel chemin, il existe des ensembles de quatre points qui constituent les sommets d'un rectangle d'une proportion donnée.
Et bien que ce "problème de cheville rectangulaire" ressemble à une question que tout élève du secondaire avec une règle et une boussole peut gérer, il a résisté aux tentatives les plus persistantes des mathématiciens pendant de nombreuses décennies. Et lorsque Green et Lobb ont pris la relève, ils n'avaient aucune raison de s'attendre à autre chose.
Greene a déclaré que de tous les projets difficiles sur lesquels il a travaillé, "celui-ci était le moins prometteur à mon avis".
Mais la pandémie a augmenté et Green et Lobb, qui travaillent respectivement à l'Université de Durham en Angleterre et à l'Institut des sciences et technologies d'Okinawa, ont eu des conversations hebdomadaires avec Zoom et ont rapidement engendré plusieurs idées. Et puis, le 19 mai, lorsque de nombreuses régions du monde ont rouvert, ils ont publié leur décision .
Leur preuve finale, qui montre que l'on peut effectivement trouver des rectangles, porte ce problème à un tout autre niveau géométrique. Et là, cette question têtue cède très facilement.
"C'est assez bizarre", a déclaré Richard Schwartz de l'Université Brown. "Cette idée était parfaite pour cette tâche."
Repenser les rectangles
Le problème des chevilles rectangulaires est étroitement lié à la question posée par le mathématicien allemand Otto Töplitz en 1911. Il a prédit que sur n'importe quelle courbe fermée, vous pouvez trouver quatre points, reliant lesquels vous pouvez obtenir un carré. Sa question sur les «chevilles carrées» reste ouverte.
«C'est une tâche ancienne et frustrante qui ne peut en aucun cas être piratée», a déclaré Green.
Pour comprendre la complexité du problème, il est important de connaître les propriétés des courbes considérées dans le problème de la cheville carrée - ceci est également important pour la preuve de Green et Lobb.
Ce couple a résolu le problème des courbes fermées, à la fois «continues» et «lisses». La continuité signifie pas de pause. La douceur signifie la continuité et pas de coins. Vous êtes susceptible de dessiner une courbe lisse et continue si vous vous asseyez à votre bureau avec du papier et un crayon. Ils sont «plus faciles à travailler», a déclaré Green.
Les courbes continues lisses sont différentes des courbes simplement continues, mais non lisses, telles que celles impliquées dans la conjecture de Toeplitz des chevilles carrées. Une telle courbe peut avoir des coins - des points auxquels la courbe dévie soudainement et va dans une direction différente. Un excellent exemple d'une courbe avec de nombreux angles est la courbe fractale de Koch en forme de flocon de neige ., en fait, composé de quelques coins. Le flocon de neige de Koch et d'autres courbes similaires ne peuvent pas être analysés à l'aide de méthodes algébriques, ce qui les rend particulièrement difficiles à étudier.
"Certaines courbes continues [pas lisses] sont tout simplement dégoûtantes", a déclaré Denn.
Pourtant, le problème résolu par Green et Lobb appartient aux courbes lisses et donc continues. Et au lieu de déterminer s'il y a toujours quatre points sur de telles courbes qui forment un carré - pour les courbes continues lisses, ce problème a été résolu en 1929 - ils ont étudié autre chose: y a-t-il toujours quatre points sur de telles courbes qui forment un rectangle d'une donnée proportions, c'est-à-dire quel que soit le rapport hauteur / largeur. Pour un carré, ce rapport est de 1: 1, pour les téléviseurs haute définition - 16: 9.

La première percée majeure dans le problème des chevilles rectangulaires est apparue à la fin des années 1970 par Herbert Vaughn. Il a offert une nouvelle façon de regarder la géométrie des rectangles et a fourni plusieurs méthodes qui ont ensuite été utilisées par d'autres mathématiciens, y compris Green et Lobb.
«Tout le monde connaît cette preuve», a déclaré Green. "C'est presque folklorique, on apprend de telles choses en discutant de tout à table."
Plutôt que d'imaginer un rectangle comme quatre points connectés, Vaughn l'a envisagé comme deux paires de points en relation l'un avec l'autre.

Imaginez un rectangle avec des sommets ABCD. Dans celui-ci, la distance entre les points AC (sur la diagonale) est égale à la distance entre les points BD (sur l'autre diagonale). En outre, ces diagonales se coupent exactement au milieu.
Par conséquent, lorsque vous recherchez des rectangles sur une boucle fermée, vous pouvez rechercher des paires de points se trouvant aux extrémités des mêmes segments de ligne se croisant au milieu. Pour les trouver, il est important de trouver une manière systématique de les décrire.
Pour comprendre ce que cela signifie, commençons par quelque chose de plus simple. Prenez la droite numérique. Choisissons deux points dessus - disons les nombres 7 et 8 - et construisons-les comme un point sur le plan numérique (7, 8). Nous pouvons également construire des points qui sont une paire de nombres identiques (7, 7). Considérons maintenant toutes les paires de nombres possibles qui peuvent être trouvées sur la droite numérique (et il y en a beaucoup!). Si nous construisons toutes les paires de ces nombres, alors nous remplirons tout le plan numérique. Une autre manière d'exprimer cela est de dire que le plan numérique "paramètre", c'est-à-dire qu'il collecte toutes les paires de nombres sur la droite numérique d'une manière ordonnée.
Vaughn a fait quelque chose de similaire avec des paires de points sur une courbe fermée. Elle, comme la droite numérique, unidimensionnelle, ne se referme que sur elle-même. Il s'est rendu compte que si vous prenez des paires de points avec une courbe et que vous construisez une figure à partir d'eux (et peu importe lequel est la coordonnée x et lequel est le y), alors le plan ne fonctionnera pas. Au lieu de cela, vous obtenez une figure inattendue - une bande de Mobius , une surface bidimensionnelle avec un seul côté.

Et dans un sens, c'est assez logique. Pour comprendre pourquoi, sélectionnez une paire de points sur la courbe et nommez-les x et y. Maintenant, déplacez-vous de x vers y, en vous déplaçant le long d'une partie de la courbe, et simultanément - de y vers x, en vous déplaçant le long de l'opposé. Dans le processus, vous passerez par toutes les paires de points sur la courbe, en commençant et en terminant sur une paire non ordonnée (x, y). Mais cela vous ramènera au tout début - seule la séquence finale de points sera opposée à la séquence initiale. Une boucle de points désordonnés changeant d'orientation à l'opposé est l'essence même de la bande de Möbius.
Ce ruban donne aux mathématiciens un nouvel objet qui peut être analysé dans le cadre du problème de la cheville rectangulaire. Vaughn a utilisé ce fait pour prouver que sur n'importe quelle courbe, il y a au moins un ensemble de quatre points qui forment un carré.
Réponses en quatre dimensions
La preuve de Green et Lobb est basée sur le travail de Vaughn. Cependant, il combine également plusieurs découvertes supplémentaires, dont certaines sont relativement récentes. La preuve finale est comme un instrument précis, dont le résultat souhaité repose sur une combinaison d'idées soigneusement réfléchie.
L'un des premiers ingrédients principaux de leur preuve est venu en novembre 2019, lorsque l'étudiant au doctorat de l'Université de Princeton, Cole Hugelmeyer, a publié l' article.démontrant une nouvelle façon d'analyser la bande de Möbius utilisée par Vaughn. Il a utilisé un processus mathématique connu sous le nom d'imbrication, c'est-à-dire lorsque nous prenons un objet et le projetons sur un espace géométrique. En conséquence, Green et Lobb ont pris la technique de Hugelmeyer et l'ont transférée dans un autre espace géométrique. Mais pour comprendre ce qu'ils ont fait, vous devez d'abord comprendre ce qu'il a fait.
Voici un exemple simple d'imbrication.
Commençons par une ligne unidimensionnelle. Chaque point d'une ligne droite est défini par un seul nombre. Maintenant, nous allons intégrer cette ligne dans un espace bidimensionnel - c'est-à-dire que nous allons la dessiner sur un plan.
Après avoir intégré une ligne droite sur le plan xy, chaque point qu'il contient est déjà déterminé par deux nombres - les coordonnées x et y, qui décrivent exactement où se trouve le point sur le plan. Vous pouvez maintenant analyser la ligne à l'aide de techniques de géométrie 2D.
L'idée de Hugelmeier était de prendre quelque chose comme une bande de Möbius, mais de l'intégrer dans un espace à 4, où les propriétés de la géométrie à 4 dimensions vous permettront de prouver les résultats que vous souhaitez.
«Fondamentalement, vous avez une bande Mobius et vous devez attribuer quatre coordonnées à chaque point. Ce sera quelque chose comme l'adresse d'un point dans un espace à quatre dimensions », a déclaré Lobb.
Hugelmeyer a attribué ces adresses de telle manière qu'il était plus facile d'arriver à l'objectif principal, trouver des rectangles sur une courbe. Nous pouvons dire qu'il a attribué à chaque point de la courbe quelque chose comme une adresse postale - état, ville, nom de rue et numéro de maison.
Pour ce faire, il est parti d'un point précis de la bande de Mobius et a pris les deux points de la courbe fermée d'origine qu'elle a désignée. Puis il a trouvé le milieu du segment de droite reliant ces points et a déterminé ses coordonnées x et y. Nous avons obtenu les deux premières valeurs de l'adresse à quatre dimensions (état et ville).
Il a ensuite mesuré la distance entre les deux points d'origine sur la courbe. Cette longueur est devenue la troisième valeur de l'adresse à quatre dimensions (nom de rue). Enfin, il a calculé l'angle entre le segment de ligne reliant les deux points d'origine et l'axe des x. Cet angle est devenu la quatrième valeur de l'adresse à quatre dimensions (numéro de maison). Ces quatre valeurs vous disent tout sur une paire de points sur la courbe.

Cet exercice semble assez difficile, mais il a payé rapidement. Hugelmeyer a pris la bande Mobius attachée et l'a retournée. La bande Mobius tournée s'est déplacée par rapport à sa position d'origine et les deux copies de la bande se croisent. Puisque le virage a eu lieu dans un espace à quatre dimensions, la forme d'auto-intersection de la bande de Möbius est difficile à imaginer - mais elle est facile à décrire mathématiquement.
Cette intersection était d'une grande importance. Lorsque deux copies de la bande de Mobius sont superposées, deux paires de points peuvent être trouvées sur la courbe fermée d'origine, formant les quatre sommets du rectangle.
Pourquoi?
Tout d'abord, rappelez-vous qu'un rectangle peut être représenté comme deux paires de points avec un centre commun d'intersection de segments de même longueur les reliant. Ce sont ces informations qui sont codées dans les trois premières valeurs de l'adresse quadridimensionnelle affectée à chaque point de la bande de Möbius imbriquée.
Deuxièmement, dans un espace à quatre dimensions, vous pouvez déplier la bande de Möbius de manière à ne changer qu'une seule des coordonnées de chaque point dans son adresse à quatre dimensions - le numéro de maison change, mais la rue, la ville et l'état restent. Par exemple, rappelez-vous que si vous prenez une brique, que vous la positionnez devant vous, puis que vous la déplacez vers la droite, seule sa coordonnée x changera, mais pas y ou z.
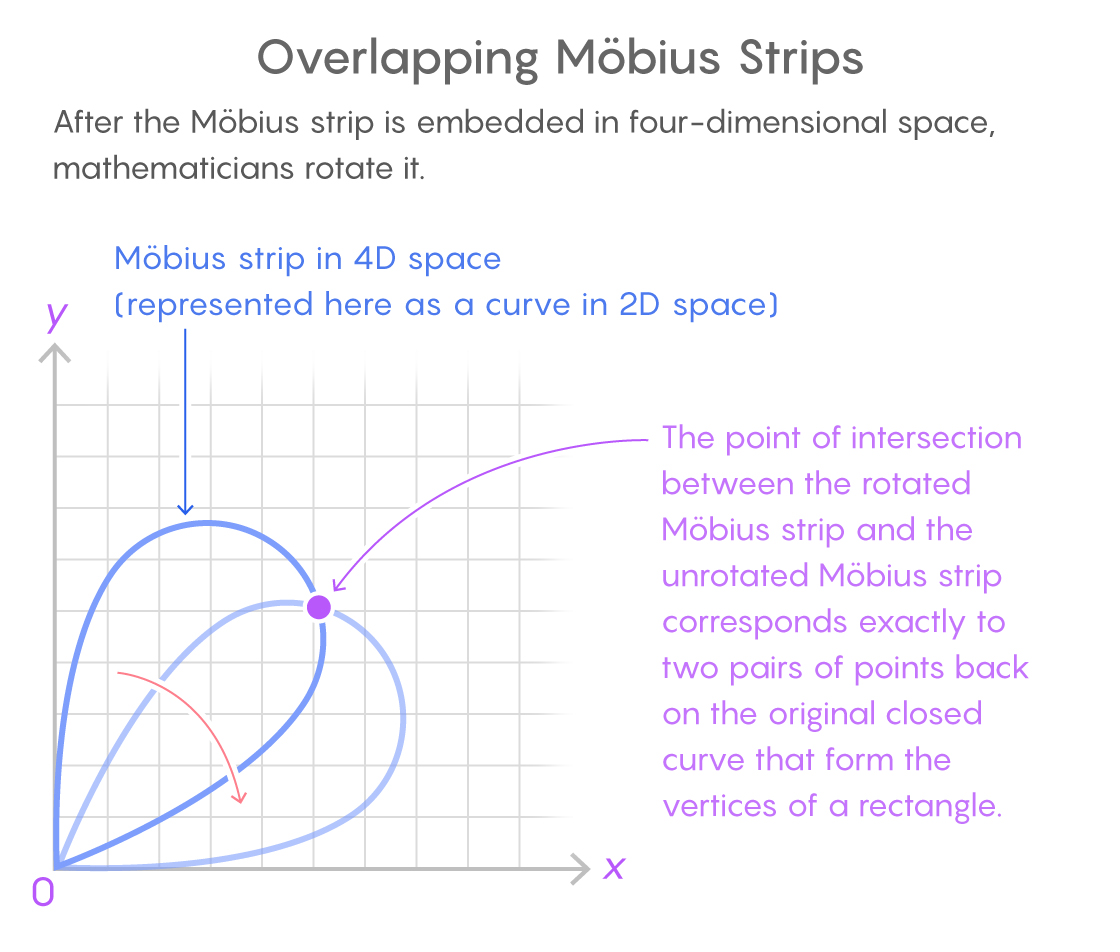
La bande de Möbius dans l'espace quadridimensionnel est ici indiquée par une courbe bidimensionnelle. Le point d'intersection des deux copies correspond à deux paires de points sur la courbe fermée d'origine qui forment un rectangle.
Hugelmeyer a expliqué comment faire pivoter la bande de Mobius dans un espace à quatre dimensions afin que les deux coordonnées qui indiquent le milieu des lignes reliant les paires ne changent pas - tout comme les coordonnées qui indiquent la distance entre les paires de points. Sa rotation n'a changé que la dernière coordonnée - contenant des informations sur l'angle auquel se trouve le segment reliant les points.
En conséquence, l'intersection de la copie tournée de la bande de Möbius et de son original correspondait exactement à deux paires de points situés sur une courbe fermée, ayant un centre commun (intersections des segments les reliant) et situés à la même distance l'un de l'autre. Autrement dit, cette intersection correspond aux quatre sommets du rectangle sur la courbe.
La stratégie consistant à utiliser l'intersection de deux espaces pour trouver les bons points a longtemps été utilisée dans les travaux sur les problèmes des chevilles carrées et rectangulaires.
"A l'intersection de ces espaces se trouve celui souhaité", a déclaré Denn. "Beaucoup de preuves de l'histoire des chevilles carrées ont cette idée."
Hugelmeyer a utilisé une stratégie d'intersection dans un environnement à quatre dimensions et en a obtenu plus que quiconque avant lui. La bande Mobius peut être tournée de n'importe quel angle de 0 ° à 360 °, et il a prouvé qu'un tiers de toutes ces rotations aboutit à l'intersection de l'original et de la copie pivotée. Cela équivaut à indiquer que vous pouvez trouver des rectangles sur une courbe fermée avec un tiers de tous les rapports hauteur / largeur possibles.
«Nous remercions Cole d'avoir pensé à mettre une bande Mobius dans l'espace 4D et à utiliser des techniques 4D», a déclaré Green.
Dans le même temps, le résultat de Hugelmeier s'est avéré provocateur: si l'espace à quatre dimensions est si utile pour travailler avec ce problème, pourquoi l'a-t-il été pour seulement un tiers de tous les rectangles?
"Après tout, il doit y avoir un moyen d'obtenir les deux tiers restants", a déclaré Green. - Mais comment?"
Approche symplectique
Green et Lobb s'intéressaient au problème des chevilles rectangulaires avant même que la pandémie ne les renvoie chez eux. En février, Lobb a organisé une conférence à l'Okinawa Institute of Science and Technology , à laquelle Green a également participé. Le couple a passé quelques jours à parler de cette tâche. Après cela, ils en ont discuté pendant une autre semaine, tout en voyant les sites touristiques de Tokyo.
«Nous n'avons pas arrêté de discuter de cette question», a déclaré Lobb. «Nous sommes allés dans des restaurants, des cafés, des musées et de temps en temps nous avons pensé à cela.
Ils ont continué leurs discussions même après avoir été enfermés chez eux. Ils espéraient prouver que toute rotation de la bande de Mobius donnerait un point d'intersection - ce qui équivaut à trouver des rectangles de n'importe quelle proportion.
À la mi-avril, ils ont formé une stratégie. Cela signifiait intégrer la bande dans un type spécial d'espace à quatre dimensions. L'imbrication régulière implique que vous placez l'objet souhaité de quelque manière que ce soit. Imaginez de combien de façons vous pouvez intégrer une courbe fermée unidimensionnelle dans un plan bidimensionnel - leur nombre est infini, car il existe une infinité de façons de placer un fil lié en boucle sur une table.
Mais disons que la surface bidimensionnelle dans laquelle vous imbriquez la boucle a sa propre structure. Imaginez, par exemple, une carte avec des flèches (ou vecteurs) nous indiquant dans quelle direction et à quelle vitesse le vent souffle à la surface de la Terre. Vous avez maintenant une surface 2D avec des informations supplémentaires, ou une structure, à chaque point.
Ensuite, vous pouvez introduire des restrictions - un appel d'offres unidimensionnel doit être placé sur la carte afin qu'il suive toujours les directions des flèches sur la carte.
«Vous limitez les choses pour que la courbe suive ces vecteurs», a déclaré Schwartz. Et maintenant, vous avez moins de façons de placer la courbe.

D'autres espaces géométriques peuvent imposer des contraintes différentes. Important pour le travail de Green et Lobb était le soi-disant. espace symplectique .
Ce concept géométrique est apparu pour la première fois au 19ème siècle lors de l'étude de systèmes physiques tels que les planètes en orbite. La position d'une planète se déplaçant dans un espace tridimensionnel est déterminée par trois coordonnées. Mais, comme l'a observé le mathématicien irlandais William Rowan Hamilton, à chaque point de la trajectoire de mouvement de la planète, vous pouvez également placer un vecteur indiquant son élan.
Dans les années 1980, le mathématicien soviétique et russe Vladimir Igorevich Arnold a développé l'étude de la géométrie symplectique . Il s'est rendu compte que les espaces géométriques d'une structure symplectique, lorsqu'ils sont tournés, se croisent plus souvent que les espaces qui n'ont pas une telle structure.
C'était parfait pour Green et Lobb, car ils voulaient résoudre le problème de la cheville rectangulaire pour toutes les proportions, prouvant qu'une copie tournée d'une bande de Mobius paramétrable se coupe également fréquemment. Ils ont donc commencé à essayer d'incorporer une bande de Möbius à deux dimensions dans un espace symplectique à quatre dimensions. «Une idée radicalement nouvelle était d'aborder ce problème du point de vue de la géométrie symplectique», a déclaré Green. "Et cela a tout changé."
À la fin du mois d'avril, Green et Lobb ont déterminé qu'il était possible d'intégrer une bande de Mobius dans un espace symplectique à quatre dimensions afin qu'elle s'aligne sur sa structure. Après cela, ils pourraient commencer à utiliser des outils de géométrie symplectique, dont beaucoup sont directement liés à la question des auto-intersections.
«Si la bande de Möbius peut être amenée à suivre des règles symplectiques, certains des théorèmes symplectiques peuvent être utilisés», a déclaré Lobb.
Green et Lobb étaient convaincus qu'ils pourraient améliorer le résultat de Hugelmeyer - c'est-à-dire prouver que l'intersection ne se produit pas seulement à un tiers de tous les virages. Cela signifiera qu'à partir des points de la courbe, il sera possible de faire des rectangles avec plus d'un tiers de toutes les proportions possibles.
«Lorsque nous avons eu cette idée, il est devenu clair que quelque chose allait se passer», a déclaré Lobb.
Cependant, leurs résultats se sont révélés plus généraux et sont apparus beaucoup plus rapidement que prévu. Tout cela grâce à un objet mathématique étrange - la bouteille de Klein , qui dans le contexte de la géométrie symplectique a une propriété importante.
Raccord de bouteille Klein
La bouteille Klein est une surface bidimensionnelle qui ressemble à une cruche moderniste. Comme la bande Mobius, elle n'a qu'une seule surface et peut être réalisée en collant deux bandes Mobius. Toute bouteille de Klein que vous pouvez collecter et placer sur votre bureau (comme le font de nombreux mathématiciens) se croise. Il est impossible de mettre une bouteille de Klein dans un espace tridimensionnel pour qu'elle ne se croise pas.
«La bouteille de Klein doit être une surface, mais sa poignée doit traverser la bouteille pour aller de l'extérieur vers l'intérieur», a déclaré Schwartz.
Toutefois, ce n'est pas necessairement le cas. La bouteille de Klein peut être imbriquée dans l'espace 4D afin qu'elle ne se coupe pas. La quatrième dimension offre une marge de manœuvre et la bouteille de Klein peut se contourner. Cela peut être comparé à la façon dont si deux personnes marchent l'une vers l'autre sur une ligne unidimensionnelle, elles ne peuvent pas éviter une collision, mais si elles marchent sur un sol en deux dimensions, elles peuvent facilement se détourner.

En mai, Green et Lobb ont rappelé un fait sur la bouteille de Klein - elle ne peut pas être intégrée dans un espace symplectique à quatre dimensions afin qu'elle ne se recoupe pas [d'après les travaux d' un autre mathématicien russe, Vsevolod Viktorovich Shevchishinconcernant l'enrobage lagrangien de la bouteille de Klein dans un espace quadridimensionnel / env. trad.]. En d'autres termes, il n'y a pas de bouteille de Klein sans auto-intersection qui satisfasse toutes les exigences d'un espace symplectique. Ce fait est devenu la clé de la preuve. «C'était une baguette magique,» dit Green.
Et c'est pourquoi. Green et Lobb ont déjà montré qu'il était possible d'intégrer une bande de Mobius dans un espace symplectique à quatre dimensions afin qu'elle réponde à ses exigences. Ils avaient seulement besoin de savoir si chaque tour de la bande Mobius croise la copie originale.
Cependant, deux bandes Mobius qui se croisent sont équivalentes à une bouteille de Klein, qui se croise dans un tel espace. Et si vous faites pivoter la bande Mobius pour que la copie pivotée ne se croise pas avec l'original, vous obtenez une bouteille Klein qui ne se croise pas. Mais une telle bouteille de Klein ne peut pas exister dans un espace symplectique à quatre dimensions. Par conséquent, toute rotation possible de la bande de Möbius imbriquée doit également se croiser - c'est-à-dire que sur chaque courbe lisse fermée, quatre points peuvent être trouvés qui forment un rectangle de toutes proportions.
La fin de la preuve frappe le lecteur comme une avalanche.
«C'est d'abord mis en place, mis en place, mis en place, puis grogner, et la preuve est prête», a déclaré Denn.
La preuve de Green et Lobb est un bon exemple de la façon dont la résolution d'un problème repose souvent sur la recherche du bon point de vue. Des générations de mathématiciens ont été incapables de s'attaquer à cette version du problème de la cheville rectangulaire parce qu'ils ont essayé de le résoudre dans des conditions géométriques plus traditionnelles. Lorsque Green et Lobb ont introduit le problème dans le monde symplectique, il a été facilement résolu.
«Ces problèmes, qui sont apparus dans les années 1910 et 1920, n'avaient pas de plate-forme appropriée pour y réfléchir», a déclaré Green. "Et maintenant nous commençons à comprendre qu'ils sont, en fait, des incarnations cachées du phénomène de symplecticité."