Le modèle mathématique du phénomène postule que tous les processus se déroulent dans un espace-temps à 4 dimensions, dans lequel les phénomènes SRT découlent de la préservation de l'intervalle des événements lors de la transformation de la rotation du système de coordonnées. On ne peut guère nier que la réalité est en quelque sorte tiraillée sur les constructions mathématiques. De plus, le fait que les nombres imaginaires, en réalité inimaginables, y jouent un rôle presque entièrement important, ne diminue en rien le succès de la science. Même E. Mach a dit que les explications sont superflues si les phénomènes observés sont bien décrits par des formules. Et ne discutons pas avec cette empirio-critique.
Les mathématiciens inventent des abstractions et les essayent à la réalité. D'où la singularité, les trous de ver et autres choses exotiques. Ou peut-être vaut-il la peine de fantasmer , par exemple, sur ce qui changerait dans nos idées sur le monde si la cause de la contraction de Lorentz était un mécanisme physique hypothétiquement supposé. Pourquoi pas?
1 La cause physique de la contraction de Lorentz
Tout d'abord, j'exprimerai la maxime apparemment évidente selon laquelle les particules, les atomes, les molécules interagissent les uns avec les autres par le biais de champs physiques . On peut bien sûr dire qu'ils échangent des particules quantiques, mais on joue maintenant sur le terrain de la théorie relativiste, donc pour l'instant on oubliera les quanta. Donc, la première hypothèse fantastique est que c'est précisément en raison de l'équilibre mutuel des effets de champ que les particules sont ajoutées à une certaine configuration et forment des corps . Si une particule dévie de la position d'équilibre, alors une perturbation de champ s'en échappera, ce qui déplacera le reste des particules, ce qui, à son tour, provoquera un effet de champ inverse de leur part sur cette particule.
Et la deuxième hypothèse est quela perturbation du champ se propage dans un certain espace commun avec une certaine vitesse . Et la nature fantastique de cette hypothèse est que, selon la science, le champ existe par lui-même dans l'espace-temps à 4 dimensions (P-W) et ne s'étend sur rien. En général, c'est difficile en science ... Nous supposerons que les champs se répandent et existent dans un seul espace tridimensionnel - dans lequel nous sommes, la Terre et les étoiles. Il semble que cela va de soi et qui ne sait pas, mais voyons ce qui se passe. Ceux qui ne sont pas intéressés à se soucier des formules peuvent se limiter à lire uniquement le texte sélectionné.
Donc, nous sommes d' accord qu'il y a un temps d'interaction entre les particules, qui se compose de l'heure d'arrivée de l'indignation envers eux et de l'heure de retour de la réponse de leur part. En conséquence, la configuration précédente du corps sera progressivement rétablie. Fig.1 Influences du champ qui déterminent la position de la particule
Pour tout point du corps, il est possible de distinguer des groupes de points avec lesquels il aura des temps d'interaction égaux et que nous appellerons isochrones avec ce point. La situation est reflétée sur la figure 1. Naturellement, au repos, la sphère de tout rayon de repos R autour d'un point est le lieu des points (GMT) isochrone avec lui.
Notez que le mouvement d'une particule à chaque instant est déterminé par la somme des forces résultantes qui sont appliquées simultanément à partir de la totalité de tous les groupes de particules isochrones avec elle... Essayons de découvrir comment la surface du GMT, formée par un ensemble de points 2, 3, etc., va changer lorsque le corps bouge. avec les mêmes temps d'interaction avec le point 1, qui peut ne plus être une sphère.
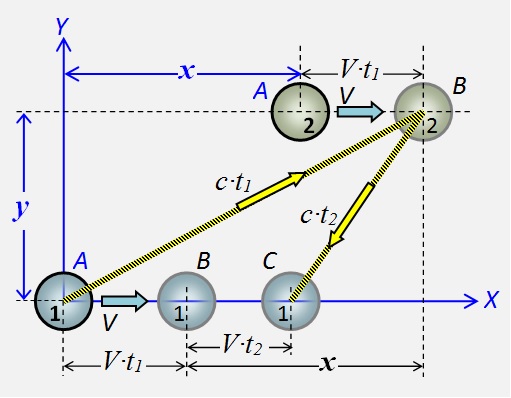Let points du corps 1 et 2 sont fixées mutuellement et se déplaçant de manière synchrone avec la vitesse la droite V . Quand un point est à l'origine, le champ de perturbation est envoyée au point 2. Le consentement mutuel des points marqués par la lettre A . Fig.2 Schéma des interactions de champ des points du corps - aller-retour
Lorsque la perturbation atteint le point 2, elle parcourra la distance V ∙ t 1 . Les positions marquées points avec la lettre B . Pendant le temps où la perturbation revient du point 2 au point 1, le point 2 couvrira la distanceV ∙ t 2 . Leur nouvelle position est marquée par la C .
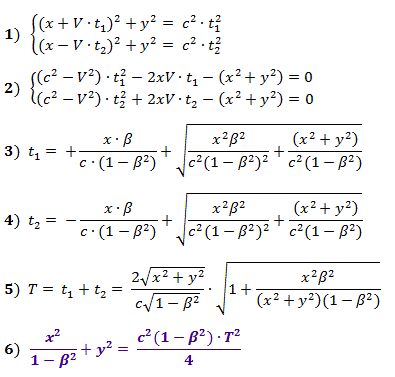Les formules (1), selon le théorème de Pythagore, décrivent les distances dans la figure 2, et les obtenues à partir d'elles (2) sont des équations pour calculer les temps t 1 et t 2 , dont les valeurs sont données par les formules (3) et (4) pour les valeurs positives des racines, où β = V / c .
La formule (5) donne la valeur du temps d'interaction entre l'envoi d'une perturbation et la réception d'une réponse.
À partir de (5), nous obtenons l'équation (6) pour les coordonnées x et y du lieu géométrique des points isochrones avec lesquels le temps d'interaction du point 1 est le même.
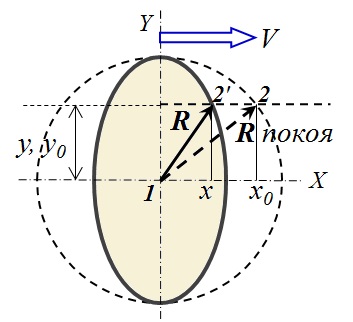La formule (6) décrit l'ellipsoïde représenté sur la figure 3, comprimé le long de la direction du mouvement (le long de l'axe X) de √ (1 - β 2 ) fois, c'est-à-dire selon la formule de Lorentz. Le point 2 sur la surface de la sphère au repos, en se déplaçant, se déplacera en position 2 ' . Dans ce cas, les points matériels qui étaient isochrones avec le point 1 au repos resteront isochrones avec lui pendant le mouvement . Fig.3
Ainsi, lors d'un déplacement, un objet matériel est compressé selon Lorentz précisément parce que «l'image» même des champs physiques est compressée, ce qui garantit son intégrité dans l'espace .
Puisque la contraction de Lorentz est la même pour tous les points isochrones entourant chaque point de l'objet, alors tout l'objet en mouvement se contractera également proportionnellement le long de l'axe de mouvement.
2. Dérivation de la formule de dilatation du temps
Déterminons le temps d'interaction lorsque l'objet est en mouvement par rapport au temps d'interaction au repos.
Les formules (7) relient les coordonnées de points pendant le mouvement à leurs coordonnées au repos conformément à l'
équation (6). La formule (8) calcule le temps d'interaction au repos. Les formules (9) et (10) ont été obtenues à partir de la formule (6) en y substituant les valeurs des coordonnées x et y et R de repos des formules (7). La formule (11) équivaut à (10). La formule (12), obtenue à partir de (11) en y substituant le côté gauche de la formule (8), relie les temps d'interaction au repos et pendant le mouvement. Dans la forme traditionnelle, cela se reflète dans la formule (13), où T 0 est l'intervalle de temps entre les événements dans un objet au repos, etT est l'intervalle de temps entre les mêmes événements dans un corps en mouvement.
Ainsi, les temps d'interaction de tous les points d'un objet en mouvement augmentent dans la même proportion selon Lorentz par rapport au temps d'interaction au repos. En conséquence, en général, tous les processus dans un objet en mouvement ralentissent en fait de la même manière .
La raison du ralentissement du temps est facile à comprendre si l'on tient compte du fait que la perturbation du champ de l'arrière des particules en interaction devra rattraper celle de l'avant dans le sens du mouvement . Lorsque la vitesse du corps est presque égale à la vitesse de la lumière, il faudra beaucoup de temps pour rattraper son retard, et si la vitesse du corps est égale à la vitesse de la lumière, il ne rattrapera jamais. Tous les changements dans le corps s'arrêteront et le temps semblera s'arrêter.
3.Explication du phénomène de la constance de la vitesse de la lumière, etc.
Faisons une expérience de pensée. Laissez une impulsion de lumière être émise par la dernière voiture du train, qui est reçue dans sa voiture de tête. Il faut mesurer le temps T 0 que passera la lumière au passage d'un train de longueur connue L 0 dans son propre système. Dans la preuve, nous utiliserons les hypothèses sur l'homogénéité et l'isotropie de l'espace, en particulier, nous supposerons les mêmes résultats de mesure pour les première et deuxième moitiés du train, ainsi que pour les directions avant et arrière. Mais, à proprement parler, ces hypothèses ne sont valables que dans le lieu et l'heure de l'expérience.
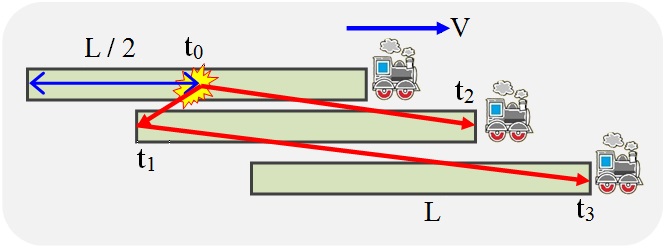
Fig. 4. Expérience de réflexion pour déterminer la vitesse de la lumière dans un train en mouvement
Pour synchroniser le moment de l'envoi d'un signal de la dernière voiture du train et le début du compteur de temps dans sa voiture avant, nous utilisons une impulsion de lumière de départ du milieu du train aux deux extrémités.
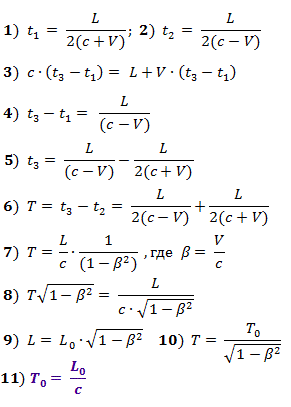
Lorsque le signal de départ du milieu du train atteint sa queue (temps t 1 ), une impulsion lumineuse sera envoyée. Lorsque le signal de départ atteint la tête du train (temps t 2 ), le compte à rebours commencera jusqu'à l'arrivée de l'impulsion envoyée.
Lorsque la lumière se déplace vers la queue, sa vitesse est ajoutée à la vitesse du train, quand à la tête, la vitesse du train est soustraite. On obtient les relations données ci-dessous dans les formules (1) - (6).
Le temps T = t 3 - t 2 est l'intervalle de temps, qui,selon l'observateur sur le train , il sépare les événements du moment d'envoi du signal de la fin du train (à partir du moment de la réception du signal de départ là-bas) et du moment de sa réception en tête du train.
De (6) nous obtenons la formule (7), que nous transformons en la forme (8). De plus, nous tiendrons compte du fait que toutes les grandeurs L , T et t sont ici mesurées dans le référentiel d'un observateur extérieur dans l'espace où se déroule l'expérience de pensée. Mais quand un objet se déplace dans l'espace, sa longueur, comme le montre le chapitre 1 , subit en fait une contraction de Lorentz, et les temps des événements, comme prouvé au chapitre 2, ralentissez en fait du même nombre de fois, c.-à-d. procéder plus longtemps qu'au repos, ce qui se reflète dans les formules (9) et (10). En remplaçant ces rapports dans la formule (8) pour l'intervalle T - le temps de trajet de la lumière de la queue à la tête du train, nous obtenons la relation (11).
Mais quelle relation ces T 0 et L 0 au repos ont-ils avec leur temps et leur durée propres pour les mêmes événements, mesurés dans le référentiel inertiel (IRF) associé à un train en mouvement? De toute évidence, ils sont leurs égaux . Le fait est que le temps et la durée sont exprimés numériquement par leur relation avec les normes. En conséquence, les mesures des coordonnées temporelles et spatiales de quelque chose fait au repos seront numériquementsont égales aux mesures de la même chose, effectuées dans un ISO en mouvement, car lors du déplacement, les valeurs des mesures et des normes changeront proportionnellement.
La question est de savoir comment ils changent exactement lorsqu'ils se déplacent dans l'espace. Une expérience de pensée avec un train prouve qu'ils évoluent de telle sorte que la valeur numérique de la vitesse de la lumière mesurée en IFR reste égale à la valeur de sa vitesse dans l'espace . C'est précisément ce qui n'était pas a priori une preuve évidente et requise.
On voit que le «postulat de la constance de la vitesse de la lumière» est dérivé du seul fait de la contraction de Lorentz, qui est mathématiquement dérivée de la dépendance de l'emplacement de la matière matérielle sur la vitesse de propagation et la configuration des champs physiques dans l'espace .
Pour compléter le tableau, nous définissons également la vitesse de la lumière à travers le mouvement du train, par exemple, entre les parois du wagon à une distance S 0 les unes des autres. Pour ce faire, nous mesurons le temps de mouvement de l'impulsion lumineuse ( 2 · t 0 ) d'avant en arrière. Au vu de la symétrie évidente du «là» et du «dos», nous ne considérerons que «là». Dans le système d'un observateur extérieur, le mouvement dans l'espace se produit comme le montre la figure 5.
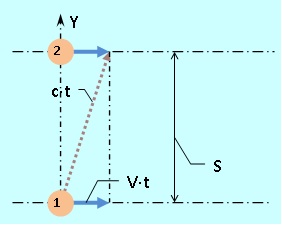On a donc (c · t) 2 = S 2 + (V · t) 2 , d'où on obtient t = S / (c · √ (1 - β²)) , où β = V / c .
Dans le système de train, le temps propre écoulé t 0lié au temps passé dans l'espace par la relation t = t 0 / (√ (1 - β²)) . En substituant cette expression à la formule de t dans l'espace, nous obtenons t 0 = S / c .
Fig. 5. Expérience de pensée pour déterminer la vitesse de la lumière dans un train en mouvement /
Dans le système du train pour le même t 0, nous avons la relation t 0 = S 0 / c 0 . Mais puisque les dimensions transversales ne changent pas pendant le mouvement, c'est-à-dire S = S 0 , on obtient que c 0 = c .
Je suppose qu'il n'est pas nécessaire de prouver la constance de la vitesse mesurée de la lumière pour une orientation arbitraire du faisceau, ce qui ne ferait qu'ajouter une complexité inutile. Compte tenu de l'invariance prouvée de la vitesse de la lumière, il est facile de dériver les transformations de Lorentz (L), et sans aucun recours aux équations de Maxwell ou à l'espace mathématiquement abstrait de Minkowski.
4. Dérivation des transformations de Lorentz
L'événement consiste en l'arrivée d'une impulsion lumineuse au point " E ",
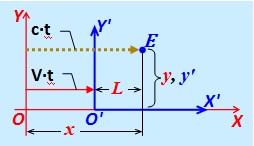située en coordonnées inchangées x ' et y' dans le repère {X ', Y'}, se déplaçant à une vitesse V relative à l'IFR fixe {X, Y}, envoyée au moment où les points O et O 'des deux CO coïncidaient. Fig. 6.
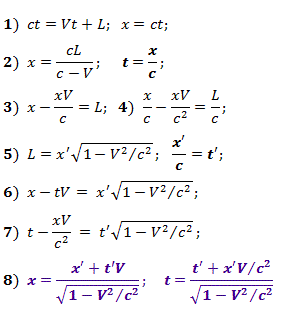Dans sa propre longueur CO {X ', Y'} L , mesurée en CO {X, Y}, la coordonnée x ' correspondra . Pour l'événement, le système d'équations (1) est valide, résolvant ce que nous obtenons (2), puis (3) et (4).
Puisque les longueurs des corps en mouvement sont compressées selon Lorentz, et que la vitesse de la lumière, comme prouvé dans Ch.3 , est la même dans n'importe quel FR, alors pour x 'etLes relations t ' dans {X', Y '} (5) sont valides. En substituant les relations de (5) à (3), nous obtenons (6), et en les substituant en (4), nous obtenons (7). En vertu de la relativité du mouvement, nous pouvons considérer le système mobile {X, Y}, mais alors dans (6) et (7) il est nécessaire de remplacer les variables non ombrées par les variables ombrées, et la vitesse V doit être prise avec le signe opposé, ou simplement résoudre le système par rapport à x et t .
En conséquence, nous obtenons des expressions (8) pour la forme canonique des transformations de Lorentz des coordonnées et du temps des événements dans différents IFR.
Lorsqu'on utilise PL comme méthode mathématique purement formelle, le mécanisme physique des phénomènes SRT reste non manifesté. Par conséquent, dans mes articles précédents sur l' effet Doppler relativisteetles aberrations lumineuses , ainsi que les lois de réflexion d'un miroir incliné en mouvement , les SL n'ont en principe pas été utilisées pour démontrer les raisons physiques de ces phénomènes.
5. Justification du principe de relativité et limites de son applicabilité
Notez que si au repos dans le diagramme de la figure 1 la perturbation du point 1 au GMT des points isochrones avec lui est venu simultanément, alors pendant le mouvement, dans le diagramme de la figure 2, cela n'est plus rempli. A chaque point de ce GMT, la réponse à la perturbation sera créée à des moments différents, mais ils convergeront au point 1 simultanément . La question est: le résultat sera-t-il le même qu'au repos?
Il a été prouvé ci - dessus que dans toute IFR, les temps et distances corrects mesurés entre tous les points seront les mêmes qu'au repos . Par conséquent, le nombre de périodes, par exemple, initiéesl'onde électromagnétique entre tous les points sera la même qu'au repos. Puisque la perturbation d'un champ d'une configuration arbitraire peut être représentée par une expansion dans une série d'harmoniques monochromatiques, les configurations et les intensités de tous les champs dans le système intrinsèque seront les mêmes au repos, respectivement. Par conséquent, les relations de phase et la synchronisation des champs qui forment le corps ne sont pas violées, et tous les processus en lui se dérouleront comme au repos.
C'est exactement ce que proclame le "principe de relativité" d'Einstein, et, comme on le voit, il est mathématiquement déduit inévitablement de deux hypothèses (voir chapitre 1), permettez-moi de vous rappeler: premièrement : que la position des particules réelles est déterminée par la structure des champs , et deuxièmement , quela propagation du champ se produit à une vitesse finie .
Autrement dit, le principe de relativité est déjà, pour ainsi dire, non a priori un principe universel , mais une conséquence, et a des limites claires d'applicabilité . En particulier, la vitesse de la lumière n'a pas la signification d'une constante mondiale, mais est une vitesse spécifique de la lumière dans une région spécifique de l'espace . Et à certains endroits, cela peut être différent en raison de l'interaction avec les champs physiques locaux, par exemple la gravité. Nous avons donc deux alternatives qui aboutissent exactement aux mêmes formules relativistes:
- d'abord, orthodoxe et scientifique: il faut postuler a priori un vrai principe de relativité ;
- : ,
Dans le premier cas, les phénomènes de SRT ne nécessitent pas d'explication, et leurs causes et mécanismes restent inconnaissables. La question "Pourquoi?" il s'avère même être en dehors de la science.
Dans le second , les hypothèses sont même assez logiques et il n'y a rien à postuler, et elles ne sont «fantastiques» que dans la mesure où d'autres raisons du relativisme sont acceptées en science. A la question "pourquoi les phénomènes SRT sont-ils comme ça?" ici une explication claire et même presque insignifiante est donnée. Mais il y a un besoin urgent de découvrir la nature de la matière et dans quelle relation elle est avec les champs physiques.
Par conséquent, nous continuerons à fantasmer davantage.
6. Dérivation de la formule E = Mc² et des équations de dynamique
Voyons d'abord comment les forces se transforment à des vitesses relativistes. Sélectionnons l'élément de volume du corps sur lequel agissent les moments de forces équilibrés. Lorsque le corps bouge, la taille longitudinale (le long de la trajectoire du mouvement) de l'élément sélectionné
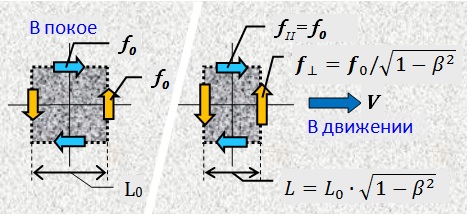diminue en fonction du coefficient de Lorentz. Pour que l'élément reste en équilibre, les forces perpendiculaires au mouvement doivent augmenter exactement dans le même rapport. Fig. 7.
L'ampleur des forces parallèles au mouvement ne changera pas. Le facteur de dépendance des forces sur l'orientation par rapport à la direction du mouvement doit être pris en compte dans l'expansion vectorielle des forces dans les formules suivantes.
Notez que l'accélération du corps à une certaine vitesse est effectuée par la force appliquée, qui, en conséquence, fait un certain travail, augmentant ainsi l'énergie du corps. ETQuelle est la différence entre un corps dispersé dans l'espace et un corps au repos? Le fait que l'overclocking soit compressé selon Lorentz . Au chapitre 1, une formule est dérivée pour le lieu des points (GMT) entourant un point donné, à partir duquel ils ont le même temps d'interaction des champs physiques. Ce GMT s'avère être un ellipsoïde compressé selon Lorentz dans le sens du mouvement. Faisons maintenant attention au fait que le volume W de cet ellipsoïde diminue proportionnellement à la contraction de Lorentz. Cela se reflète dans la formule (1) ci-dessous. Maintenant , nous allons faire une hypothèse vraiment fantastique quand un corps est accéléré, le travail de la force est consacré à la compression du volume de l' espace qu'il occupe, qui reste alors inchangée dans la libre circulation. Au moins, cette hypothèse n'est pas pire que la maxime scientifique selon laquelle l'espace peut se plier ou gonfler.
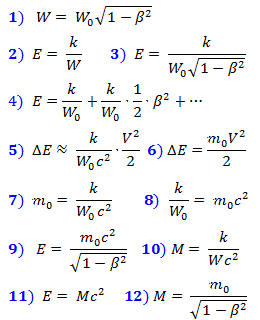Supposons que cette énergie E soit inversement proportionnelle au volume auquel il a été possible de la comprimer selon la formule (2), ou (3) après y avoir substitué (1).
Nous développons E de (3) dans une série de Taylor (4), d'où (5) est l'incrément d'énergie à partir de la vitesse dans la première approximation à de faibles vitesses. Mais à basse vitesse, il est également égal à (6). En comparant (5) et (6), nous obtenons (7) et (8). En remplaçant (8) par (3), nous obtenons (9), qui relie l'énergie d'un corps dans l'espace comprimé à sa masse de repos.
Exprimons la masse relativiste par la formule (10), d'où, en substituant (2), nous obtenons l'expression bien connue (11), reliant masse et énergie. En comparant (9) et (11), nous obtenons (12).
La masse n'est qu'une autre formulation de l'énergie dépensée dans l'espace de compression. Et en ce sens, ils sont équivalents. Et la substance "marque" seulement la zone d'espace occupée par le corps.
Changement de l'énergie totale E du système, c'est-à-dire l'énergie de compression de l'espace, en pleine conformité avec la mécanique classique newtonienne, est égale au travail de la force appliquée comme le produit de la force par trajet, et le changement de l'impulsion P du système est égal au produit de la même force et du temps de son action. Ces dépendances se reflètent dans les formules (13). Après y avoir substitué les expressions de l'énergie de (11) et de l'impulsion Pà partir de la formule (14),
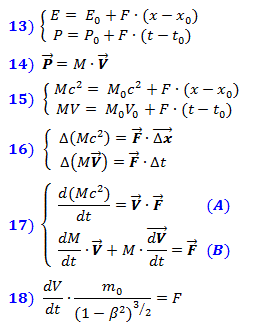nous obtenons le système d'équations (15), qui s'écrit sous forme de petits incréments dans (16) sous forme vectorielle. Puis, en différenciant par rapport au temps, nous notons le système d'équations différentielles (17) décrivant la dynamique relativiste. La force F n'a pas besoin d'être différenciée, car elle est externe et ne dépend pas des variations des variables système. En substituant l' expression de masse de (12) à la formule ( A ), nous obtenons la formule relativiste bien connue du mouvement rectiligne (18). 
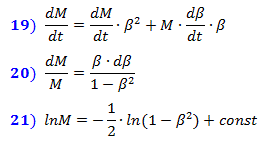A partir du système d'équations (17), il est possible de découvrir la dépendance de la masse sur la vitesse. Substituer F de la formule ( B ) dans la formule ( A ) et diviser les deux côtés de l'égalité par c², en accélérant le long de la trajectoire du mouvement, on obtient les expressions (19) et (20). D'où, intégrant, on obtient l'expression (21). Il est facile de voir qu'elle équivaut à l'expression logarithmique (12) pour la masse relativiste, où const est égal au logarithme de la masse restante m 0 . Cela signifie qu'une telle dépendance de la masse à la vitesse assure la correspondance de l'énergie Mc² et de l'impulsion M · V , dans les formules (16, 17). Et à partir de là, il s'ensuit également que la valeur que nous avons précédemment supposée comme la masse de repos est une constante indépendante de la vitesse, telle qu'elle est écrite dans les formules originales (9). Et cela signifie que notre hypothèse sur la dépendance de l'énergie sur le degré de compression spatiale est correcte.
Bien sûr, la revendication de la compression de l'espace n'est pas très convaincante. Si l'espace est censé être un contenant vide de particules et de corps, comment pouvez-vous compresser le vide? Le vide restera le vide. La science, cependant, se permet de parler de la courbure de l'espace vide - les formules l'exigent. Cependant, à proprement parler, son espace est une abstraction mathématique.
Mais nous pouvons tout à fait raisonnablement supposer que l' espace n'est pas vide, mais rempli d'une sorte de matière qui, supposons, non dans un état comprimé, est perçue par nous comme du vide.... Lorsque, par exemple, il est soumis à une contrainte de compression, nous avons des particules et des corps de matière. Lorsque ceux-ci sont au repos, le degré de compression (énergie) d'une section de cette matière correspond à la masse au repos du corps, et à son accélération, à la fois le degré de compression (énergie) du corps et l'augmentation de masse correspondante.
Et dans cet environnement matériel, les champs physiques qui déterminent la localisation et l'interaction des particules (jusqu'aux "très très" primaires - qui, nous continuons à fantasmer , s'avéreront être le phénomène de focalisation des champs de leur environnement sans lequel ils n'existent pas), peuvent bien exister et se propager à une vitesse spécifique ), dont l'énergie de repos et de mouvement est déterminée par le degré de compression de la zone de matière primaire qu'ils occupent . Réellement,les équations de la dynamique relativiste décrivent simplement le mouvement de ces inhomogénéités de contraintes (corps matériels) dans la matière première . Comme nous l'avons vu, il n'y a pas de contradictions avec l'expérience de Michelson et les transformations de Lorentz.