Clever Geek Handbook

Le paradoxe de l'anniversaire sur les données VK

salut!



J'ai décidé de vérifier le paradoxe de l'anniversaire en utilisant les données disponibles auprès de VK.



Quel est le paradoxe de l'anniversaire?



Essayez de répondre à la question: Combien de personnes dans une pièce sont nécessaires pour que deux personnes fêtent le même anniversaire avec une probabilité de 0,5? (date et mois). Le paradoxe de l'anniversaire répond à cette question.



Afin de résoudre le problème, il convient de souligner plusieurs conditions préalables:



  1. Le modèle n'aura pas le 29 février => 365 jours par an dans le modèle
  2. Chacun des 365 jours est également probable.


Bien sûr, il n'est pas tout à fait réaliste que les anniversaires soient également probables - il y a des effets saisonniers qui affectent les dates de naissance des enfants, je pense que vous pouvez vous-même deviner quoi ...



La plupart des gens répondent intuitivement à la question du problème: 180. Cela semble logique, il faut 180 personnes pour avoir probabilité de 0,5 anniversaire identique (365 jours au total). Tous ceux qui n'ont jamais entendu parler du paradoxe de l'anniversaire parlent de cette intuition. La bonne réponse est en fait bien inférieure à 180, voire 150, voire 100: 23.



Au moins 1 anniversaire correspondant est requis - je peux donc trouver la probabilité qu'il n'y ait pas d'anniversaires correspondants:

P(" ")=365∗364∗363∗...∗(365−k+1)365k=365!365k∗(365−k)!

.

L'idée est la suivante: je prends la première personne et me souviens de son anniversaire, puis la seconde et je calcule la probabilité que son anniversaire ne coïncide pas avec l'anniversaire de la première; plus loin que le troisième et je calcule la probabilité que son anniversaire ne coïncide pas avec les anniversaires du premier et du deuxième.



En résolvant l'équation, il s'avère que 23 personnes sont nécessaires et que la probabilité d'anniversaires coïncidents sera de 0,5073, avec 100 personnes, la probabilité est de 0,9999.



Voyons le paradoxe sur les données VK?



En théorie, avec 23 personnes, la probabilité d'anniversaires coïncidant est de 0,5073, avec 50 personnes 0,97 et avec 100 0,99. Vérifions-le via l'API VK.



1. Je choisis une grande communauté à VK. J'ai décidé de prendre le groupe MDK sur Vkontakte ...



Tout d'abord, je crée un fichier csv avec les colonnes dont j'ai besoin. 



with open('vk_data.csv', 'w') as new_file:
                # csv
                fieldnames = ['id', 'bdate', 'bmonth', 'byear', 'dandm']

                csv_writer = csv.DictWriter(new_file, fieldnames=fieldnames, delimiter=',')

                csv_writer.writeheader()

                newDict = dict()


Je me connecte à VK via l'API et définit le public dont j'ai besoin 

vk_session = vk_api.VkApi('username', 'password')
                vk_session.auth()

                vk = vk_session.get_api()
                
                vk_group = vk.groups.getMembers(group_id = 'mudakoff', fields = 'bdate')


Nous commençons à analyser VKontakte, leur API vous permet d'analyser seulement 1000 utilisateurs, donc je crée une boucle. 



for i in range(0, 20):
                    vk_group = vk.groups.getMembers(group_id = 'mudakoff', offset = 1000 * i,  fields = 'bdate')
                    for k in range(0, 1000):
                        try:
                            new_file.write(str(vk_group['items'][k]["id"]) + ',' + str(vk_group['items'][k]["bdate"]).replace('.', ','))
                            new_file.write('\n')
                        except:
                            pass


En théorie, nous avons supposé que les anniversaires sont également probables, mais que se passe-t-il en pratique? Je vais construire un histogramme des anniversaires.



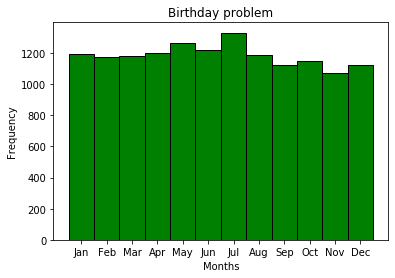
image



Les anniversaires par mois ne sont pas des événements équiprobables, ce qui est généralement assez logique - ce n'est qu'une condition préalable pour résoudre le problème de l'anniversaire. Évidemment, il y aura différents événements saisonniers, pour différents endroits. Pour une raison quelconque, juillet est le mois le plus populaire pour l'anniversaire des abonnés MDK.



J'estimerai empiriquement la probabilité que dans un groupe de 50 personnes arbitraires, il y en ait au moins deux avec le même anniversaire. Pour ce faire, j'ai écrit un cycle au cours duquel un sous-échantillon de 50 lignes provient du tableau. Pour ces 50 lignes à l'intérieur de la condition, j'ai vérifié le match des anniversaires. Si cela correspond, je m'en souviens dans la variable compteur, que je diviserai par la suite par la longueur du cycle pour obtenir la probabilité. 



fifty = df["dandm"].sample(n = 50)
for i in range(0, 1000):
    fifty = df["dandm"].sample(n = 50)
    for j in fifty.duplicated():
        if j == True:
            counter = counter + 1
            break
print(':', counter / 1000)


La probabilité est obtenue dans la région de 0,97, ce qui coïncide avec les données théoriques.



Production



Il était intéressant de voir comment la théorie se rapporte à l'empirisme, et dans ce cas, les données confirment la théorie. Il convient de noter que le résultat est représentatif, car l'échantillon est suffisamment grand - 20 000 personnes.



Ressources



  1. Université de Harvard. Problème d'anniversaire, propriétés de probabilité | Statistiques 110. URL: www.youtube.com/watch?v=LZ5Wergp_PA&t=150s . Consulté le 07/08/2020
  2. Problème d'anniversaire. URL: en.wikipedia.org/wiki/Birthday_problem . Consulté le 07/08/2020>


More articles:


All Articles