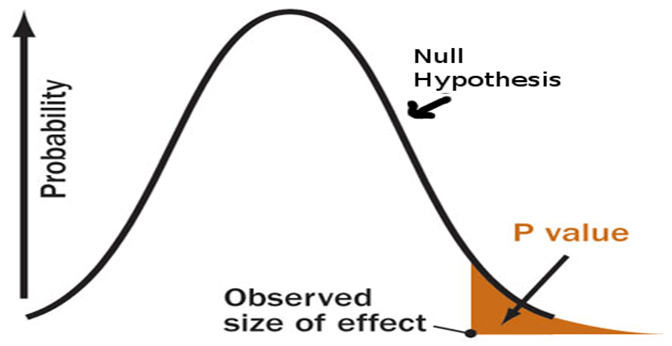
À l'époque, je ne savais rien de la valeur p, des tests d'hypothèse ou même de la signification statistique.
J'ai décidé de rechercher sur Google le mot «valeur p», et ce que j'ai trouvé sur Wikipédia m'a rendu encore plus confus ...
Lors du test d'hypothèses statistiques, la valeur p ou la valeur de probabilité pour un modèle statistique donné est la probabilité que, si l'hypothèse nulle est vraie, le résumé statistique (par exemple, la valeur absolue de la moyenne de l'échantillon de la différence entre deux groupes de comparaison) sera supérieur ou égal aux résultats réels observés.Bon travail, Wikipedia.
- Wikipédia
D'accord. Je n'ai pas compris ce que signifie réellement la valeur p.
En approfondissant le domaine de la science des données, j'ai finalement commencé à comprendre la signification de la valeur p et où elle peut être utilisée dans le cadre d'outils d'aide à la décision dans certaines expériences.
J'ai donc décidé d'expliquer la valeur p dans cet article, ainsi que la façon dont elle peut être utilisée dans les tests d'hypothèse, pour vous donner une compréhension meilleure et plus intuitive des valeurs p.
Nous ne pouvons pas non plus manquer une compréhension fondamentale d'autres concepts et la définition de la valeur p, je promets que je vais rendre cette explication intuitive sans vous exposer à tous les termes techniques que j'ai rencontrés.
Il y a quatre sections au total dans cet article pour vous donner une image complète de la construction d'un test d'hypothèse à la compréhension de la valeur p et à son utilisation dans votre processus de prise de décision. Je vous recommande vivement de les parcourir tous pour avoir une compréhension détaillée des valeurs p:
- Tests d'hypothèses
- Distribution normale
- Qu'est-ce qu'une valeur P?
- Signification statistique
Ça va être amusant.
Commençons!
1. Test des hypothèses
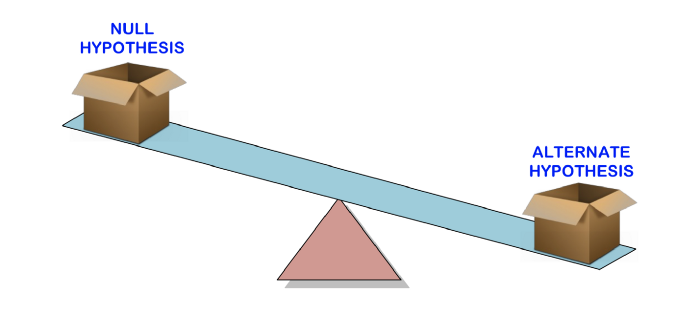
Avant de parler de ce que signifie la valeur p, commençons par examiner les tests d'hypothèse , où la valeur p est utilisée pour déterminer la signification statistique de nos résultats.
Notre objectif ultime est de déterminer la signification statistique de nos résultats.
Et la signification statistique repose sur ces 3 idées simples:
- Tests d'hypothèses
- Distribution normale
- Valeur p
Le test d'hypothèse est utilisé pour tester la validité d'une déclaration (hypothèse nulle) faite sur une population à l'aide d'échantillons de données. Une autre hypothèse est celle que vous croiriez si l'hypothèse nulle se révélait fausse.
En d'autres termes, nous allons créer une réclamation (hypothèse nulle) et utiliser les exemples de données pour vérifier si la réclamation est valide. Si l'énoncé n'est pas vrai, nous choisirons une hypothèse alternative. Tout est très simple.
Pour savoir si une affirmation est valide ou non, nous utiliserons la valeur p pour évaluer la force de la preuve pour voir si elle est statistiquement significative. Si la preuve soutient l'hypothèse alternative, alors nous rejetons l'hypothèse nulle et acceptons l'hypothèse alternative. Cela sera expliqué dans la section suivante.
Utilisons un exemple pour clarifier ce concept, et cet exemple sera utilisé tout au long de cet article pour d'autres concepts.
Exemple. Supposons qu'une pizzeria affirme que le délai de livraison est de 30 minutes ou moins en moyenne, mais que vous pensez qu'il est plus long que ce qu'elle prétend. Vous faites donc un test d'hypothèse et sélectionnez au hasard un délai de livraison pour tester la réclamation:
- — 30
- — 30
- , , — — , .
Nous utiliserons un test à sens unique dans notre cas, car il est seulement important pour nous que le délai moyen de livraison dépasse 30 minutes. Nous n'envisagerons pas cette possibilité dans l'autre sens, car les conséquences d'un délai moyen de livraison inférieur ou égal à 30 minutes sont encore plus préférables. Ici, nous voulons vérifier s'il y a une chance que le délai de livraison moyen soit supérieur à 30 minutes. En d'autres termes, nous voulons voir si la pizzeria nous a trompés.
L'un des moyens courants de tester des hypothèses consiste à utiliser le test Z. Nous n'entrerons pas dans les détails ici, car nous voulons mieux comprendre ce qui se passe en surface avant de plonger plus profondément.
2. Distribution normale
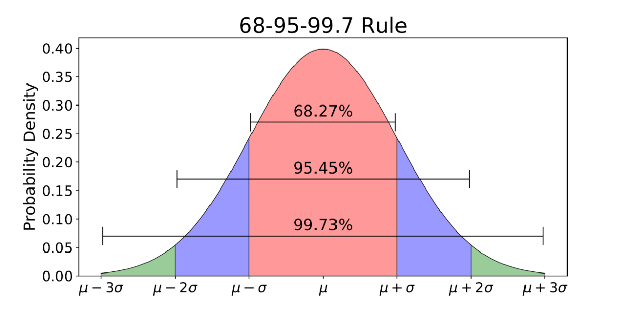
La distribution normale est une fonction de densité de probabilité utilisée pour visualiser la distribution des données.
La distribution normale a deux paramètres, la moyenne (μ) et l'écart type, également appelé sigma (σ).
La moyenne est la tendance centrale de la distribution. Il définit l'emplacement du pic pour les distributions normales. L'écart type est une mesure de la variabilité. Il détermine à quelle distance de la moyenne les valeurs ont tendance à chuter.
La distribution normale est généralement associée à la règle 68-95-99.7 (image ci-dessus).
- 68% des données sont à moins d'un écart-type (σ) de la moyenne (μ)
- 95% des données sont à moins de 2 écarts-types (σ) de la moyenne (μ)
- 99,7% des données sont à moins de 3 écarts-types (σ) de la moyenne (μ)
Vous vous souvenez du seuil de cinq sigma pour le boson de Higgs dont j'ai parlé au début? 5 sigma représente environ 99,99999426696856% des données qui doivent être reçues avant que les scientifiques ne confirment la découverte du boson de Higgs. Il s'agissait d'un seuil strict pour éviter d'éventuels faux signaux.
Cool. Maintenant, vous vous demandez peut-être: "Comment la distribution normale est-elle liée à nos tests d'hypothèse précédents?"
Puisque nous avons utilisé le test Z pour tester notre hypothèse, nous devons calculer les scores Z (qui seront utilisés dans nos statistiques de test), qui sont le nombre d'écarts types par rapport à la moyenne du point de données. Dans notre cas, chaque point de données correspond au délai de livraison de la pizza que nous avons reçu. Notez que lorsque nous avons calculé tous les scores Z pour chaque heure de livraison de pizza et tracé une courbe de distribution normale standard comme indiqué ci-dessous, l'unité sur l'axe X passera des minutes à l'unité d'écart type lorsque nous avons standardisé la variable en soustrayant la moyenne et en divisant son par l'écart type (voir la formule ci-dessus). L'examen de la courbe en cloche standard est utile car nous pouvons comparer les résultats des tests avec une population «normale» avec une unité standardisée en écart type, en particulier lorsque nous avons une variable qui vient avec différentes unités.

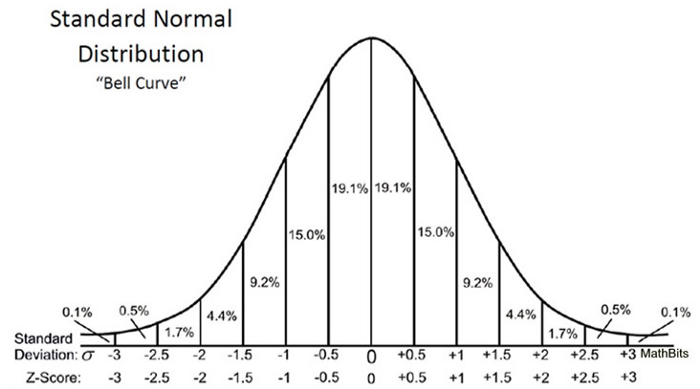
Un score z peut nous dire où se trouvent les données globales par rapport à la population moyenne.
J'aime la façon dont Will Cursen le dit: plus le score Z est élevé ou bas, moins il y a de chances qu'un résultat aléatoire soit et plus un résultat significatif sera probable.
Mais à quel point est-il considéré comme suffisamment élevé (ou faible) pour quantifier l'importance de nos résultats?
Climax
Ici, nous avons besoin de la dernière pièce pour résoudre le casse-tête, la valeur p et vérifier si nos résultats sont statistiquement significatifs en fonction du niveau de signification (également appelé alpha) que nous avons défini avant de commencer notre expérience.
3. Qu'est-ce que la valeur P?
Enfin ... Nous parlons ici de valeur p!
Toutes les explications précédentes ont pour but de préparer le terrain et de nous conduire à cette valeur P. Nous avons besoin du contexte et des étapes précédentes pour comprendre cette valeur p mystérieuse (en fait pas si mystérieuse) et comment elle pourrait conduire à nos décisions de tester l'hypothèse.
Si vous êtes arrivé jusqu'ici, continuez à lire. Parce que cette section est la partie la plus excitante de toutes!
Au lieu d'expliquer les valeurs p en utilisant la définition de Wikipedia (désolé Wikipedia), expliquons-le dans notre contexte - le délai de livraison de la pizza!
Pour rappel, nous avons sélectionné au hasard certains délais de livraison de pizzas, et le but est de vérifier si le délai de livraison dépasse 30 minutes. Si les preuves finales étayent la demande de la pizzeria (le délai de livraison moyen est de 30 minutes ou moins), nous ne rejetterons pas l'hypothèse nulle. Sinon, nous réfutons l'hypothèse nulle.
Le travail de la valeur p est donc de répondre à cette question:
Si je vis dans un monde où les délais de livraison de pizzas sont de 30 minutes ou moins (l'hypothèse nulle est correcte), à quel point mes preuves sont-elles inattendues dans la vraie vie?La valeur p répond à cette question avec un nombre - une probabilité.
Plus la valeur de p est basse, plus l'évidence est inattendue, plus notre hypothèse nulle paraît ridicule.
Et que faisons-nous lorsque nous nous sentons ridicules à propos de notre hypothèse nulle? Nous la rejetons et choisissons notre hypothèse alternative.
Si la valeur p est inférieure à un niveau de signification donné (les gens l'appellent alpha, j'appelle cela le seuil de l'absurdité - ne demandez pas pourquoi, c'est juste plus facile pour moi de comprendre), alors nous rejetons l'hypothèse nulle.
Nous comprenons maintenant ce que signifie la valeur p. Appliquons ceci dans notre cas.
Valeur p dans le calcul du délai de livraison de la pizza
Maintenant que nous avons collecté des exemples de données sur les délais de livraison, nous avons effectué le calcul et constaté que le délai de livraison moyen est de 10 minutes de plus avec une valeur p de 0,03.
Cela signifie que dans un monde où les délais de livraison des pizzas sont de 30 minutes ou moins (l'hypothèse nulle est correcte), il y a 3% de chances que nous voyions le délai de livraison moyen au moins 10 minutes de plus en raison du bruit aléatoire. ...
Plus la valeur p est petite, plus le résultat sera significatif, car il est moins susceptible d'être causé par le bruit.
Dans notre cas, la plupart des gens comprennent mal la valeur p:
Une valeur p de 0,03 signifie qu'il y a 3% (probabilité en pourcentage) que le résultat soit dû au hasard - ce qui n'est pas vrai.Les gens veulent souvent une réponse définitive (moi y compris), c'est pourquoi je suis confus depuis longtemps avec l'interprétation des p-values.
La valeur p ne * prouve * rien. C'est juste une façon d'utiliser la surprise comme base d'une décision intelligente.Voici comment nous pouvons utiliser une valeur p de 0,03 pour nous aider à prendre des décisions intelligentes (IMPORTANT):
- Cassie Kozyrkov
- Imaginez que nous vivons dans un monde où le délai de livraison moyen est toujours de 30 minutes ou moins - parce que nous croyons en la pizzeria (notre croyance d'origine)!
- Après avoir analysé le délai de livraison des échantillons collectés, la valeur p est inférieure de 0,03 au niveau de signification de 0,05 (en supposant que nous définissions cette valeur avant notre expérience) et nous pouvons dire que le résultat est statistiquement significatif.
- , 30 , , , , .
- ? ( ) . , , , , , , .
- , — .
A présent, vous avez peut-être déjà compris quelque chose ... Selon notre contexte, les valeurs p ne sont pas utilisées pour prouver ou justifier quoi que ce soit.
À mon avis, les valeurs p sont utilisées comme un outil pour contester notre croyance initiale (hypothèse nulle) lorsque le résultat est statistiquement significatif. Au moment où nous nous sentons ridicules avec notre propre croyance (en supposant que la valeur p indique que le résultat est statistiquement significatif), nous rejetons notre croyance originale (rejetons l'hypothèse nulle) et prenons une décision intelligente.
4. Importance statistique
Enfin, c'est la dernière étape où nous mettons tout ensemble et vérifions si le résultat est statistiquement significatif.
Il ne suffit pas d'avoir seulement une valeur p, nous devons fixer un seuil (niveau de signification - alpha). Alpha doit toujours être défini avant d'expérimenter pour éviter les biais. Si la valeur p observée est inférieure à alpha, nous concluons que le résultat est statistiquement significatif.
La règle de base est de définir alpha sur 0,05 ou 0,01 (encore une fois, la valeur dépend de votre tâche).
Comme mentionné précédemment, supposons que nous définissions l'alpha à 0,05 avant de commencer l'expérience, le résultat est statistiquement significatif puisque la valeur p de 0,03 est inférieure à l'alpha.
Pour votre information, voici les principales étapes de l'ensemble de l'expérience:
- Formuler l'hypothèse nulle
- Former une hypothèse alternative
- Déterminez la valeur alpha à utiliser
- Trouvez le Z-score associé à votre niveau alpha
- Trouvez des statistiques de test à l'aide de cette formule
- Si la statistique du test est inférieure au score Z alpha (ou si la valeur p est inférieure à la valeur alpha), rejetez l'hypothèse nulle. Sinon, ne rejetez pas l'hypothèse nulle.
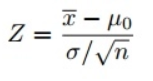
Si vous souhaitez en savoir plus sur la signification statistique, n'hésitez pas à consulter cet article - Expliquer la signification statistique , écrit par Will Kersen .
Réflexions ultérieures
Il y a beaucoup à digérer ici, n'est-ce pas?
Je ne peux pas nier que les valeurs p sont intrinsèquement déroutantes pour de nombreuses personnes, et il m'a fallu un certain temps pour vraiment comprendre et apprécier les valeurs p et comment elles pourraient être appliquées dans notre processus de prise de décision. en tant que data scientists.
Mais ne vous fiez pas trop aux valeurs p, car elles ne vous aident que dans une petite partie de l'ensemble du processus de prise de décision.
J'espère que mon explication des valeurs p est devenue intuitive et utile dans votre compréhension de ce que signifient réellement les valeurs p et comment elles peuvent être utilisées pour tester vos hypothèses.
Le calcul des valeurs p est simple en soi. Le plus dur vient lorsque nous voulons interpréter les valeurs p dans les tests d'hypothèse. Espérons que maintenant la partie difficile deviendra un peu plus facile pour vous.
Si vous souhaitez en savoir plus sur les statistiques, je vous recommande vivement de lire ce livre (que je suis en train de lire!) - Statistiques pratiques pour les scientifiques des données, spécialement écrit pour les scientifiques des données afin de comprendre les concepts fondamentaux des statistiques.

Apprenez-en plus sur la façon d'obtenir une profession de haut niveau à partir de zéro ou de monter en gamme en termes de compétences et de salaire en suivant les cours en ligne rémunérés de SkillFactory:
- Formation au métier de Data Science à partir de zéro (12 mois)
- Profession d'analyste avec tout niveau de départ (9 mois)
- Machine Learning (12 )
- «Python -» (9 )
- DevOps (12 )
- - (8 )