Nous comprenons et créons
La bonne nouvelle avant l'article: de bonnes compétences en mathématiques pour lire et (espérons-le!) Compréhension ne sont pas nécessaires.
Clause de non-responsabilité: la partie code de cet article, comme la précédente , est une traduction adaptée, complétée et testée. Je suis reconnaissant à l'auteur, car c'est l'une de mes premières expériences dans le code, après quoi j'ai inondé encore plus. J'espère que mon adaptation fonctionnera de la même manière pour vous!
Alors allons-y!
La structure est comme ceci:
- Qu'est-ce qu'une chaîne de Markov?
- Un exemple du fonctionnement de la chaîne
- Matrice de transition
- Modèle de chaîne de Markov avec Python - génération de texte basée sur les données
Qu'est-ce qu'une chaîne de Markov?
La chaîne de Markov est un outil de la théorie des processus aléatoires, constitué d'une séquence de n nombre d'états. Dans ce cas, les connexions entre les nœuds (valeurs) de la chaîne ne sont créées que si les états sont strictement les uns à côté des autres.
En gardant à l'esprit le mot de type gras uniquement , déduisons la propriété de la chaîne de Markov: La
probabilité d'un certain nouvel état dans la chaîne ne dépend que de l'état présent et ne prend pas mathématiquement en compte l'expérience des états passés => Une chaîne de Markov est une chaîne sans mémoire.
En d'autres termes, un nouveau sens danse toujours à partir de celui qui le tient directement par la poignée.
Un exemple du fonctionnement de la chaîne
Comme l'auteur de l'article dont est empruntée l'implémentation du code, prenons une séquence aléatoire de mots.
Début - artificiel - manteau de fourrure - artificiel - nourriture - artificiel - pâtes - artificiel - manteau de fourrure - artificiel - fin
Imaginons qu'il s'agit en fait d'un grand verset et que notre tâche est de copier le style de l'auteur. (Mais cela est, bien sûr, contraire à l'éthique)
Comment décider?
La première chose évidente que je veux faire est de compter la fréquence des mots (si nous devions faire cela avec un texte en direct, il serait d'abord utile de normaliser - d'amener chaque mot à un lemme (forme de dictionnaire)).
Début == 1
Artificiel == 5
Manteau de fourrure == 2
Pâtes == 1
Nourriture == 1
Fin == 1
En gardant à l'esprit que nous avons une chaîne de Markov, nous pouvons tracer graphiquement la distribution des nouveaux mots en fonction des précédents:

Verbalement:
- l'état de la fourrure, de la nourriture et des pâtes à 100% entraîne l'état artificiel p = 1
- l'état «artificiel» peut conduire à 4 conditions avec une probabilité égale, et la probabilité d'arriver à l'état d'un manteau de fourrure artificielle est plus élevée que les trois autres
- l'état final ne mène nulle part
- l'état «départ» à 100% entraîne l'état «artificiel»
Cela a l'air cool et logique, mais la beauté visuelle ne s'arrête pas là! Nous pouvons également construire une matrice de transition, et sur sa base, nous pouvons faire appel à la justice mathématique suivante:

Ce qui signifie en russe «la somme d'une série de probabilités pour un événement k, en fonction de i == la somme de toutes les valeurs des probabilités de l'événement k, en fonction de l'occurrence de l'état i, où l'événement k == m + 1, et l'événement i == m (c'est-à-dire que l'événement k diffère toujours de un de i) ».
Mais d'abord, comprenons ce qu'est une matrice.
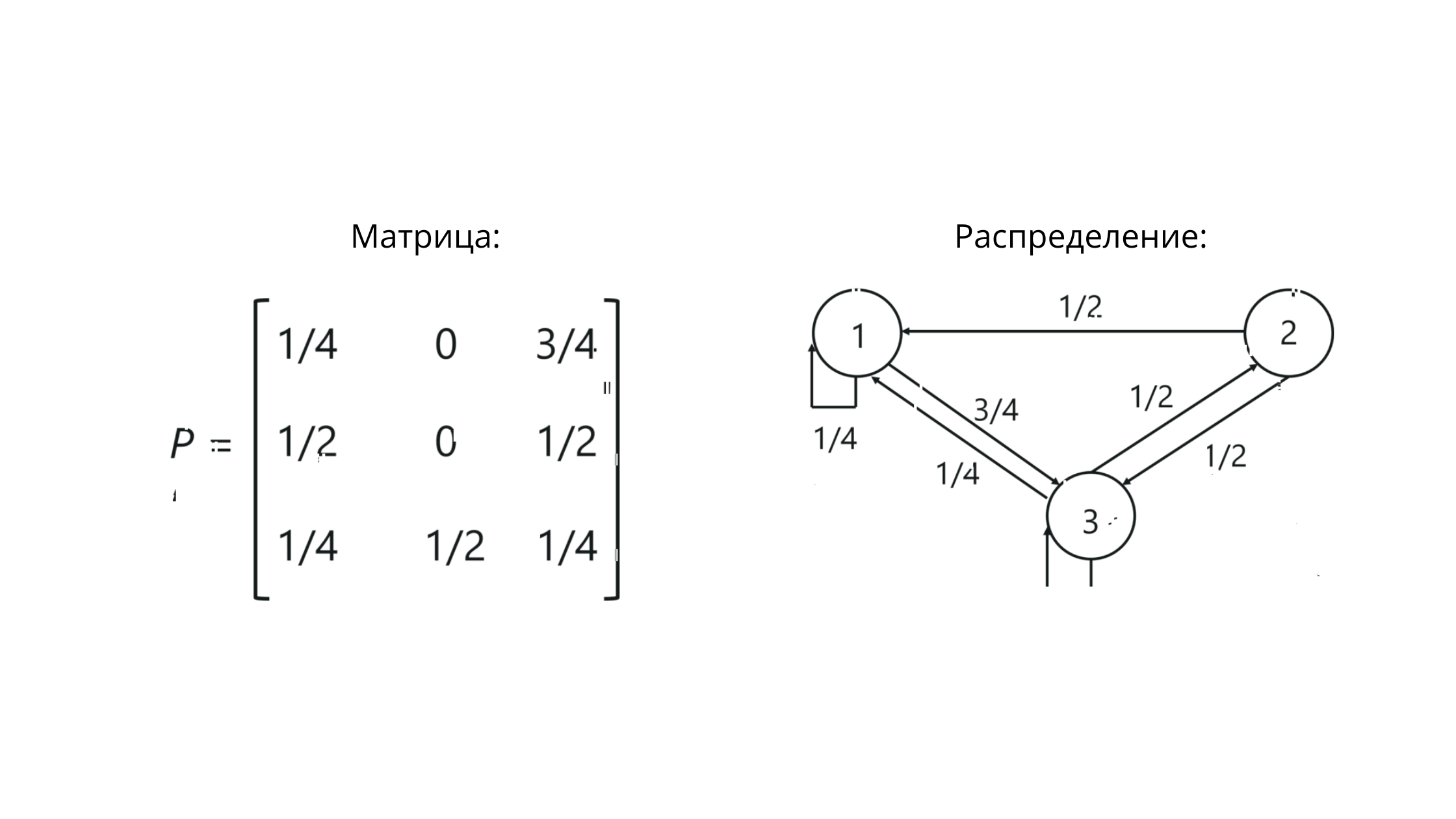
Matrice de transition
Lorsque nous travaillons avec des chaînes de Markov, nous avons affaire à une matrice de transition stochastique - un ensemble de vecteurs, dans lequel les valeurs reflètent les valeurs des probabilités entre les gradations.
Oui, oui, ça sonne.
Mais cela n'a pas l'air si effrayant:

P est la notation d'une matrice. Les valeurs à l'intersection des colonnes et des lignes reflètent ici les probabilités de transitions entre les états.
Pour notre exemple, cela ressemblera à ceci:

Notez que la somme des valeurs de la ligne == 1. Cela signifie que nous avons tout construit correctement, car la somme des valeurs de la ligne de la matrice stochastique doit être égale à un.
Exemple nu sans manteaux et pâtes en fausse fourrure: Un
exemple même nu est la matrice d'identité pour:
- le cas où il est impossible de passer de A à B, et de B - à A [1]
- le cas où le passage de A à B est possible [2]

Respecto. Avec la théorie terminée.
Nous utilisons Python.
Un modèle basé sur la chaîne de Markov utilisant Python - génération de texte basé sur des données
Étape 1
Importez le package approprié pour le travail et récupérez les données.
import numpy as np
data = open('/Users/sad__sabrina/Desktop/1.txt', encoding='utf8').read()
print(data)
, , , , ( « memorylessness »). , , , , , , ; .., , .
Ne vous concentrez pas sur la structure du texte, mais faites attention à l'encodage utf8. Ceci est important pour lire les données.
Étape 2
Divisez les données en mots.
ind_words = data.split()
print(ind_words)
['\ufeff', '', '', '', '', ',', '', '', ',', '', '', '', '', '', '', '', ',', '', '', '', ',', '', '', '', '', '(', '', '', '«', 'memorylessness', '»).', '', ',', '', '', '', '', ',', '', '', '', '', '', '', '', ',', '', '', '', '', '', '', '', '', '', ',', '', '', '', '', '', '', '', ',', '', '', ',', '', '', '', ';', '..,', '', '', '', '', ',', '', '', '', '', '', '', '.']Étape 3
Créons une fonction pour lier des paires de mots.
def make_pairs(ind_words):
for i in range(len(ind_words) - 1):
yield (ind_words[i], ind_words[i + 1])
pair = make_pairs(ind_words)La principale nuance de la fonction dans l'utilisation de l'opérateur yield (). Cela nous aide à répondre au critère de chaînage de Markov - le critère de stockage sans mémoire. Avec yield, notre fonction créera de nouvelles paires lors de ses itérations (répétitions), plutôt que de tout stocker.
Un malentendu peut surgir ici, car un mot peut se transformer en mots différents. Nous allons résoudre ce problème en créant un dictionnaire pour notre fonction.
Étape 4
word_dict = {}
for word_1, word_2 in pair:
if word_1 in word_dict.keys():
word_dict[word_1].append(word_2)
else:
word_dict[word_1] = [word_2]Ici:
- si nous avons déjà une entrée sur le premier mot d'une paire dans le dictionnaire, la fonction ajoute la valeur potentielle suivante à la liste.
- sinon: une nouvelle entrée est créée.
Étape 5
Choisissons au hasard le premier mot et, pour rendre le mot vraiment aléatoire, définissons la condition while en utilisant la méthode de chaîne islower (), qui satisfait True si la chaîne contient des lettres minuscules, permettant la présence de nombres ou de symboles.
Dans ce cas, nous fixerons le nombre de mots à 20.
first_word = np.random.choice(ind_words)
while first_word.islower():
chain = [first_word]
n_words = 20
first_word = np.random.choice(ind_words)
for i in range(n_words):
chain.append(np.random.choice(word_dict[chain[-1]]))Étape 6
Commençons notre chose aléatoire!
print(' '.join(chain))
; .., , , (La fonction join () est une fonction permettant de travailler avec des chaînes. Entre parenthèses, nous avons spécifié un séparateur pour les valeurs dans la ligne (espace).
Et le texte ... eh bien, ça sonne comme une machine et presque logique.
PS Comme vous l'avez peut-être remarqué, les chaînes de Markov sont utiles en linguistique, mais leur application va au-delà du traitement du langage naturel. Ici et ici, vous pouvez vous familiariser avec l'utilisation des chaînes dans d'autres tâches.
PPS Si ma pratique du code s'est avérée incompréhensible pour vous, je joins l' article original . Assurez-vous d'appliquer le code dans la pratique - la sensation quand il "a été exécuté et généré" se recharge!
J'attends vos avis et je serai heureux d'avoir des commentaires constructifs sur l'article!