
Les problèmes de sécurité de l'information nécessitent l'étude et la solution d'un certain nombre de problèmes théoriques et pratiques dans l'interaction de l'information des abonnés du système. Notre doctrine de la sécurité de l'information formule la triple tâche d'assurer l'intégrité, la confidentialité et la disponibilité de l'information. Les articles présentés ici sont consacrés à l'examen des problèmes spécifiques de sa solution dans le cadre de divers systèmes et sous-systèmes étatiques. Auparavant, l'auteur a examiné dans 5 articles les questions de la garantie de la confidentialité des messages au moyen des normes étatiques. Le concept général du système de codage a également été donné par moi plus tôt .
introduction
Par ma formation de base, je ne suis pas mathématicien, mais en lien avec les disciplines que je lis à l'université, j'ai dû le comprendre méticuleusement. Pendant longtemps et avec persistance, j'ai lu les manuels classiques de nos principales universités, une encyclopédie mathématique en cinq volumes, de nombreuses brochures populaires minces sur certaines questions, mais la satisfaction ne s'est pas manifestée. La compréhension profonde de la lecture ne s'est pas non plus produite.
Tous les classiques mathématiques se concentrent, en règle générale, sur le cas théorique infini, et les disciplines spéciales sont basées sur le cas des constructions finies et des structures mathématiques. La différence d'approche est colossale, l'absence ou le manque de bons exemples complets est peut-être le principal inconvénient et le manque de manuels universitaires. Il y a très rarement un livre de problèmes avec des solutions pour les débutants (pour les étudiants de première année), et ceux qui existent sont coupables d'omissions dans les explications. En général, je suis tombé amoureux des librairies techniques d'occasion, grâce auxquelles la bibliothèque et, dans une certaine mesure, le stock de connaissances ont été reconstitués. J'ai eu la chance de lire beaucoup, beaucoup, mais "je n'y suis pas allé".
Ce chemin m'a conduit à la question, que puis-je faire tout seul sans livre "béquilles", n'ayant devant moi qu'une feuille de papier vierge et un crayon avec une gomme? Cela s'est avéré être un peu et pas tout à fait ce qu'il fallait. Le chemin difficile de l'auto-éducation au hasard a été franchi. La question était la suivante. Puis-je construire et m'expliquer, tout d'abord à moi-même, le travail de code qui détecte et corrige les erreurs, par exemple, le code Hamming, (7, 4) -code?
On sait que le code de Hamming est largement utilisé dans de nombreuses applications dans le domaine du stockage et de l'échange de données, notamment en RAID; de plus, il est en mémoire ECC et permet la correction à la volée des erreurs simples et doubles.
Sécurité de l'information. Codes, chiffrements, messages steg
L'interaction d'informations par l'échange de messages entre ses participants devrait être protégée à différents niveaux et par divers moyens, tant matériels que logiciels. Ces outils sont développés, conçus et créés dans le cadre de certaines théories (voir figure A) et technologies adoptées par des accords internationaux sur les modèles OSI / ISO.
La protection de l'information dans les systèmes d'information et de télécommunication (STI) devient pratiquement le principal problème pour résoudre les problèmes de gestion, à la fois à l'échelle d'une personne individuelle - un utilisateur, et pour les entreprises, les associations, les services et l'État dans son ensemble. De tous les aspects de la protection ITKS, dans cet article, nous examinerons la protection des informations lors de leur extraction, traitement, stockage et transmission dans les systèmes de communication.
Pour clarifier davantage le sujet, nous nous concentrerons sur deux directions possibles, dans lesquelles deux approches différentes de la protection, de la présentation et de l'utilisation de l'information sont considérées: syntaxique et sémantique. Les abréviations suivantes sont utilisées dans la figure: codec - codec - décodeur; shidesh - un décodeur-décodeur; screech - correcteur - extracteur.
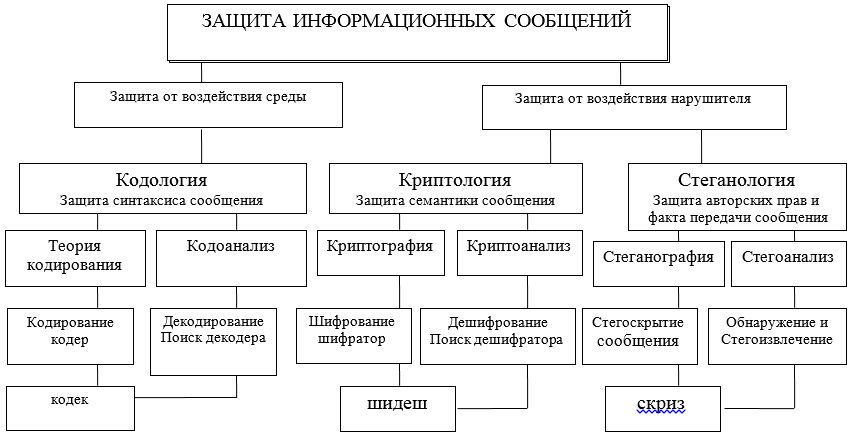
Figure A - Schéma des principales directions et interrelations des théories visant à résoudre les problèmes de protection de l'interaction des informations
Les caractéristiques syntaxiques de la présentation des messages vous permettent de contrôler et d'assurer l'exactitude et l'exactitude (sans erreur, intégrité) de la présentation pendant le stockage, le traitement, et en particulier lors du transfert d'informations via les canaux de communication. Ici, les principaux problèmes de protection sont résolus par les méthodes de codologie, sa grande partie - la théorie de la correction des codes.
Sécurité sémantique (sémantique)les messages sont fournis par les méthodes de cryptologie, qui au moyen de la cryptographie vous permet de vous protéger de la maîtrise du contenu des informations par un intrus potentiel. Dans ce cas, le contrevenant peut copier, voler, modifier ou remplacer, voire détruire le message et son support, mais il ne pourra pas obtenir d'informations sur le contenu et la signification du message transmis. Le contenu des informations contenues dans le message restera inaccessible au contrevenant. Ainsi, l'objet d'un examen plus approfondi sera la protection syntaxique et sémantique des informations dans l'ITCS. Dans cet article, nous nous limiterons à ne considérer que l'approche syntaxique dans une implémentation simple mais très importante du code correcteur.
Je vais immédiatement tracer une ligne de démarcation dans la résolution des problèmes de sécurité de l'information: la
théorie de la codologieconçu pour protéger les informations (messages) des erreurs (protection et analyse de la syntaxe des messages) du canal et de l'environnement, pour détecter et corriger les erreurs;
la théorie de la cryptologie est conçue pour protéger l'information d'un accès non autorisé à sa sémantique par l'intrus (protection de la sémantique, du sens des messages);
la théorie de la stéganologie est conçue pour protéger le fait de l'échange d'informations des messages, ainsi que pour protéger le droit d'auteur, les données personnelles (protection du secret médical).
En général, allons-y. Par définition, et il y en a pas mal, il n'est même pas facile de comprendre qu'il y a du code. Les auteurs écrivent que le code est un algorithme, un mappage et autre chose. Je n'écrirai pas sur la classification des codes ici, je dirai seulement que le code (7, 4) est un bloc .
À un moment donné, il m'est apparu que le code était constitué de mots de code spéciaux, un ensemble fini d'entre eux, qui sont remplacés par des algorithmes spéciaux avec le texte original du message du côté de transmission du canal de communication et qui sont envoyés par le canal au destinataire. Le remplacement est effectué par le dispositif codeur, et du côté réception, ces mots sont reconnus par le dispositif décodeur.
Le rôle des parties étant modifiable, ces deux appareils sont combinés en un seul et appelés codec abrégé (encodeur / décodeur) et sont installés aux deux extrémités du canal. De plus, comme il y a des mots, il y a aussi un alphabet. L'alphabet est composé de deux caractères {0, 1}, bloc binairecodes. L'alphabet en langage naturel (NL) est un ensemble de symboles - des lettres qui remplacent les sons de la parole orale lors de l'écriture. Ici, nous n'entrerons pas dans l'écriture hiéroglyphique en écriture syllabique ou nodulaire.
L'alphabet et les mots sont déjà une langue, on sait que les langues humaines naturelles sont redondantes, mais ce que cela signifie, là où réside la redondance linguistique est difficile à dire, la redondance n'est pas très bien organisée, chaotique. Lors du codage, du stockage des informations, ils ont tendance à réduire la redondance, par exemple, les archiveurs, le code Morse, etc.
Richard Hemming s'est probablement rendu compte plus tôt que d'autres que si la redondance n'est pas éliminée, mais raisonnablement organisée, elle peut être utilisée dans les systèmes de communication pour détecter les erreurs et les corriger automatiquement dans les mots de code du texte transmis. Il s'est rendu compte que les 128 mots binaires de 7 bits peuvent être utilisés pour détecter les erreurs dans les mots de code qui forment un code - un sous-ensemble de 16 mots binaires de 7 bits. C'était une supposition brillante.
Avant l'invention de Hamming, des erreurs étaient également détectées par le côté récepteur lorsque le texte décodé ne pouvait pas être lu ou qu'il ne s'avérait pas tout à fait ce qui était nécessaire. Dans ce cas, une demande a été envoyée à l'expéditeur du message pour répéter les blocs de certains mots, ce qui, bien entendu, était très gênant et ralentissait les sessions de communication. C'était un gros problème qui n'avait pas été résolu depuis des décennies.
Construction d'un (7, 4) code de Hamming
Revenons à Hamming. Les mots du code (7, 4) sont formés de 7 bits j = , j = 0 (1) 15, 4-informations et 3-symboles de contrôle, i.e. essentiellement redondants, car ils ne portent aucune information de message. Il était possible de représenter ces trois chiffres de contrôle par des fonctions linéaires de 4 symboles d'information dans chaque mot, ce qui assurait la détection du fait d'une erreur et sa place dans les mots afin de faire une correction. Un code (7, 4) a un nouvel adjectif et est devenu unbinaire de bloc linéaire.
Dépendances fonctionnelles linéaires (règles (*)) pour le calcul des valeurs de symbole
sont les suivants:
La correction de l'erreur est devenue une opération très simple - un caractère (zéro ou un) a été déterminé dans le bit erroné et remplacé par un autre opposé 0 par 1 ou 1 par 0. Combien de mots différents forment le code? La réponse à cette question pour le code (7, 4) est très simple. Puisqu'il n'y a que 4 chiffres d'information, et leur variété, lorsqu'ils sont remplis de symboles, a
= 16 options, alors il n'y a tout simplement pas d'autres possibilités, c'est-à-dire qu'un code composé de seulement 16 mots garantit que ces 16 mots représentent l'écriture entière de la langue entière.
Les parties informatives de ces 16 mots sont numérotées #
( ):
0 = 0000; 4 = 0100; 8 = 1000; 12 = 1100;
1 = 0001; 5 = 0101; 9 = 1001; 13 = 1101;
2 = 0010; 6 = 0110; 10 = 1010; 14 = 1110;
3 = 0011; 7 = 0111; 11 = 1011; 15 = 1111.
Chacun de ces mots de 4 bits doit être calculé et ajouté à droite par 3 bits de contrôle, qui sont calculés selon les règles (*). Par exemple, pour le mot d'information n ° 6 égal à 0110, nous avons et les calculs des symboles de contrôle donnent le résultat suivant pour ce mot:
Le sixième mot de code dans ce cas prend la forme:De la même manière, il est nécessaire de calculer les symboles de contrôle pour les 16 mots de code. Préparons un tableau K de 16 lignes pour les mots de code et remplissons séquentiellement ses cellules (je recommande au lecteur de le faire avec un crayon à la main).
Tableau K - mots de code j, j = 0 (1) 15, (7, 4) - Codes de Hamming
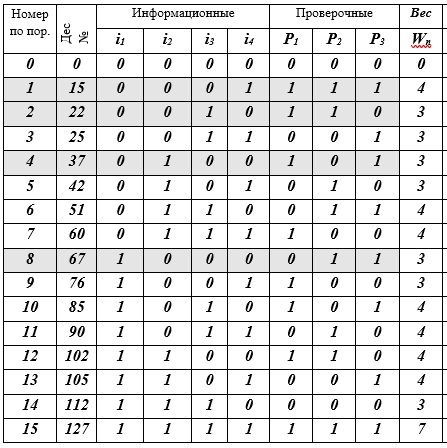
Description du tableau: 16 lignes - mots de code; 10 colonnes: numéro de séquence, représentation décimale du mot de code, 4 symboles d'information, 3 symboles de contrôle, le poids W du mot de code est égal au nombre de bits non nuls (≠ 0). 4 lignes de mots de code sont mises en évidence par remplissage - c'est la base du sous-espace vectoriel. En fait, c'est tout - le code est construit.
Ainsi, le tableau contient tous les mots (7, 4) - le code de Hamming. Comme vous pouvez le voir, ce n'était pas très difficile. Ensuite, nous parlerons des idées qui ont conduit Hamming à cette construction de code. Nous connaissons tous le code Morse, l'alphabet sémaphore naval et d'autres systèmes construits sur différents principes heuristiques, mais ici, en code (7, 4), des principes et des méthodes mathématiques rigoureux sont utilisés pour la première fois. L'histoire sera juste à leur sujet.
Fondements mathématiques du code. Algèbre supérieure
Le moment est venu de dire comment R. Hemming a eu l'idée d'ouvrir un tel code. Il n'avait aucune illusion particulière sur son talent et formulé modestement une tâche pour lui-même: créer un code qui détecterait et corrigerait une erreur dans chaque mot (en fait, même deux erreurs ont été détectées, mais une seule d'entre elles a été corrigée). Avec des chaînes de qualité, même une erreur est un événement rare. Par conséquent, le plan de Hemming était encore grandiose à l'échelle du système de communication. Il y a eu une révolution dans la théorie du codage après sa publication.
C'était en 1950. Je donne ici ma description simple (je l'espère, compréhensible), que je n'ai pas vue d'autres auteurs, mais il s'est avéré que tout n'est pas si simple. Il a fallu des connaissances dans de nombreux domaines des mathématiques et du temps pour tout comprendre profondément et comprendre par vous-même pourquoi cela a été fait de cette façon. Ce n'est qu'après cela que j'ai pu apprécier la belle et assez simple idée qui est implémentée dans ce code de correction. J'ai passé la plupart du temps à traiter de la technique des calculs et de la justification théorique de toutes les actions que j'écris ici.
Les créateurs des codes, pendant longtemps, n'ont pas pu penser à un code qui détecte et corrige deux erreurs. Les idées utilisées par Hemming n'y ont pas fonctionné. J'ai dû chercher et de nouvelles idées ont été trouvées. Très intéressant! Captive. Il a fallu environ 10 ans pour trouver de nouvelles idées, et seulement après cela, il y a eu une percée. Les codes indiquant un nombre arbitraire d'erreurs ont été reçus relativement rapidement.
Espaces vectoriels, champs et groupes . Le code (7, 4) résultant (tableau K) représente un ensemble de mots de code qui sont des éléments d'un sous-espace vectoriel (d'ordre 16, de dimension 4), c'est-à-dire partie d'un espace vectoriel de dimension 7 avec ordreSur les 128 mots, seulement 16 sont inclus dans le code, mais ils ont été inclus dans le code pour une raison.
Premièrement, ils sont un sous-espace avec toutes les propriétés et singularités qui en résultent; deuxièmement, les mots de code sont un sous-groupe d'un grand groupe d'ordre 128, et même un sous-groupe additif d'un champ de Galois étendu fini GF) degré d'expansion n = 7 et caractéristiques 2. Ce grand sous-groupe est décomposé en classes adjacentes par un sous-groupe plus petit, ce qui est bien illustré par le tableau D suivant. Le tableau est divisé en deux parties: supérieure et inférieure, mais il doit être lu comme une longue. Chaque classe adjacente (ligne du tableau) est un élément du groupe de facteurs par l'équivalence des composants.
Tableau D - Décomposition du groupe additif du champ de Galois GF () en cosets (lignes du tableau D) pour le sous-groupe du 16e ordre.
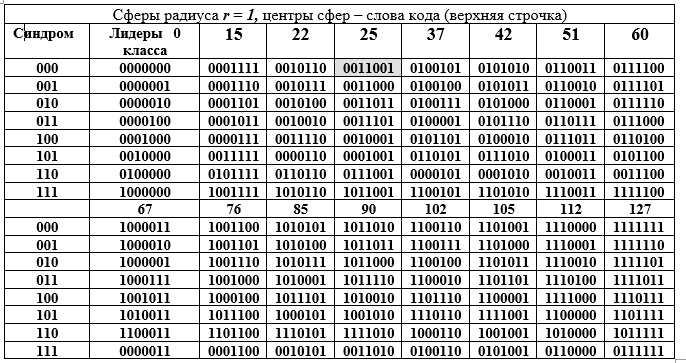
Les colonnes du tableau sont des sphères de rayon 1. La colonne de gauche (répétée) est le syndrome du mot (7, 4) code de Hamming, la colonne suivante représente les chefs de la classe contiguë. Ouvrons la représentation binaire de l'un des éléments (le 25e est mis en évidence par remplissage) du groupe de facteurs et sa représentation décimale:
Technique d'obtention des lignes du tableau D. Un élément de la colonne des chefs de file de la classe est additionné avec chaque élément de l'en-tête de la colonne du tableau D (la sommation est effectuée pour la rangée du chef sous forme binaire mod2). Puisque tous les chefs de classe ont un poids W = 1, alors toutes les sommes diffèrent du mot dans l'en-tête de colonne dans une seule position (la même pour la ligne entière, mais différente pour la colonne). Le tableau D a une merveilleuse interprétation géométrique. Les 16 mots de code sont représentés par les centres des sphères dans l'espace vectoriel à 7 dimensions. Tous les mots de la colonne diffèrent du mot supérieur dans la même position, c'est-à-dire qu'ils se trouvent sur la surface d'une sphère de rayon r = 1.
Cette interprétation cache l'idée de détecter une erreur dans n'importe quel mot de code. Nous travaillons avec des sphères. La première condition pour la détection d'erreur est que les sphères de rayon 1 ne doivent pas se toucher ou se croiser. Cela signifie que les centres des sphères sont à une distance de 3 ou plus les uns des autres. Dans ce cas, les sphères non seulement ne se croisent pas, mais ne se touchent pas non plus. Ceci est une exigence pour la non-ambiguïté de la décision: quelle sphère doit être attribuée au mot erroné reçu du côté récepteur par le décodeur (pas le code un de 128 -16 = 112).
Deuxièmement, l'ensemble des mots binaires de 7 bits de 128 mots est uniformément réparti sur 16 sphères. Le décodeur ne peut obtenir qu'un mot de cet ensemble de 128 mots connus avec ou sans erreur. Troisièmement, le côté récepteur peut recevoir un mot sans erreur ou avec distorsion, mais appartenant toujours à l'une des 16 sphères, ce qui est facilement déterminé par le décodeur. Dans cette dernière situation, il est décidé qu'un mot de code a été envoyé - le centre d'une sphère déterminé par le décodeur, qui a trouvé la position (intersection d'une ligne et d'une colonne) du mot dans le tableau D, c'est-à-dire les numéros de colonne et de ligne.
Ici, une exigence se pose pour les mots du code et pour le code dans son ensemble: la distance entre deux mots de code doit être d'au moins trois, c'est-à-dire la différence pour une paire de mots de code, par exemple, i = 85 == 1010101; j = 25 == 0011001 doit être au moins 3; 85 - 25 = 1010101 - 0011001 = 1001100 = 76, le poids du mot de différence W (76) = 3. (Le tableau D remplace le calcul des différences et des sommes). Ici, la distance entre les vecteurs de mots binaires est comprise comme le nombre de positions non concordantes dans deux mots. C'est la distance de Hamming, qui est devenue largement utilisée en théorie et en pratique, car elle satisfait tous les axiomes de la distance.
Remarque . Le code (7, 4) n'est pas seulement un code binaire en bloc linéaire , mais c'est aussi un code de groupe , c'est-à-dire que les mots du code forment un groupe algébrique par addition. Cela signifie que deux mots de code quelconques, lorsqu'ils sont ajoutés ensemble, donnent à nouveau l'un des mots de code. Seulement ce n'est pas une opération d'addition ordinaire, c'est l'addition modulo deux.
Tableau E - La somme des éléments du groupe (mots de code) utilisé pour construire le code de Hamming
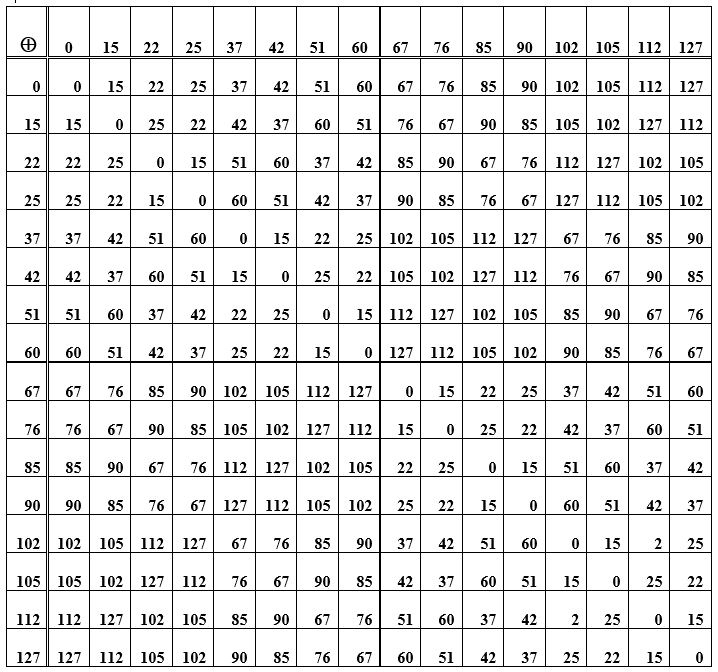
L'opération de sommation des mots elle-même est associative, et pour chaque élément de l'ensemble des mots de code, il y a un opposé, c'est-à-dire que la sommation du mot d'origine avec le contraire donne une valeur nulle. Ce mot de code zéro est l'élément neutre du groupe. Dans le tableau D, il s'agit de la diagonale principale des zéros. Les autres cellules (intersections ligne / colonne) sont des représentations numériques-décimales de mots de code obtenus en additionnant les éléments d'une ligne et d'une colonne. Lorsque vous réorganisez les mots par endroits (lors de la somme), le résultat reste le même; de plus, la soustraction et l'addition de mots donnent le même résultat. En outre, un système de codage / décodage qui met en œuvre le principe syndromique est considéré.
Application de code. Codeur
L'encodeur est situé du côté émission du canal et est utilisé par l'expéditeur du message. L'expéditeur du message (l'auteur) forme le message dans l'alphabet en langage naturel et le présente sous forme numérique. (Le nom du caractère en code ASCII et en binaire).
Il est pratique de générer des textes dans des fichiers pour un PC à l'aide d'un clavier standard (codes ASCII). Chaque caractère (lettre de l'alphabet) dans ce codage correspond à un octet de bits (huit bits). Pour le (7, 4) - code de Hamming, dans les mots desquels il n'y a que 4 symboles d'information, lors du codage d'un symbole de clavier en une lettre, deux mots de code sont nécessaires, c'est-à-dire un octet d'une lettre est divisé en deux mots d'information du langage naturel (NL) de la forme
...
Exemple 1 . Il est nécessaire de transférer le mot «chiffre» en NL. Nous entrons dans la table des codes ASCII, les lettres correspondent à: c –11110110, et –11101000, f - 11110100, p - 11110000 et - 11100000 octets. Ou sinon, dans les codes ASCII, le mot "digit" = 1111 0110 1110 1000 1111 0100 1111 0000 1110 0000
avec une décomposition en tétrades (4 chiffres chacune). Ainsi, le codage du mot «chiffre» NL nécessite 10 mots de code du (7, 4) code de Hamming. Les tétrades représentent les bits d'information des mots de message. Ces mots d'information (tétrades) sont convertis en mots de code (7 bits chacun) avant d'être envoyés au canal du réseau de communication. Cela se fait par multiplication de matrice vectorielle: le mot d'information par la matrice génératrice. Le paiement par commodité est très coûteux et prend du temps, mais tout fonctionne automatiquement et, surtout, le message est protégé des erreurs.
La matrice de génération du code de Hamming (7, 4) ou du générateur de mot de code est obtenue en écrivant les vecteurs de base du code et en les combinant dans une matrice. Cela découle du théorème de l'algèbre linéaire: tout vecteur d'un espace (sous-espace) est une combinaison linéaire de vecteurs de base, i.e. linéairement indépendant dans cet espace. C'est exactement ce qui est nécessaire - pour générer des vecteurs (mots de code de 7 bits) à partir de ceux de 4 bits d'informations.
La matrice génératrice du code de Hamming (7, 4, 3) ou du générateur de mot de code a la forme:
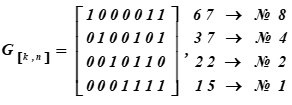
A droite se trouvent les représentations décimales des mots de code de la base du sous-espace et leurs numéros de série dans le tableau K
n ° i lignes de la matrice sont les mots du code qui sont à la base du sous-espace vectoriel.
Un exemple de codage de mots de messages d'information (la matrice génératrice du code est construite à partir des vecteurs de base et correspond à la partie de la table K). Dans la table des codes ASCII, nous prenons la lettre q = <1111 0110>.
Les mots d'information du message ressemblent à:
...
Ce sont la moitié du caractère (c). Pour le code (7, 4) défini précédemment, il est nécessaire de trouver les mots de code correspondant au mot-message d'information (c) de 8 caractères sous la forme:
...
Pour transformer ce message-lettre (q) en mots de code u, chaque moitié du message-lettre i est multipliée par la matrice génératrice G [k, n] du code (matrice pour le tableau K):
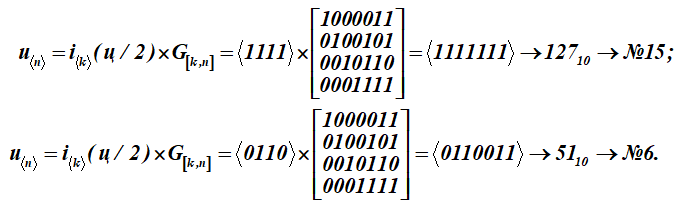
Nous avons obtenu deux mots de code avec les numéros de série 15 et 6.
Afficher formation détaillée du résultat inférieur n ° 6 - un mot de code (multiplication de la ligne du mot d'information par les colonnes de la matrice génératrice); sommation sur (mod2)
<0110> ∙ <1000> = 0 ∙ 1 + 1 ∙ 0 + 1 ∙ 0 + 0 ∙ 0 = 0 (mod2);
<0110> ∙ <0100> = 0 ∙ 0 + 1 ∙ 1 + 1 ∙ 0 + 0 ∙ 0 = 1 (mod2);
<0110> ∙ <0010> = 0 ∙ 0 + 1 ∙ 0 + 1 ∙ 1 + 0 ∙ 0 = 1 (mod2);
<0110> ∙ <0001> = 0 ∙ 0 + 1 ∙ 0 + 1 ∙ 0 + 0 ∙ 1 = 0 (mod2);
<0110> ∙ <0111> = 0 ∙ 0 + 1 ∙ 1 + 1 ∙ 1 + 0 ∙ 1 = 0 (mod2);
<0110> ∙ <1011>= 0 ∙ 1 + 1 ∙ 0 + 1 ∙ 1 + 0 ∙ 1 = 1 (mod2);
<0110> ∙ <1101> = 0 ∙ 1 + 1 ∙ 1 + 1 ∙ 0 + 0 ∙ 1 = 1 (mod2).
Reçus à la suite de la multiplication des quinzième et sixième mots du tableau K. Les quatre premiers bits de ces mots de code (résultats de multiplication) représentent des mots d'information. Ils ressemblent à:, (dans le tableau ASCII, ce n'est que la moitié de la lettre t). Pour la matrice de codage, un ensemble de mots numérotés: 1, 2, 4, 8 sont sélectionnés comme vecteurs de base dans le tableau K. Dans le tableau, ils sont mis en évidence par remplissage. Alors pour cette table K la matrice de codage recevra la forme G [k, n].
À la suite de la multiplication, 15 et 6 mots de la table de codes K ont été obtenus.
Application de code. Décodeur
Le décodeur est situé du côté de réception du canal où se trouve le récepteur du message. Le but du décodeur est de fournir au destinataire le message transmis sous la forme dans laquelle il existait chez l'expéditeur au moment de l'envoi, c'est-à-dire le destinataire peut utiliser le texte et utiliser les informations qu'il contient pour son travail ultérieur.
La tâche principale du décodeur est de vérifier si le mot reçu (7 bits) est celui qui a été envoyé du côté émetteur, si le mot contient des erreurs. Pour résoudre ce problème, pour chaque mot reçu par le décodeur, en le multipliant par la matrice de contrôle H [nk, n], un syndrome de vecteur court S (3 bits) est calculé.
Pour les mots qui sont du code, c'est-à-dire ne contiennent pas d'erreurs, le syndrome prend toujours une valeur nulle S = <000>. Pour un mot avec une erreur, le syndrome n'est pas nul S ≠ 0. La valeur du syndrome permet de détecter et localiser la position de l'erreur jusqu'à un bit dans le mot reçu côté réception, et le décodeur peut changer la valeur de ce bit. Dans la matrice de contrôle du code, le décodeur trouve une colonne qui correspond à la valeur du syndrome, et le nombre ordinal de cette colonne est égal au bit déformé par l'erreur. Après cela, pour les codes binaires, le décodeur change ce bit - remplacez-le simplement par la valeur opposée, c'est-à-dire qu'un est remplacé par zéro et zéro est remplacé par un.
Le code en question est systématiquec'est-à-dire que les symboles du mot d'information sont placés dans une rangée dans les bits les plus significatifs du mot de code. Les mots d'information sont restaurés en supprimant simplement les bits les moins significatifs (de contrôle), dont le nombre est connu. Ensuite, une table de codes ASCII est utilisée dans l'ordre inverse: l'entrée est des séquences binaires d'information, et la sortie est les lettres de l'alphabet en langage naturel. Ainsi, le code (7, 4) est systématique, groupé, linéaire, bloc, binaire .
La base du décodeur est formée par la matrice de contrôle H [nk, n], qui contient le nombre de lignes égal au nombre de symboles de contrôle, et toutes les colonnes possibles, à l'exception de zéro, colonnes de trois caractères... La matrice de contrôle de parité est construite à partir des mots de la table K, ils sont choisis orthogonaux à la matrice de codage, c'est-à-dire leur produit est la matrice zéro. La matrice de contrôle prend la forme suivante dans les opérations de multiplication, elle est transposée. Pour un exemple spécifique, la matrice de contrôle H [nk, n] est donnée ci-dessous:
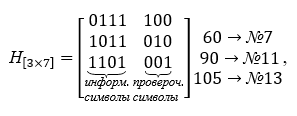



On voit que le produit de la matrice génératrice et de la matrice de contrôle aboutit à une matrice nulle.
Exemple 2. Décodage d'un mot du code de Hamming sans erreur (e <7> = <0000000>).
Soit à la réception du canal reçu les mots # 7 → 60 et # 13 → 105 de la table K,
u <7> + e <7> = <0 1 1 1 1 0 0> + <0 0 0 0 0 0 0>,
là où il n'y a pas d'erreur, c'est-à-dire qu'il a la forme e <7> = <0 0 0 0 0 0 0>.

En conséquence, le syndrome calculé a une valeur nulle, ce qui confirme l'absence d'erreur dans les mots du code.
Exemple 3 . Détection d'une erreur dans un mot reçu à l'extrémité de réception du canal (Tableau K).
A) Qu'il soit nécessaire de transmettre le 7ème mot de code, c'est-à-dire
u <7> = <0 1 1 1 1 0 0> et dans un tiers à partir de la gauche du mot, une erreur a été commise. Puis il est additionné mod2 avec le 7ème mot de code transmis sur le canal de communication
u <7> + <7> = <0 1 1 1 1 0 0> + <0 0 1 0 0 0 0> = <0 1 0 1 1 0 0>,
où l'erreur a la forme e <7> = <0 0 1 0 0 0 0>.
L'établissement du fait de distorsion du mot de code est effectué en multipliant le mot déformé reçu par la matrice de contrôle du code. Le résultat de cette multiplication sera un vecteurappelé syndrome du mot de code.
Effectuons une telle multiplication pour nos données originales (7ème vecteur avec une erreur).

A la suite d'une telle multiplication, à l'extrémité réceptrice du canal, un syndrome vectoriel S <nk> a été obtenu, dont la dimension est (n - k). Si le syndrome S <3> = <0,0,0> est nul, alors on conclut que le mot reçu du côté récepteur appartient au code C et est transmis sans distorsion. Si le syndrome n'est pas égal à zéro S <3> ≠ <0,0,0>, alors sa valeur indique la présence d'une erreur et sa place dans le mot. Le bit déformé correspond au numéro de la position de colonne de la matrice [nk, n], qui coïncide avec le syndrome. Après cela, le bit déformé est corrigé et le mot reçu est ensuite traité par le décodeur. En pratique, un syndrome est immédiatement calculé pour chaque mot accepté, et s'il y a une erreur, il est automatiquement éliminé.
Ainsi, lors des calculs, le syndrome S = <110> est le même pour les deux mots. Nous regardons la matrice de contrôle et trouvons la colonne qui correspond au syndrome. Ceci est la troisième colonne à partir de la gauche. Par conséquent, l'erreur a été commise dans le troisième chiffre à partir de la gauche, qui coïncide avec les conditions de l'exemple. Ce troisième bit est changé à la valeur opposée et nous avons renvoyé les mots reçus par le décodeur sous forme de code. L'erreur a été trouvée et corrigée.
C'est tout, c'est ainsi que le code Hamming classique (7, 4) fonctionne et fonctionne.
De nombreuses modifications et mises à niveau de ce code ne sont pas prises en compte ici, car ce ne sont pas elles qui sont importantes, mais ces idées et leurs implémentations qui ont radicalement changé la théorie du codage et, par conséquent, les systèmes de communication, l'échange d'informations, les systèmes de contrôle automatisés.
Conclusion
Le papier examine les principales dispositions et tâches de la sécurité de l'information, nomme les théories conçues pour résoudre ces problèmes.
La tâche de protéger l'interaction informationnelle des sujets et des objets contre les erreurs environnementales et les actions d'un intrus appartient à la codologie.
Le code de Hamming (7, 4), qui a marqué le début d'une nouvelle direction dans la théorie du codage, est la synthèse des codes correcteurs.
L'application de méthodes mathématiques rigoureuses utilisées dans la synthèse de code est présentée.
Des exemples sont donnés pour illustrer l'efficacité du code.
Littérature
Peterson W., Weldon E. Codes de correction d'erreur: Trans. de l'anglais M .: Mir, 1976, 594 p.
Bleihut R. Théorie et pratique des codes de contrôle d'erreur. Traduit de l'anglais. M.: Mir, 1986, 576 p.