Les mathématiques à distance sociale sont une leçon de géométrie

Le défi de rouvrir en toute sécurité des bureaux, des écoles et d'autres espaces publics tout en gardant les gens à un mètre et demi de distance se résume à une question que les mathématiciens étudient depuis des siècles.

Il peut sembler qu'un sujet tel que l' emballage des sphères ne plaira qu'aux mathématiciens. Qui d'autre serait intéressé à rechercher les moyens les plus efficaces de placer des cercles sur un plan ou des sphères dans l'espace?



Cependant, aujourd'hui, des millions de personnes dans le monde réfléchissent exactement à cette tâche.



Déterminer comment ouvrir en toute sécurité les bâtiments et les espaces publics tout en maintenant une distance sociale est, en particulier, un exercice de géométrie. Si chaque personne doit être à au moins un mètre et demi des autres personnes, alors pour calculer le nombre de personnes pouvant s'asseoir dans la salle de classe ou la salle à manger, vous devez placer des cercles qui ne se chevauchent pas sur le plan d'étage.







Naturellement, pour lutter contre le coronavirus, beaucoup plus de problèmes doivent être résolus que celui-ci géométrique. Cependant, l'empilement de cercles et de sphères joue un rôle à cet égard - tout comme la modélisation des structures cristallines en chimie et les espaces de messages abstraits en théorie de l'information. Cette tâche, en apparence simple dans sa description, a occupé l'esprit des plus grands mathématiciens de l'histoire, et les recherches les plus intéressantes dans ce domaine sont menées aujourd'hui, en particulier, dans des dimensions supérieures. Par exemple, des mathématiciens ont récemment trouvé le meilleur moyen de regrouper dans des espaces de 8 et 24 dimensions - une technique nécessaire pour optimiser les codes de correction d'erreur utilisés à la fois dans les téléphones portables et dans la communication avec les sondes spatiales. Jetons donc un coup d'œil à certaines des complications inattendues qui surviennent lorsque nous essayons de remplir un espace avec le formulaire le plus simple.



Que vous emballiez des oranges dans des boîtes au travail ou que vous installiez des étudiants en toute sécurité avec une distance sociale, la taille et la forme de votre contenant sont essentielles à votre tâche. Cependant, pour la plupart des mathématiciens, la théorie de l'empilement de sphères consiste à remplir l'espace entier. En deux dimensions, cela signifie recouvrir le plan de cercles disjoints de même taille.



Voici un exemple de cercles d'emballage sur un avion. Cela ressemble à une vue de dessus d'un paquet de soda:







Vous pouvez imaginer comment ce motif se répète dans toutes les directions, comme une tuile qui a été pavée avec un avion. De petits espaces entre les cercles indiquent que le plan n'est pas complètement rempli, mais dans le cas des cercles d'emballage, cela devrait être prévu. Nous nous intéressons au pourcentage de l'avion couvert. Ce sera la "densité de remplissage" de la méthode particulière.



La méthode ci-dessus est appelée emballage carré, et pour une bonne raison - les centres des cercles peuvent être représentés comme les sommets des carrés.







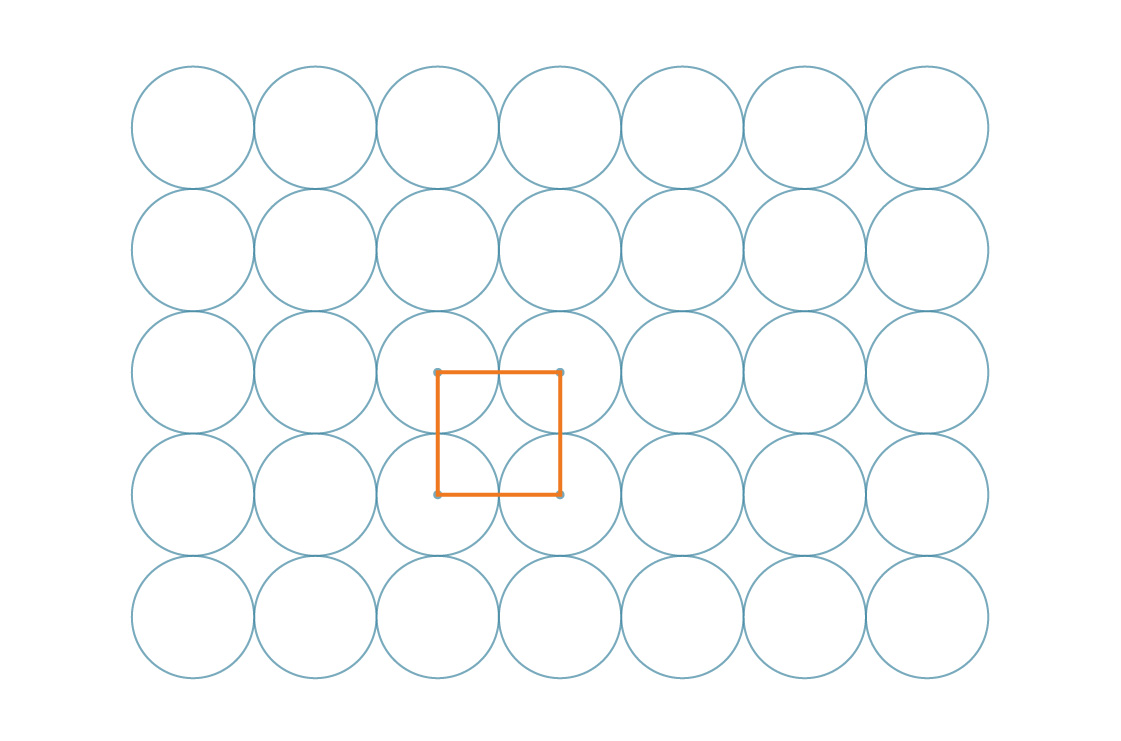
Et en fait, ces carrés eux-mêmes tuent le plan:







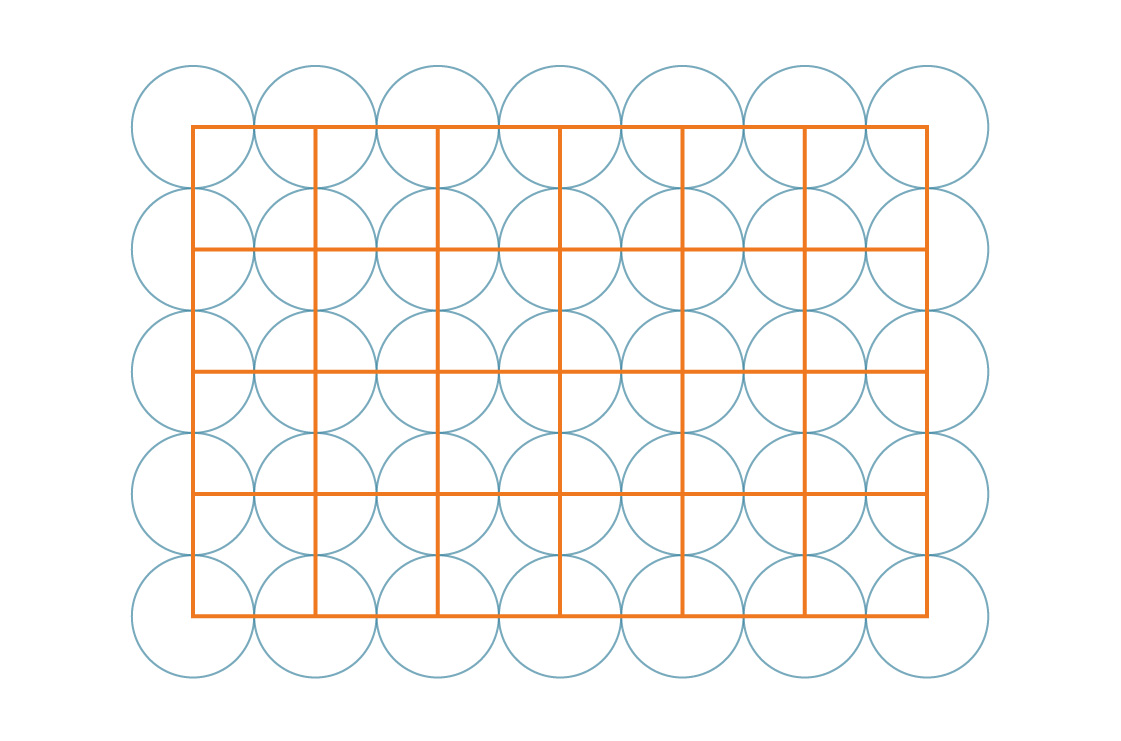
Notre tâche est facilitée par la symétrie du motif. Puisque ces carrés couvrent le plan entier de manière périodique, le pourcentage du plan couvert par les cercles est le même que le pourcentage du carré couvert par les cercles. Regardons l'un de ces carrés.







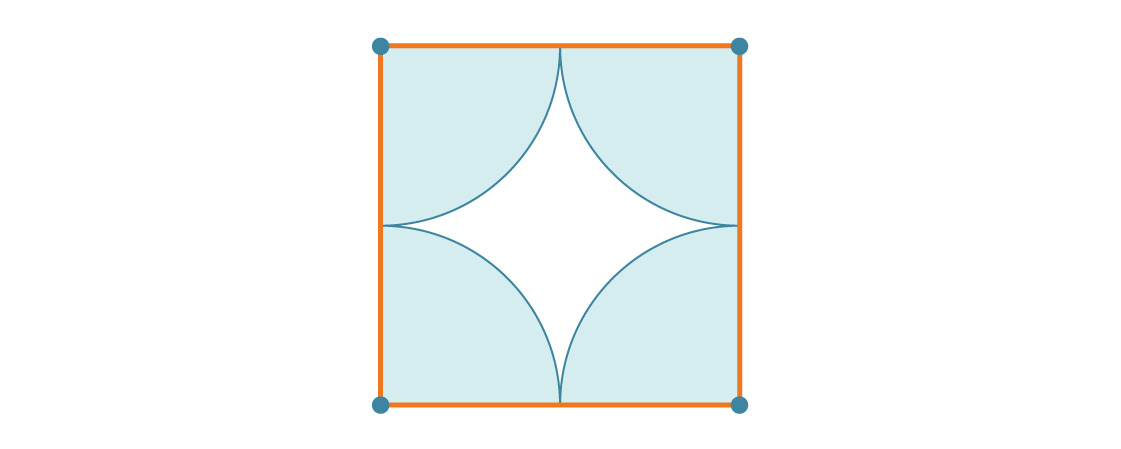
Disons que le rayon du cercle est r. Cela signifie que la longueur du côté du carré est de 2r. À chacun des sommets du carré, il y a un quart de cercle, donc le pourcentage de couverture de chaque carré est simplement égal au rapport de l'aire d'un cercle complet à l'aire d'un carré complet:

$$

$$\frac{\pi r^2}{(2r)^2} = \frac{\pi r^2}{4r^2} = \frac{\pi }{4} \approx 0,7854$$

Chaque carré est couvert à environ 78,54% de cercles, donc compte tenu du carrelage de l'avion, tout est couvert à environ 78,54% de cercles. C'est la densité de l'emballage carré. Notez que le rayon r a disparu de la réponse. Et cela a du sens: quelle que soit la taille des cercles, il y aura toujours quatre quarts de cercle dans un carré.



Si vous avez essayé de plier les canettes de soda sur le côté comme ceci, et qu'elles glissent et remplissent les espaces, vous savez qu'il existe une autre façon de tasser les cercles sur un plan:







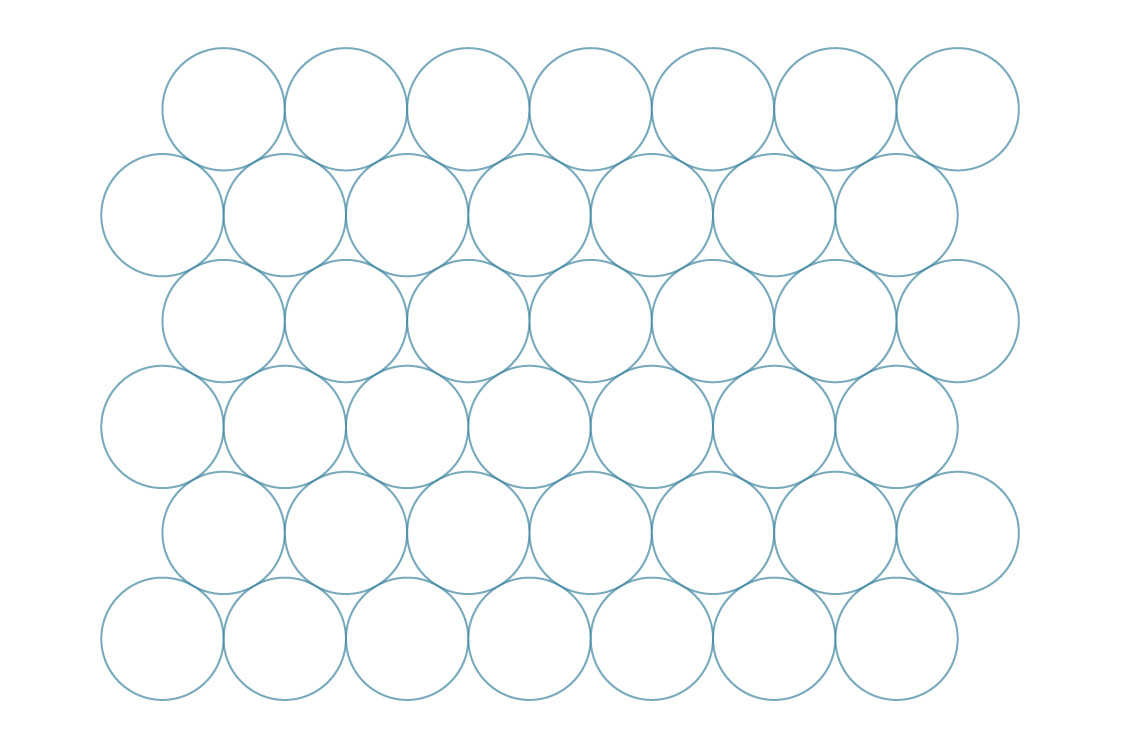
adoptons une approche similaire à la précédente et imaginons que les centres des cercles forment dans ce cas des hexagones réguliers ...







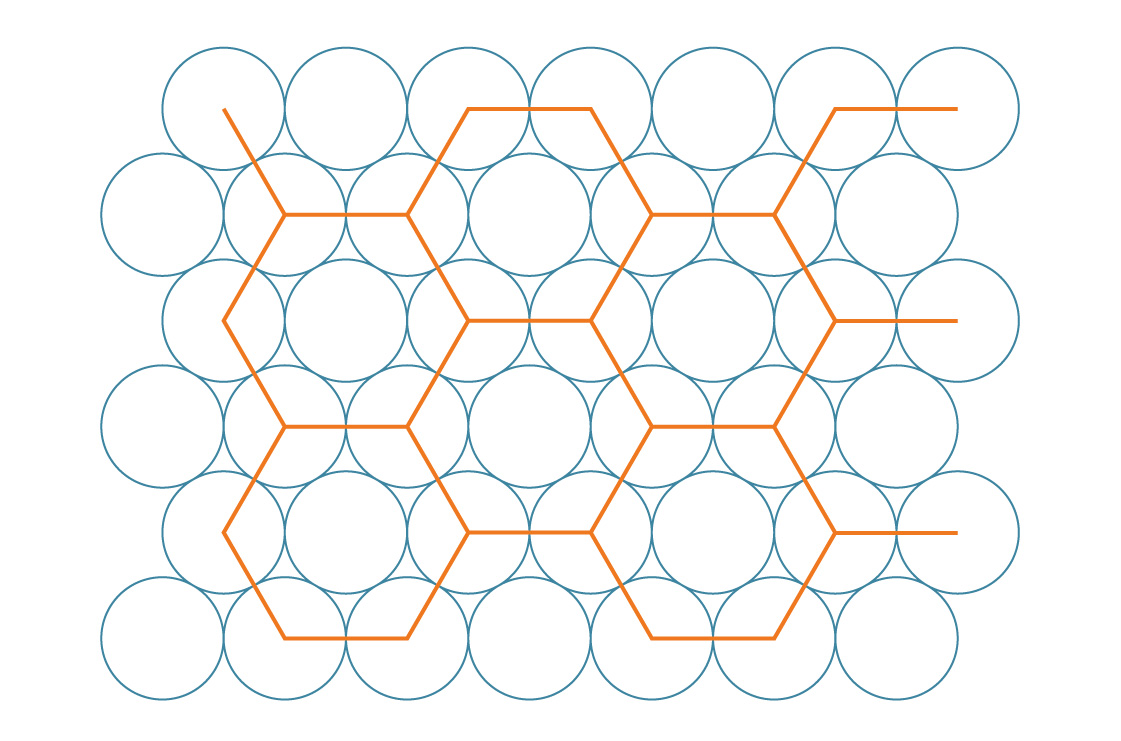
Nous appelons cet emballage hexagonal. Il semble que cette méthode comble les lacunes plus efficacement que le carré. Pour vérifier cela, comparons leurs densités d'emballage. Les hexagones, comme les carrés, recouvrent complètement le plan, nous pouvons donc déterminer la densité de cette méthode en analysant un seul hexagone.







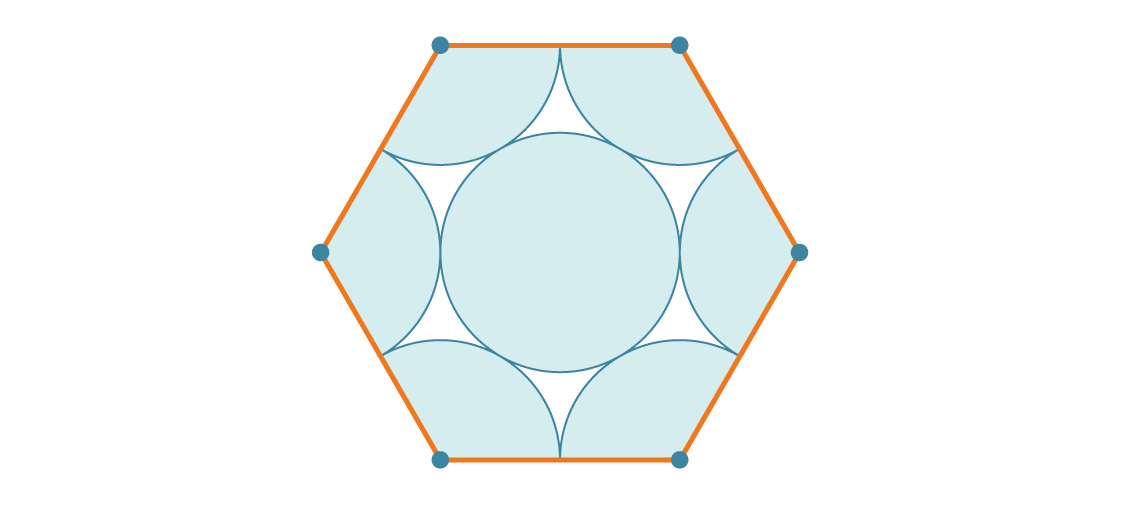
Quelle partie de l'hexagone est recouverte de cercles? Puisqu'un hexagone régulier a un angle intérieur de 120 °, chaque coin a un tiers de cercle. Il en résulte deux cercles complets et le cercle du milieu passe en troisième. Par conséquent, chaque hexagone est couvert par trois cercles. Si le rayon de chaque cercle est r, alors l'aire est 3πr².







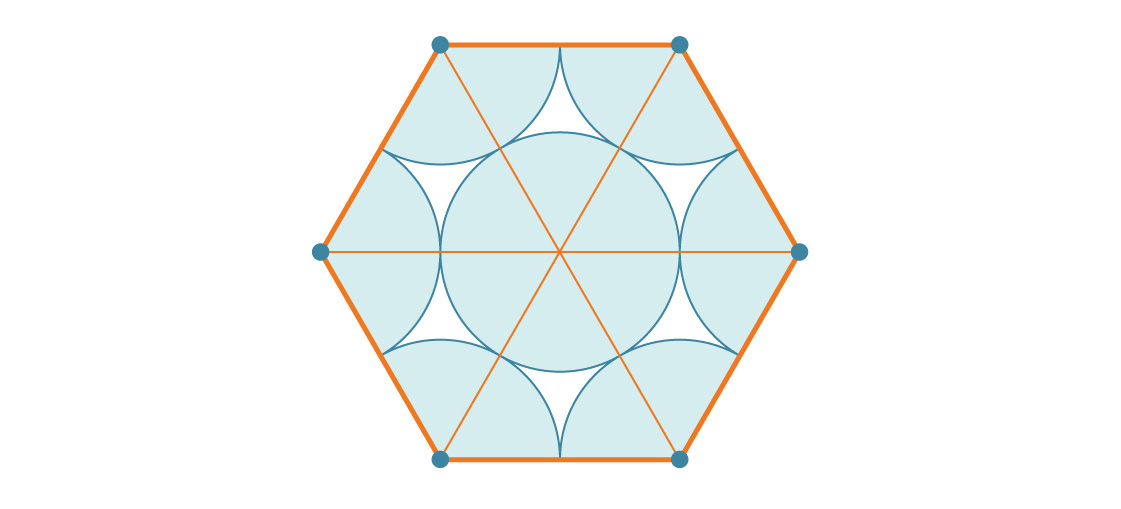
Comment cela se compare-t-il à l'aire d'un hexagone? Un hexagone de longueur de côté s est constitué de six triangles équilatéraux de longueur de côté s, chacun étant s ² √3 / 4. Par conséquent, l'aire de l'hexagone est 6 * s ² √3 / 4 = 6 s ² √3 / 4. Puisque la longueur de côté de notre hexagone est 2r, sa surface est:

$$

$$\frac{6 s^2 \sqrt3}{4} = \frac{6 (2r)^2 \sqrt3}{4} = \frac{24 r^2 \sqrt3}{4} = 6 r^2 \sqrt3$$

Vous pouvez maintenant calculer le pourcentage de l'hexagone couvert par les cercles (en divisant l'aire des six cercles par l'aire de l'hexagone):

$$

$$\frac{3 \pi r^2}{6 r^2 \sqrt3} = \frac{3 \pi}{6 \sqrt3} = \frac{\pi}{2 \sqrt3} \approx 0,9069$$

Chaque hexagone est couvert à environ 90,69% de cercles, donc cet emballage sera beaucoup plus efficace qu'un carré. Remarquez comment le rayon du cercle disparaît à nouveau comme prévu. En fait, il n'y a pas d'emballage plus efficace.



Mais il n'a pas été facile de le prouver. Des mathématiciens célèbres tels que Joseph Louis Lagrange et Karl Friedrich Gauss ont commencé à y travailler à la fin du XVIIIe et au début du XIXe siècle, mais le problème n'a été complètement résolu que dans les années 1940, en traitant soigneusement tous les arrangements possibles - périodiques et non périodiques. Le fait qu'il ait fallu tant de temps pour résoudre le problème en deux dimensions, où tout est assez facile à imaginer, peut servir d'avertissement à ce qui nous attend dans les dimensions supérieures.



Emballer des sphères en trois dimensions est une tâche beaucoup plus difficile, même si elle présente certaines similitudes avec son cousin bidimensionnel. Par exemple, les emballages bidimensionnels que nous avons considérés sont constitués d'une seule couche.







Pour un paquet carré, nous plaçons chaque couche au-dessus de la précédente.







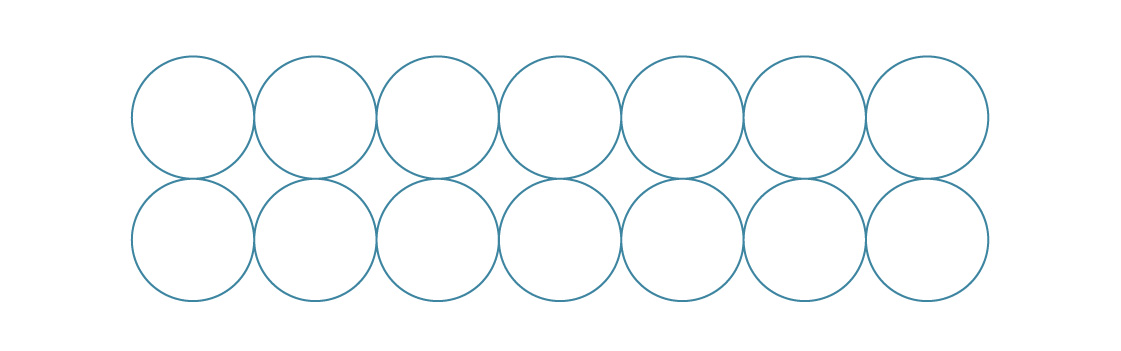
Pour l'emballage hexagonal, nous avons placé de nouvelles couches entre les précédentes.







Différents emballages sont obtenus en fonction de la façon dont nous combinons des copies de différentes couches.



En trois dimensions, cet agencement de couches les unes sur les autres crée des emballages fondamentalement différents.







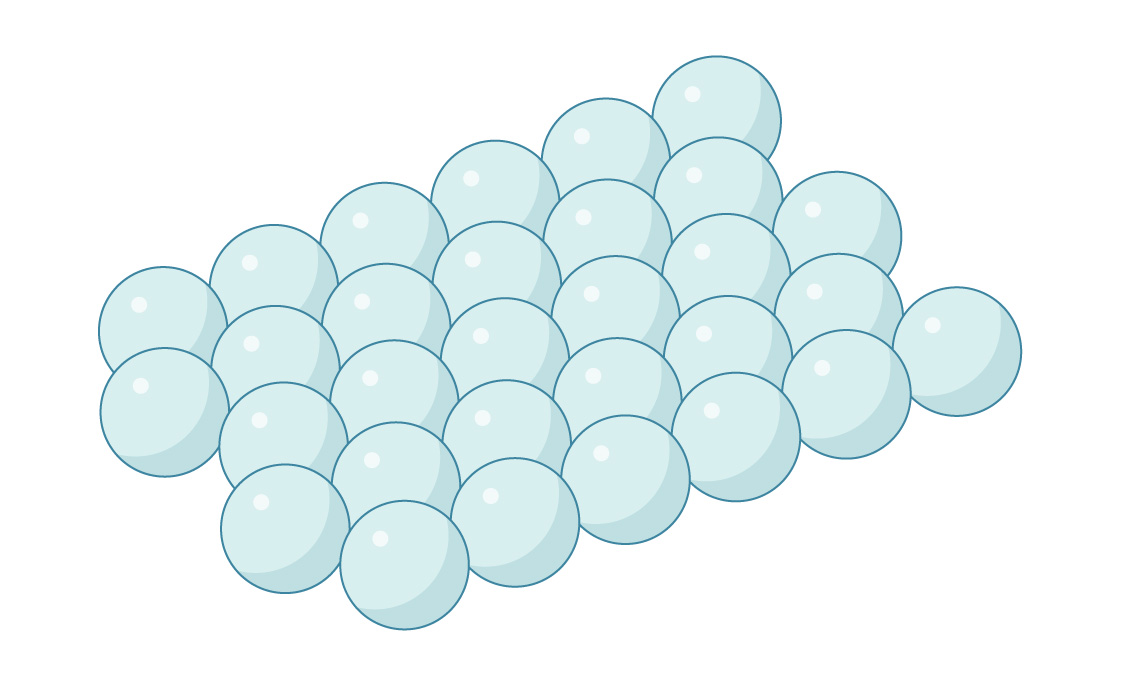
Il s'agit d'une couche de sphères emballées de manière hexagonale, comme le suggère notre emballage optimal de cercles sur un plan. De même, vous pouvez placer la deuxième couche au-dessus de la première en plaçant des sphères dans les espaces entre les sphères inférieures.







Mais en trois dimensions, la géométrie se complique un peu. Dans chaque couche de sphères, la distance entre les espaces adjacents s'avère inférieure à la distance entre les centres des sphères. Par conséquent, vous ne pouvez pas coller une sphère dans chaque espace - elles se croiseraient. Par conséquent, les espaces dans les deux couches s'alignent pour créer des canaux qui traversent le package.







Il existe deux façons de placer la troisième couche. Vous pouvez aligner les espaces avec ceux du bas et laisser les canaux ouverts. Voici une vue latérale de cet agencement:







Afin de garder les canaux ouverts, vous devez placer les sphères dans la troisième couche juste au-dessus des sphères de la première couche. Cet agencement de sphères s'appelle un "emballage dense hexagonal" (silo), et si vous le regardez d'en haut, vous pouvez voir des espaces ouverts qui le traversent.







Une autre option pour placer la troisième couche consiste à fermer les canaux. Les sphères de la troisième couche sont placées directement au-dessus des interstices de la première: c'est







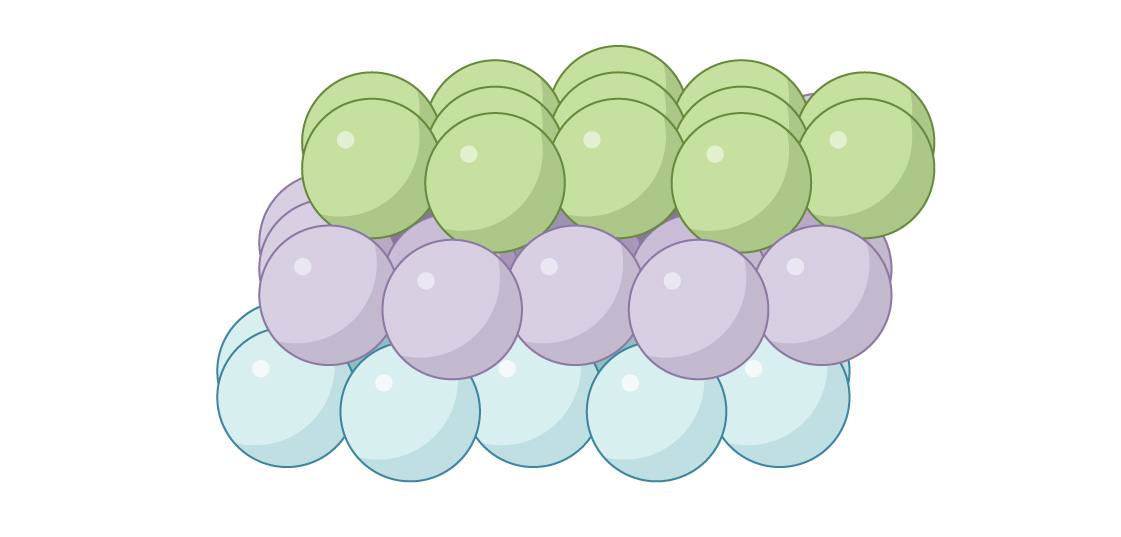
ce qu'on appelle «cubique à faces centrées» (FCC) ou «cubic close packing». Vu d'en haut, il n'y aura pas de lacunes.







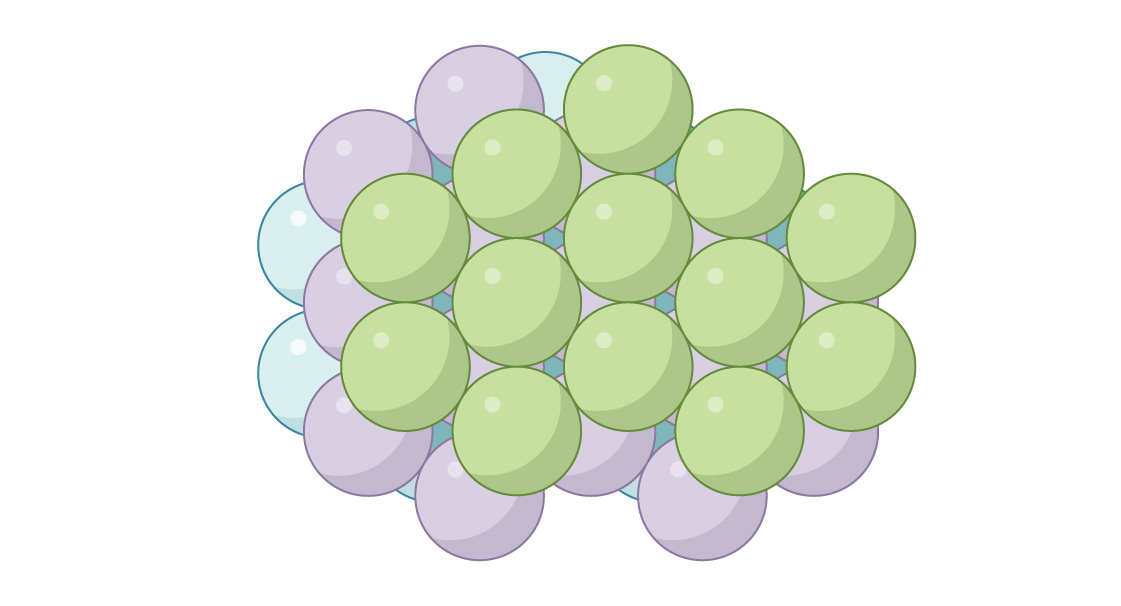
Ces deux arrangements similaires mais fondamentalement différents surviennent en chimie, décrivant l'arrangement des atomes dans différents matériaux. Par exemple, dans les métaux tels que l'argent et l'or, la structure a la forme de HA, et dans les métaux tels que le zinc et le titane - les silos. Chacune des deux méthodes vous permet de remplir l'espace avec des sphères. Dans la méthode du silo, dans une couche sur deux, les sphères sont situées exactement de la même manière et dans le GK - dans chaque troisième. Vous pouvez créer un nombre infini de packages différents en combinant ces deux méthodes, mais il est intéressant que silo et GK donnent un emballage optimal! Leur densité de tassement n'est pas seulement la même, π 3√2 ≈ 0,7405 est le tassement le plus dense possible dans un espace tridimensionnel. Le célèbre mathématicien et astronome Johannes Kepler a suggéré cela en 1611, mais preuve complèteseul le mathématicien Thomas Hales a pu en déduire en 1998.







Il y a plus de place dans l'espace 3D et nous avons plus de moyens pour emballer efficacement les sphères. Lorsque vous ajoutez des dimensions, la complexité de l'emballage ne fait qu'augmenter - il y a plus d'espace, plus d'options et c'est plus difficile à imaginer. De plus, les sphères deviennent plus petites dans des dimensions plus élevées!







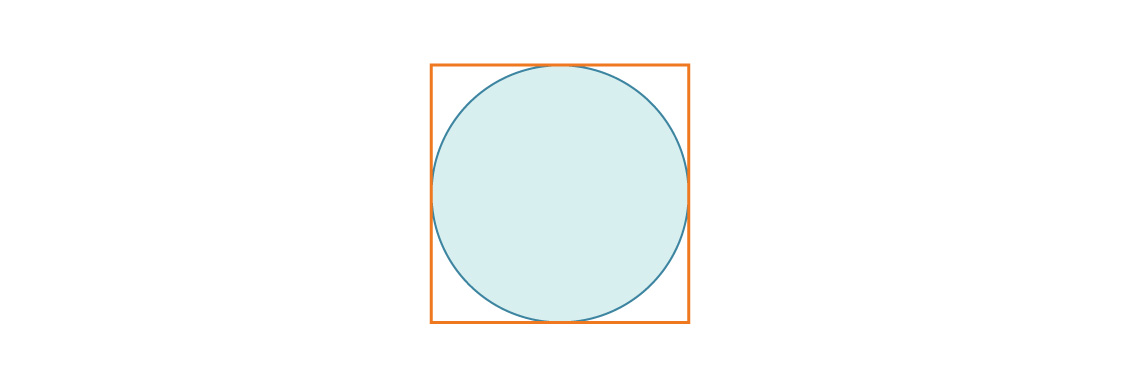
Considérons un cercle inscrit dans un carré de longueur de côté 1.



Le rayon du cercle est r = 1/2, donc le rapport de l'aire du cercle à l'aire du carré est:

$$

$$\frac{\pi r^2}{s^2} = \frac{\pi (\frac{1}{2})^2}{1^2} = \frac{\pi }{4} \approx 0,7854$$

Qui est également égale à la densité de tassement du carré en deux dimensions.



Considérons maintenant le volume d'une sphère inscrite dans un cube unité.







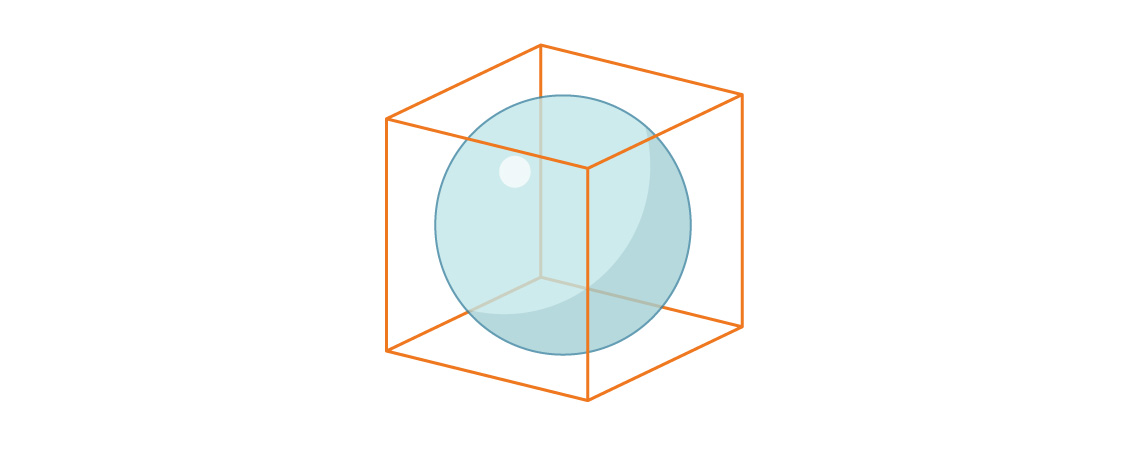
Le rayon de la sphère est à nouveau égal à r = 1/2, donc le rapport du volume de la sphère au volume du cube est:

$$

$$\frac{\frac{4}{3}\pi r^3}{s^3} = \frac{\frac{4}{3}\pi (\frac{1}{2})^3}{1^3} = \frac{4}{3}\pi (\frac{1}{8}) = \frac{\pi}{6} \approx 0,5236$$

Notez que la proportion du cube occupée par la sphère inscrite en trois dimensions est inférieure à la proportion du carré occupée par le cercle inscrit en deux dimensions. Ce schéma se poursuit: avec des dimensions croissantes, ce rapport diminue. Au fur et à mesure que n grandit, les sphères à n dimensions occupent de moins en moins d'espace à n dimensions.



Cela peut être montré en utilisant l'algèbre, mais cela peut aussi être compris si vous pensez aux angles. Dans n'importe quelle dimension, une sphère à n dimensions peut être inscrite dans un cube à n dimensions. La sphère touche les bords du cube mais n'atteint pas les coins, il y a donc une région autour de chaque coin qui est à l'intérieur du cube mais à l'extérieur de la sphère. Cependant, une boîte à n dimensions aura 2 ⁿangles, c'est-à-dire qu'avec une augmentation de n, le nombre de zones non couvertes par la sphère augmente de façon exponentielle. De plus, la distance entre les coins et la sphère augmente également. Cela signifie qu'à long terme, l'espace à l'intérieur du cube à n dimensions, mais à l'extérieur de la sphère à n dimensions, écrasera simplement l'espace occupé par la sphère.



Si la contraction des sphères vous semble assez étrange, alors les mathématiciens impliqués dans le conditionnement des sphères ont remarqué quelque chose d'encore plus inattendu dans les dimensions 8 et 24. Dans ces dimensions, les sphères rétrécissent juste assez pour pouvoir combler les vides entre les nouvelles sphères, ce qui donne un emballage ultra-dense dans ces dimensions ... On a émis une hypothèse sur l'optimalité de ces méthodes spéciales, mais elle n'était connue exactement qu'en 2016, lorsque Marina Vyazovskaya a prouvé ce théorèmepour un espace à 8 dimensions. Une semaine plus tard, Vyazovskaya et ses assistants ont développé sa méthode pour prouver le cas dans un espace à 24 dimensions.



Il découle du travail de Vyazovskaya que nous connaissons maintenant les moyens les plus efficaces pour emballer des sphères dans les dimensions 1, 2, 3, 8 et 24. Mais dans d'autres dimensions, il reste encore beaucoup de travail à faire. Alors sortez les oranges et les canettes de soda et commencez à expérimenter. C'est peut-être vous qui pouvez combler les lacunes importantes.

Des exercices

1. Disons que nous avons commencé à emballer le plan de coordonnées comme indiqué dans les images ci-dessous. Le centre du cercle inférieur gauche est situé au point (0, 0) et le centre du cercle inférieur droit est au point (2, 0).







Où est le centre du troisième cercle?



2. Ci-dessous se trouve le début de l'empilement "cubique simple" de sphères. Quelle est la densité de remplissage d'un tel schéma?







3. Voici le début de l'emballage de l'avion en octogones réguliers.







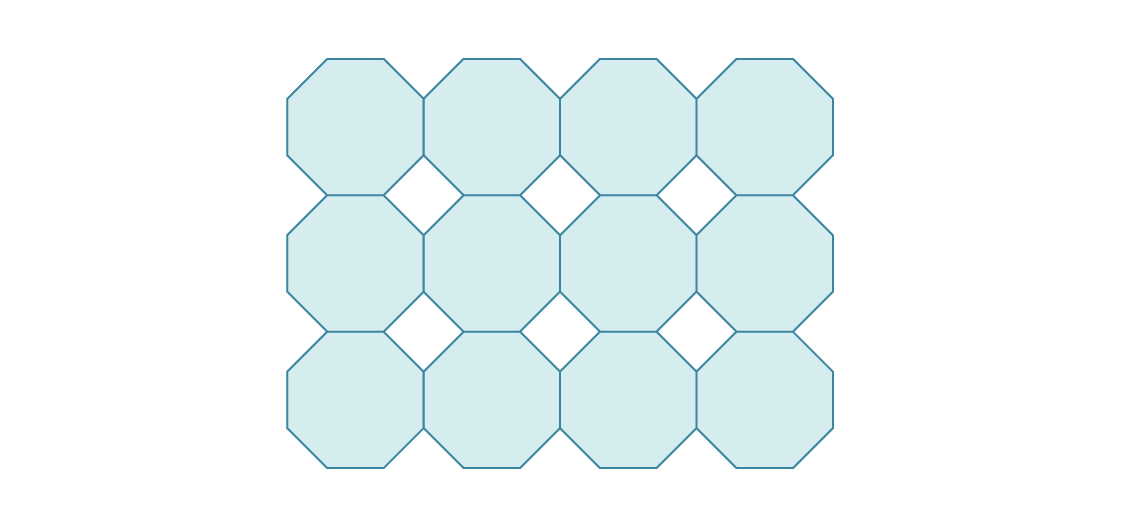
Quelle est la densité d'un tel emballage?

Réponses

Voir également:

• " Google lance Sodar, un outil de RA pour afficher la distance sociale "
• "Une méta-étude révèle l'efficacité des masques et de la distanciation contre le SRAS-CoV-2 (COVID-19) "
• " COVID-19: modèle de prévision paramétrique épidémique "