De la capacité à traiter d'énormes quantités d'informations et à utiliser beaucoup plus efficacement les algorithmes d'apprentissage automatique, aux algorithmes de modélisation quantique qui peuvent améliorer les calculs (à la fois qualitativement et quantitativement) pour la conception de nouveaux médicaments, la prédiction de la structure des protéines, l'analyse de divers processus dans un organisme biologique, et etc. Ces perspectives époustouflantes font aujourd'hui l'objet d'un battage médiatique écrasant, ce qui signifie qu'il est important de mettre en évidence les mises en garde et les défis de cette nouvelle technologie.
Avertissement: La revue est basée sur un article d'un groupe de chercheurs européens du Royaume-Uni et de Suisse (Carlos Outeiral, Martin Strahm, Jiye Shi, Garrett M. Morris, Simon C. Benjamin, Charlotte M. Deane. "Les perspectives de l'informatique quantique en biologie moléculaire computationnelle", WIREs Computational Molecular Science publié par Wiley Periodicals LLC, 2020). Les parties les plus difficiles de l'article liées aux modèles mathématiques sophistiqués ne seront pas incluses dans la revue. Mais le matériel est initialement complexe et le lecteur doit avoir des connaissances en mathématiques et en physique quantique.
Mais si vous avez l'intention de commencer à étudier l'application des technologies quantiques à la bioinformatique, il est suggéré d'écouter un court discours de Viktor Sokolov, chercheur principal chez M&S Decisions, qui décrit certains problèmes modernes de la modélisation des médicaments:
introduction
Depuis l'avènement du calcul haute performance, des algorithmes et des modèles mathématiques ont été utilisés pour résoudre des problèmes en sciences biologiques - de l'étude de la complexité du génome humain à la modélisation du comportement des biomolécules. Les méthodes informatiques sont régulièrement utilisées aujourd'hui pour analyser et extraire des informations importantes d'expériences biologiques, ainsi que pour prédire le comportement d'objets et de systèmes biologiques. En fait, 10 des 25 articles scientifiques les plus cités traitent d'algorithmes de calcul utilisés en biologie [voir p. ici ], y compris la modélisation quantique [ ici , ici , ici et ici ], l'alignement de séquence [ ici , ici etici ], la génétique computationnelle [voir. ici ] et la diffraction des rayons X dans le traitement des données [cf. ici et ici ].
Malgré ces progrès, de nombreux problèmes de biologie restent insolubles du point de vue de leur solution à l'aide des technologies informatiques existantes. Les meilleurs algorithmes pour des tâches telles que la prédiction du repliement des protéines, le calcul de l'affinité de liaison d'un ligand à une macromolécule ou la recherche de l'alignement génomique optimal à grande échelle nécessitent des ressources informatiques qui vont au-delà même des supercalculateurs les plus puissants disponibles aujourd'hui.
La solution à ces problèmes peut résider dans un changement de paradigme dans la technologie informatique. Dans les années 1980 indépendamment, Richard Feynman [voir. ici ] et Yuri Manin [voir. here ] a suggéré d'utiliser des effets de mécanique quantique pour créer une nouvelle génération d'ordinateurs plus puissante.
La théorie quantique s'est avérée être une description très réussie de la réalité physique et a conduit, depuis sa création au début du XXe siècle, à des avancées telles que les lasers, les transistors et les microprocesseurs à semi-conducteurs. L'ordinateur quantique utilise les algorithmes les plus efficaces, utilisant des opérations qui ne sont pas possibles dans les machines classiques. Les processeurs quantiques ne fonctionnent pas plus vite que les ordinateurs classiques, mais ils fonctionnent d'une manière complètement différente, réalisant des accélérations sans précédent, évitant les calculs inutiles. Par exemple, le calcul de la fonction d'onde électronique totale de la molécule de médicament moyenne sur tout supercalculateur moderne utilisant des algorithmes conventionnels devrait prendre plus de temps que l'âge complet de notre univers [voir Réf. ici], alors que même un petit ordinateur quantique peut résoudre ce problème en quelques jours. Encouragés par une telle promesse d'avantage quantique, ingénieurs et scientifiques poursuivent leur quête d'un processeur quantique. Cependant, les difficultés techniques de fabrication, de gestion et de protection des systèmes quantiques sont incroyablement complexes et les premiers prototypes ne sont apparus que dans la dernière décennie.
Il est important de noter que les problèmes techniques de construction d'ordinateurs quantiques n'ont pas empêché le développement d'algorithmes de calcul quantique. Même en l'absence de matériel, les algorithmes peuvent être analysés mathématiquement, et l'avènement des simulateurs informatiques quantiques haute performance ainsi que des premiers prototypes au cours des dernières années a permis de poursuivre les recherches.
Plusieurs de ces algorithmes ont déjà montré des applications potentielles prometteuses en biologie. Par exemple, un algorithme d'estimation de la phase quantique permet de calculer des valeurs propres exponentiellement plus rapidement [voir. here ], qui peut être utilisé pour comprendre la corrélation à grande échelle entre les parties d'une protéine ou pour déterminer la centralité d'un graphe dans un réseau biologique. L'algorithme quantique de Harrow-Hasidim-Lloyd (HHL) [cf. here ] peut résoudre certains systèmes linéaires de façon exponentielle plus rapidement que n'importe quel algorithme classique connu, et peut également appliquer des méthodes d'apprentissage statistique avec un processus d'adaptation beaucoup plus rapide et la capacité de gérer de grandes quantités de données.
Les algorithmes d'optimisation quantique ont un large champ d'application dans le domaine du repliement des protéines et de la sélection des conformères, ainsi que dans les problèmes associés à la recherche de minima ou maxima [voir. ici ]. Enfin, une technologie a récemment été développée pour simuler des systèmes quantiques qui promettent, par exemple, de produire des prédictions précises des interactions médicament-récepteur [voir Réf. ici ] ou pour participer à l'étude et à la compréhension de processus complexes et de mécanismes chimiques tels que la photosynthèse [voir. ici ]. L'informatique quantique peut changer considérablement les méthodes de la biologie elle-même, comme l'informatique classique l'a fait en son temps.
Récentes revendications de suprématie quantique de Google [cf. ici], bien que contesté par IBM [cf. ici ], indiquent que l'ère de l'informatique quantique n'est pas loin. Les premiers processeurs à utiliser des effets quantiques pour effectuer des calculs impossibles pour la technologie informatique classique sont attendus dans la prochaine décennie [cf. ici ].
Dans cette revue, nous décomposerons les points clés où l'informatique quantique est prometteuse pour la biologie computationnelle. Ces revues analysent l'impact potentiel de l'informatique quantique dans divers domaines, y compris l'apprentissage automatique [cf. ici , ici et ici ], la chimie quantique [cf. ici , ici et ici ] et la synthèse des médicaments [voir.ici ]. Le rapport de l'atelier NIMH sur l'informatique quantique dans les sciences de la vie a également été récemment publié [voir p. ici ].
Dans cette revue, nous donnons d'abord une brève description de ce que l'on entend par calcul quantique et une brève introduction aux principes du traitement de l'information quantique. Nous abordons ensuite trois domaines principaux de la biologie computationnelle, où l'informatique quantique a déjà montré des développements algorithmiques prometteurs: les méthodes statistiques, les calculs de structure électronique et l'optimisation. Certains sujets importants seront laissés de côté, par exemple, les algorithmes de chaînes qui peuvent affecter l'analyse de séquence [voir. ici ], des algorithmes d'imagerie médicale [voir. ici ], algorithmes numériques pour les équations différentielles [ici ] et d'autres problèmes mathématiques ou méthodes d'analyse des réseaux biologiques [ ici ]. Enfin, nous discutons de l'impact potentiel de l'informatique quantique sur la biologie computationnelle à moyen et long terme.
1. Traitement de l'information quantique
Les ordinateurs quantiques promettent de résoudre des problèmes dans les sciences biologiques, tels que la prédiction des interactions protéine-ligand ou la compréhension de la co-évolution des acides aminés dans les protéines. Et ce n'est pas facile à résoudre, mais à le faire exponentiellement plus rapidement que vous ne pouvez l'imaginer avec n'importe quel ordinateur moderne. Cependant, ce changement de paradigme nécessite un changement fondamental dans notre réflexion: les ordinateurs quantiques sont très différents de leurs prédécesseurs classiques. Les phénomènes physiques qui sous-tendent l'avantage quantique sont souvent illogiques et contre-intuitifs, et l'utilisation d'un processeur quantique nécessite un changement fondamental dans notre compréhension de la programmation. Dans cette section, nous présentons les principes de l'information quantique et comment elle est traitée pour effectuer des calculs.
Nous expliquons comment l'information fonctionne différemment dans un système quantique, où elle est stockée en qubits, et comment cette information peut être manipulée à l'aide de portes quantiques. Comme les variables et les fonctions dans un langage de programmation, les qubits et les portes quantiques définissent les éléments de base de tout algorithme. Nous examinerons également pourquoi la création d'un ordinateur quantique est techniquement extrêmement difficile et ce qui peut être réalisé à l'aide des premiers prototypes attendus dans les années à venir. Cette introduction ne couvrira que les principaux points; pour une étude approfondie, lisez le livre de Nielsen et Chuang [ ici ].
1.1. Éléments d'algorithmes quantiques
1.1.1. Information quantique: une introduction au qubit
Le premier problème dans la représentation de l'informatique quantique est de comprendre comment il traite l'information. Dans un processeur quantique, les informations sont généralement stockées dans des qubits, qui sont l'analogue quantique des bits classiques. Un qubit est un système physique, comme un ion, limité par un champ magnétique [voir. ici ] ou un photon polarisé [voir. ici ], mais on en parle souvent dans l'abstrait. Comme le chat de Schrödinger, un qubit peut prendre non seulement les états 0 ou 1, mais aussi toute combinaison possible des deux états. Lorsqu'un qubit est observé directement, il ne sera plus dans une superposition qui s'effondre dans l'un des états possibles, tout comme le chat de Schrödinger est mort ou vivant après avoir ouvert la boîte [voir. ici]. Plus important encore, lorsque plusieurs qubits sont combinés, ils peuvent devenir corrélés et les interactions avec l'un d'entre eux ont des conséquences pour l'ensemble de l'état collectif. Le phénomène de corrélation entre plusieurs qubits, appelé intrication quantique, est une ressource fondamentale pour l'informatique quantique.
Dans l'information classique, l'unité fondamentale d'information est le bit, un système à deux états identifiables, souvent notés 0 et 1. L'analogue quantique, un qubit, est un système à deux états dont les états sont étiquetés | 0⟩ et | 1⟩. Nous utilisons la notation de Dirac, où | *⟩ identifie un état quantique. La principale différence entre les informations classiques et quantiques est qu'un qubit peut être dans n'importe quelle superposition d'états | 0⟩ et | 1⟩:
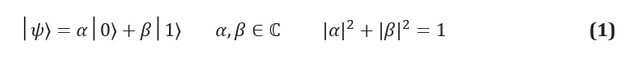
Les coefficients complexes α et β sont connus sous le nom d'amplitudes d'états, et ils sont liés à un autre concept clé de la mécanique quantique: l' effet de la dimension physique. Les qubits étant des systèmes physiques, vous pouvez toujours proposer un protocole pour mesurer leur état. Si, par exemple, les états | 0⟩ et | 1⟩ correspondent aux états du spin d'un électron dans un champ magnétique, alors mesurer l'état d'un qubit est simplement mesurer l'énergie du système. Les postulats de la mécanique quantique dictent que si le système est dans une superposition de résultats de mesure possibles, alors l'acte de mesure doit changer l'état lui-même. Le système de superposition s'effondrera au stade de la mesure; la mesure détruit ainsi les informations portées par les amplitudes dans le qubit.
Des implications informatiques importantes surviennent lorsque nous considérons des systèmes de qubits multiples qui peuvent subir un enchevêtrement quantique. L'enchevêtrement est un phénomène dans lequel un groupe de qubits est corrélé, et toute opération sur l'un de ces qubits affectera l'état général de tous. Un exemple canonique d'intrication quantique est le paradoxe d'Einstein-Podolsky-Rosen, présenté en 1935 [cf. ici ]. Considérons un système de deux qubits, où, puisque chacun des qubits individuels peut prendre n'importe quelle superposition d'états {| 0⟩ et | 1⟩}, le système composite peut prendre n'importe quelle superposition d'états {| 00⟩, | 01⟩, | 10⟩, | 11 ⟩} (Et, par conséquent, le système de N-qubits peut prendre n'importe lequel deschaînes binaires, de {| 0 ... 0⟩ à | 1 ... 1⟩}. L'une des superpositions possibles du système sont les états dits de Bell, dont l'un a la forme suivante: Si nous prenons une mesure sur le premier qubit, nous ne pouvons observer que | 0⟩ ou | 1⟩, dont chacun aura une probabilité de 1/2. Cela n'apporte aucune modification pour le cas d'un seul qubit. Si le résultat pour le premier qubit était | 0⟩, le système s'effondrera vers le système | 01⟩, et par conséquent toute mesure sur le deuxième qubit donnera | 1⟩ avec une probabilité 1; de même, si la première mesure était | 1⟩, la mesure sur le deuxième qubit donnerait | 0⟩. Une opération (dans ce cas, une mesure avec le résultat "0") appliquée au premier qubit affecte les résultats qui peuvent être vus lorsque le deuxième qubit est ensuite mesuré.

L'existence de l'intrication est fondamentale pour l'informatique quantique utile. Il a été prouvé que tout algorithme quantique qui n'utilise pas l'intrication peut être appliqué à un ordinateur classique sans différence de vitesse significative [cf. ici et ici ]. Intuitivement, la raison est la quantité d'informations qu'un ordinateur quantique peut manipuler. Si le système N qubit n'est pas intriqué, alorsles amplitudes de son état peuvent être décrites par les amplitudes de chaque état d'un bit, c'est-à-dire 2N amplitudes. Cependant, si le système est intriqué, toutes les amplitudes seront indépendantes et le registre de qubit se formera-vecteur dimensionnel. La capacité des ordinateurs quantiques à manipuler de grandes quantités d'informations avec de multiples opérations est l'un des principaux avantages des algorithmes quantiques et sous-tend leur capacité à résoudre des problèmes de manière exponentielle plus rapidement que la technologie informatique classique.
1.1.2. Portes quantiques
Les informations stockées dans les qubits sont traitées à l'aide d'opérations spéciales appelées portes quantiques. Les portes quantiques sont des opérations physiques, telles qu'une impulsion laser dirigée vers un qubit ionique, ou un ensemble de miroirs et de séparateurs de faisceau à travers lesquels un qubit photon doit voyager. Cependant, les portes sont souvent considérées comme des opérations abstraites. Les postulats de la mécanique quantique imposent des conditions strictes sur la nature des portes quantiques dans les systèmes fermés, ce qui leur permet d'être représentées sous forme de matrices unitaires, qui sont des opérations linéaires qui préservent la normalisation du système quantique.
En particulier, une porte quantique appliquée à un registre intriqué de N qubits équivaut à multiplier la matrice × sur le vecteur d'entrée ... La capacité d'un ordinateur quantique à stocker et à effectuer des calculs de grandes quantités d'informations est de l'ordre de- en manipulant plusieurs éléments - d'ordre N - constitue la base de sa capacité à fournir un avantage potentiellement exponentiel par rapport aux ordinateurs classiques.
Essentiellement, les portes quantiques sont toute opération autorisée dans un système de qubit. Les postulats de la mécanique quantique imposent deux contraintes strictes sur la forme des portes quantiques. Les opérateurs quantiques sont linéaires. La linéarité est une condition mathématique qui a néanmoins des implications profondes pour la physique des systèmes quantiques et, par conséquent, comment ils peuvent être utilisés pour le calcul. Si l'opérateur linéaire est appliqué à la superposition d'états, alors le résultat est une superposition des états individuels affectés par l'opérateur. Dans un qubit, cela signifie: Les opérateurs linéaires peuvent être représentés sous forme de matrices, qui sont simplement des tableaux indiquant l'effet d'un opérateur linéaire sur chaque état de base. La figure 1 (c, d) montre une représentation matricielle de l'une des deux portes qubit et deux portes à un bit. Cependant, toutes les matrices ne représentent pas de véritables portes quantiques. Nous nous attendons à ce que les portes quantiques appliquées à une collection de qubits donnent un ensemble réel différent de qubits, en particulier normalisé (par exemple, dans l'équation (3), nous nous attendons à ce que
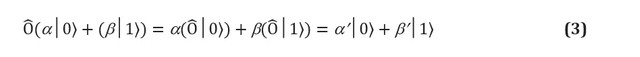
). Cette condition n'est satisfaite que si la matrice représentant les portes quantiques est unitaire, c'est-à-dire U † U = UU † = I, où U † est la matrice U dans laquelle les lignes et les colonnes ont été réorganisées, et chaque nombre complexe était conjugué (c'est-à-dire que chaque élément imaginaire acquiert un facteur négatif). Matrice unitaire arbitraire × est une porte quantique à N qubits entièrement valide.
Dans le calcul classique, il n'y a qu'une seule porte non triviale pour un bit: la porte NOT, qui convertit 0 en 1 et vice versa. En informatique quantique, il existe un nombre infini de matrices unitaires 2 × 2, et l'une d'entre elles est une porte quantique possible d'un qubit. L'un des premiers succès de l'informatique quantique a été la découverte que ce vaste éventail de possibilités pouvait être réalisé avec un ensemble de portes universelles affectant un et deux qubits [voir Réf. ici]. En d'autres termes, étant donné des portes quantiques arbitraires, il existe un circuit de portes à un et deux qubits qui peut le piloter avec une précision arbitraire. Malheureusement, cela ne signifie pas que l'approximation est efficace. La plupart des portes quantiques ne peuvent être approximées que par un nombre exponentiel de portes de notre ensemble universel. Même si ces portes peuvent être utilisées pour résoudre des problèmes utiles, leur mise en œuvre prendra un temps exponentiellement élevé et peut annuler tout avantage quantique. FIGURE 1 (a) Comparaison d'un bit classique avec un bit quantique ou "qubit". Alors qu'un bit classique ne peut prendre que l'un des deux états, 0 ou 1, un bit quantique peut prendre n'importe quel état de la forme

... Les qubits simples sont souvent représentés en utilisant la représentation de sphère de Bloch, où θ et ϕ sont compris comme des angles azimutaux et polaires dans une sphère de rayon unitaire. (b) Un schéma d'un qubit piège à ions, l'une des approches les plus courantes de l'informatique quantique expérimentale. Ion (souvent) est maintenu dans un vide poussé par des champs électromagnétiques et exposé à un champ magnétique puissant. Les niveaux hyperfins sont séparés selon l'effet Zeeman, et les deux niveaux sélectionnés sont sélectionnés comme états | 0⟩ et | 1⟩. Les portes quantiques sont mises en œuvre par des impulsions laser appropriées, impliquant souvent d'autres niveaux électroniques. Ce diagramme a été adapté de [voir. ici ]. (c) Schéma d'un circuit quantique qui implémente X ou le quantum de négation contrôlée (CNOT).
La représentation et le changement dans la sphère de Bloch sont affichés. (d) Circuit quantique pour générer l'état de Bellen utilisant une porte Hadamard et une porte CNOT (négation contrôlée). La ligne pointillée au milieu du contour indique l'état après l'application de la valve Hadamard.
1.2. Matériel quantique
Les algorithmes quantiques ne peuvent résoudre des problèmes intéressants que s'ils fonctionnent sur le bon matériel quantique. Il existe de nombreuses propositions concurrentes pour la création d'un processeur quantique basé sur des ions piégés [voir. ici ], circuits supraconducteurs [voir. ici ] et les dispositifs photoniques [voir. ici]. Cependant, ils sont tous confrontés à un problème commun: des erreurs de calcul qui peuvent littéralement ruiner le processus de calcul. L'une des pierres angulaires de l'informatique quantique est la découverte que ces erreurs peuvent être éliminées avec des codes de correction d'erreurs quantiques. Malheureusement, ces codes nécessitent également une très forte augmentation du nombre de qubits, des améliorations techniques importantes sont donc nécessaires pour atteindre la tolérance aux pannes.
De nombreuses sources d'erreur peuvent affecter un processeur quantique. Par exemple, la connexion d'un qubit avec son environnement peut conduire à l'effondrement du système dans l'un de ses états classiques - un processus connu sous le nom de décohérence.... De petites fluctuations peuvent transformer les portes quantiques, ce qui conduit finalement à des résultats différents de ceux attendus. Les portes les moins sujettes aux erreurs à ce jour ont été enregistrées dans un processeur d'ions piégés, avec une fréquence d'une erreur parportes à un qubit et avec un taux d'erreur de 0,1% pour les portes à deux qubit [ ici et ici ]. En comparaison, un travail récent de Google a rapporté une fidélité de 0,1% pour les portes à un qubit et de 0,3% pour les portes à deux qubits dans un processeur supraconducteur [voir Réf. ici ]. Étant donné que l'échec d'une passerelle peut ruiner le calcul, il est facile de voir que la propagation de l'erreur peut rendre le calcul inutile après une petite séquence d'éléments.
L'une des principales directions de l'informatique quantique est le développement de codes de correction d'erreur quantique. Dans les années 1990, plusieurs groupes de recherche ont prouvé que ces codes peuvent réaliser des calculs tolérants aux pannes, à condition que les taux d'erreur de porte soient inférieurs à un certain seuil, qui dépend du code [voir. ici , ici , ici et ici ]. L'une des approches les plus populaires, le code de surface, peut fonctionner avec des taux d'erreur approchant 1% [voir Réf. ici ].
Malheureusement, les codes de correction d'erreur quantique nécessitent un grand nombre de qubits physiques réels pour coder le qubit logique abstrait qui est utilisé pour le calcul, et cette surcharge augmente avec le taux d'erreur. Par exemple, un algorithme quantique pour factoriser les nombres premiers [voir. here ] pourrait tranquillement décomposer un nombre de 2000 bits en utilisant environ 4000 qubits et, à 16 GHz, ce processus prendrait environ une journée de travail. En supposant un taux d'erreur de 0,1%, le même algorithme, utilisant le code de surface pour corriger les erreurs environnementales, nécessiterait plusieurs millions de qubits et le même temps [voir Réf. ici]. Considérant que l'enregistrement actuel pour un processeur quantique programmable contrôlé est de 53 qubits [voir. ici ], il y a encore un long chemin à parcourir dans cette direction de recherche.
De nombreux groupes ont fait des efforts pour développer des algorithmes qui peuvent être exécutés sur des processeurs quantiques de bruit à moyenne échelle [voir Réf. ici ]. Par exemple, les algorithmes variationnels combinent un ordinateur classique avec un petit processeur quantique, effectuant une grande quantité de calculs quantiques courts qui peuvent être accomplis avant que le bruit ne devienne significatif.
Ces algorithmes utilisent souvent un circuit quantique paramétré, qui effectue une tâche particulièrement difficile, et utilisent un ordinateur classique pour optimiser les paramètres. La méthode de résolution est une région de réduction d'erreur dans laquelle, au lieu d'atteindre la tolérance aux pannes, une tentative a été faite pour minimiser les erreurs avec un effort minimal pour piloter des circuits de porte plus grands. Il existe un certain nombre d'approches qui incluent l'utilisation d'opérations supplémentaires pour ignorer les exécutions avec des erreurs [voir. ici ] ou manipulation du taux d'erreur pour extrapoler au résultat correct [cf. ici et ici]. Bien que les applications principales nécessitent de très gros ordinateurs quantiques tolérants aux pannes; les appareils disponibles au cours de la prochaine décennie devraient résoudre ces problèmes [voir ici ].
2. Méthodes statistiques et apprentissage automatique
En biologie computationnelle, où l'objectif est souvent de collecter des quantités massives de données, les méthodes statistiques et l'apprentissage automatique sont des techniques clés. Par exemple, en génomique, les modèles de Markov cachés (HMM) sont largement utilisés pour annoter des informations sur les gènes [voir. ici ]; au cours de la découverte de médicaments, un large éventail de modèles statistiques ont été développés pour évaluer les propriétés moléculaires ou pour prédire la liaison ligand-protéine [voir. ici ]; et en biologie structurale, des réseaux neuronaux profonds ont été utilisés à la fois pour prédire les connexions protéiques [voir. ici ] et structure secondaire [voir. ici ], et plus récemment aussi des structures de protéines tridimensionnelles [voir. ici ].
La formation et le développement de tels modèles demandent souvent beaucoup de calculs. L'un des principaux catalyseurs des progrès récents de l'apprentissage automatique a été la prise de conscience que les unités de traitement graphique (GPU) à usage général peuvent accélérer considérablement l'apprentissage. En fournissant des algorithmes exponentiellement plus rapides pour l'apprentissage automatique, les modèles de calcul quantique peuvent fournir un intérêt similaire pour la concentration d'application aux problèmes scientifiques.
Dans cette section, nous expliquerons comment l'informatique quantique peut accélérer de nombreuses méthodes d'apprentissage statistique.
2.1. Avantages et inconvénients de l'apprentissage automatique quantique
Nous examinons d'abord les avantages d'un ordinateur quantique pour l'apprentissage automatique. Hormis des exemples idéalisés, les ordinateurs quantiques ne peuvent pas apprendre plus d'informations qu'un ordinateur classique [cf. ici ]. Cependant, en principe, ils peuvent être beaucoup plus rapides et capables de traiter beaucoup plus de données que leurs homologues classiques. Par exemple, le génome humain contient 3 milliards de paires de bases, qui peuvent être stockées dans 1,2 ×bits classiques - environ 1,5 gigaoctets. Un registre de N qubits comprendamplitudes, dont chacune peut représenter un bit classique en mettant la k-ième amplitude à 0 ou 1 avec un facteur de normalisation approprié. Par conséquent, le génome humain peut être stocké dans environ 34 qubits. Bien que ces informations ne puissent pas être extraites d'un ordinateur quantique, jusqu'à ce qu'un certain état soit préparé, certains algorithmes d'apprentissage automatique peuvent être exécutés sur celui-ci. Plus important encore, doubler la taille du registre à 68 qubits laisse suffisamment de place pour stocker le génome complet de chaque personne vivante dans le monde. La présentation et l'analyse de ces énormes quantités de données seraient tout à fait compatibles avec les capacités d'un petit ordinateur quantique tolérant aux pannes.
Les opérations de traitement de ces informations peuvent également être exponentiellement plus rapides. Par exemple, plusieurs algorithmes d'apprentissage automatique sont limités à l'inversion à long terme de la matrice de covariance avec une pénalitésur les dimensions de la matrice. Cependant, l'algorithme proposé par Harrow, Hassidim et Lloyd [cf. here ], vous permet d'inverser la matrice ensous certaines conditions. L'idée clé est que, contrairement aux GPU, qui accélèrent les calculs grâce à un parallélisme massif, les algorithmes quantiques ont l'avantage de la complexité des algorithmes de calcul directement utilisés. Dans certains cas, en particulier avec l'accélération exponentielle actuelle, les ordinateurs quantiques de taille moyenne peuvent résoudre des problèmes d'apprentissage disponibles uniquement pour les plus grands supercalculateurs classiques disponibles aujourd'hui.
L'amélioration du stockage et du traitement des données présente des avantages secondaires. L'une des forces des réseaux de neurones est leur capacité à trouver des représentations concises des données [voir. ici]. Étant donné que les informations quantiques sont plus générales que les informations classiques (après tout, les états d'un bit classique sont subdivisés en états propres | 0 | et | 1⟩, ou un qubit), il est tout à fait possible que les modèles d'apprentissage automatique quantique puissent mieux assimiler les informations que les modèles classiques ... D'autre part, les algorithmes quantiques à complexité temporelle logarithmique améliorent également la confidentialité des données [cf. ici ]. Puisque la formation du modèle nécessite, et nécessite une reconstruction de la matrice, pour un ensemble de données suffisamment grand, il est impossible de récupérer une partie significative de l'information, bien qu'un entraînement efficace du modèle soit toujours possible. Dans le cadre de la recherche biomédicale, cela peut faciliter l'échange de données tout en garantissant la confidentialité.
Malheureusement, bien que les algorithmes d'apprentissage automatique quantique sur papier puissent largement surpasser leurs homologues classiques, des difficultés pratiques subsistent. Les algorithmes quantiques sont souvent des sous-programmes qui transforment l'entrée en sortie. Des problèmes surviennent précisément à ces deux étapes: comment préparer une entrée adéquate et comment extraire des informations de la sortie [voir. ici ]. Supposons, par exemple, que nous utilisons l'algorithme HHL [voir. ici ] pour résoudre un système linéaire de la forme... À la fin du sous-programme, l'algorithme sortira le registre qubit dans l'état suivant: Ici
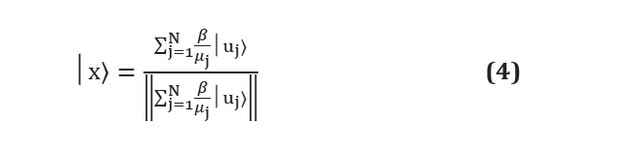
et Les vecteurs propres et les valeurs propres de A, et - j-ième coefficient est exprimé en termes de vecteurs propres de A, et le dénominateur est simplement une constante de normalisation. On voit que cela correspond aux coefficients, qui sont stockées dans les amplitudes de divers états comme et ne sont pas directement accessibles. La mesure du registre qubit conduira à son effondrement dans l'un des états du vecteur propre, et à ré-estimer les amplitudes de chacun mesures requises , ce qui en premier lieu l'emporte sur tout avantage de l'algorithme quantique.
HHL et de nombreux autres algorithmes ne sont utiles que pour calculer la propriété globale d'une solution, telle que la valeur attendue. En d'autres termes, HHL ne peut pas fournir une solution à un système d'équations ou inverser une matrice en temps logarithmique, si l'on ne s'intéresse pas uniquement aux propriétés globales de la solution, qui peuvent être obtenues à l'aide de plusieurs mesures physiquement observables. Cela limite l'utilisation de certains sous-programmes, mais il y a eu de nombreuses suggestions pour contourner ce problème.
La saisie d'informations dans un ordinateur quantique est un problème beaucoup plus important. La plupart des algorithmes d'apprentissage automatique quantique supposent que l'ordinateur quantique a accès à l'ensemble de données sous la forme d'un état de superposition; par exemple, il y a un registre qubit qui est dans un état de la forme: Ici - | bin (j) est un état qui agit comme un index, et

Est l'amplitude correspondante. Cela peut être utilisé, par exemple, pour stocker les éléments d'un vecteur ou d'une matrice. En principe, il existe un circuit quantique qui peut préparer cet état en agissant, par exemple, dans l'état | 0 ... 0⟩. Cependant, sa mise en œuvre peut être très difficile, car nous prévoyons que l'approximation d'un état quantique aléatoire sera exponentiellement difficile et détruira tout avantage quantique éventuel.
La plupart des algorithmes quantiques supposent un accès à la mémoire quantique à accès aléatoire (QRAM) [voir. ici ], qui est un dispositif boîte noire capable de construire cette superposition. Bien que certains dessins aient été proposés [voir. ici et ici], pour autant que nous le sachions, il n'y a pas encore de dispositif fonctionnel. De plus, même si un tel dispositif était disponible, il n'y a aucune garantie qu'il ne créera pas de goulots d'étranglement qui l'emporteront sur les avantages de l'algorithme quantique. Par exemple, une récente proposition basée sur un schéma pour QRAM [cf. here ] montre le coût linéaire inévitable du nombre d'états qui l'emporte sur tout algorithme de temps logarithmique. Enfin, même si QRAM n'introduit aucun coût supplémentaire, le prétraitement classique devra encore être effectué - pour l'exemple du génome, l'accès à 12 exaoctets de stockage classique serait nécessaire.
Enfin, nous devons souligner que les algorithmes d'apprentissage automatique quantique ne sont pas exempts de l'un des problèmes les plus courants dans les applications pratiques: le manque de données pertinentes. La disponibilité de grandes quantités de données est essentielle au succès de nombreuses applications pratiques de l'IA en science moléculaire, telles que le développement moléculaire de novo [voir Réf. ici ]. Cependant, la puissance des algorithmes quantiques peut être utile en tant que développements scientifiques et technologiques tels que l'émergence de laboratoires autogérés [voir Réf. here ] fournissent de plus en plus de données.
L'apprentissage automatique quantique a le potentiel de transformer la façon dont nous traitons et analysons les données biologiques. Cependant, les problèmes pratiques actuels de mise en œuvre des technologies quantiques sont encore importants.
2.2. Algorithmes d'apprentissage automatique quantique
2.2.1. Apprendre sans enseignant
L'apprentissage non supervisé comprend plusieurs techniques pour extraire des informations d'ensembles de données non étiquetés. En biologie, où le séquençage de nouvelle génération et une grande collaboration internationale ont stimulé la collecte de données, ces méthodes ont trouvé une large utilisation, par exemple, pour identifier des liens entre les familles de biomolécules [voir. ici ] ou des génomes annotés [voir. ici ].
Un des algorithmes d'apprentissage non supervisé les plus populaires est l'analyse en composantes principales (ACP), qui tente de réduire la dimensionnalité des données en trouvant des combinaisons linéaires de caractéristiques qui maximisent la variance [cf. ici]. Cette méthode est largement utilisée dans toutes sortes d'ensembles de données à haute dimension, y compris les données de microréseau à ARN et de spectrométrie de masse [voir. ici ]. Un algorithme quantique pour l'ACP a été proposé par un groupe de chercheurs [voir. ici ]. Essentiellement, cet algorithme construit une matrice de covariance de données dans un ordinateur quantique et utilise un sous-programme connu sous le nom d'estimation de phase quantique pour calculer les vecteurs propres en temps logarithmique. Les données de sortie de l'algorithme sont un état de superposition de la forme: Ici

Est le j-ème composant principal, et - la valeur propre correspondante. Puisque l'ACP s'intéresse aux grandes valeurs propres, qui sont les principales composantes de la variance, la mesure de l'état final donnera une composante principale appropriée avec une probabilité élevée. La répétition de l'algorithme plusieurs fois fournira un ensemble de composants de base. Cette procédure est capable de réduire la dimension de la grande quantité d'informations qui peuvent être stockées dans un ordinateur quantique.
Un algorithme quantique a également été proposé pour une méthode particulière d'analyse de données topologiques, à savoir pour une homologie stable [voir. ici ]. L'analyse des données topologiques tente d'extraire des informations en utilisant des propriétés topologiques dans la géométrie des ensembles de données; il a été utilisé, par exemple, dans l'étude de l'agrégation des données [voir.ici ] et analyse de réseau [voir. ici ]. Malheureusement, les meilleurs algorithmes classiques ont une dépendance exponentielle dans la dimension du problème, ce qui limite son application. Algorithme Lloyd et al. utilise également une routine d'estimation de phase quantique pour accélérer de manière exponentielle la diagonalisation de la matrice, atteignant ainsi la complexité... La présence d'un algorithme efficace pour mener une analyse topologique peut stimuler son application pour l'analyse de problèmes en sciences biologiques.
2.2.2. Enseignement supervisé
L'apprentissage supervisé fait référence à un ensemble de méthodes qui peuvent être utilisées pour faire des prédictions basées sur des données étiquetées. L'objectif est de construire un modèle capable de classer ou de prédire les propriétés d'exemples invisibles. L'apprentissage supervisé est largement utilisé en biologie pour résoudre des problèmes aussi divers que la prédiction de l'affinité de liaison d'un ligand pour une protéine [voir. ici ] et le diagnostic des maladies à l'aide d'un ordinateur [voir. ici ]. Examinons trois approches d'apprentissage supervisé.
Machine à vecteur de soutien(English support vector machine - SVM) est un algorithme d'apprentissage automatique qui trouve l'hyperplan optimal séparant les classes de données. SVM a été largement utilisé dans l'industrie pharmaceutique pour classer les données de petites molécules [cf. ici ]. Selon le noyau, la formation SVM prend généralement avant ... Rebentrost [voir. here ] a présenté un algorithme quantique qui peut entraîner un SVM avec un noyau polynomial en, et plus tard, il a été étendu au cœur de la fonction de base radiale (RBF) [voir. ici ]. Malheureusement, il n'est pas clair comment implémenter les opérations non linéaires qui sont largement utilisées dans SVM, étant donné que les opérations quantiques sont limitées à être linéaires. D'un autre côté, un ordinateur quantique autorise d'autres types de noyaux qui ne peuvent pas être implémentés dans un ordinateur classique [voir. ici ].
La régression de processus gaussien (GP) est une technique couramment utilisée pour construire des modèles de substitution, par exemple dans l'optimisation bayésienne [voir. ici ]. Les médecins généralistes sont également largement utilisés pour créer des modèles de relations quantitatives structure-activité (QSAR) des propriétés des médicaments.here ], et récemment aussi pour la modélisation de la dynamique moléculaire [voir. ici ]. L'un des inconvénients de la régression GP est la valeur élevéeinversion de la matrice de covariance. Zhao et ses collègues [voir. here ] a suggéré d'utiliser l'algorithme HHL pour les systèmes linéaires pour inverser cette matrice, obtenant une accélération exponentielle (tant que la matrice est clairsemée et bien conditionnée) - une propriété qui est souvent obtenue par les matrices de covariance. Plus important encore, cet algorithme a été étendu pour calculer le logarithme de la vraisemblance limite [cf. here ], qui est une étape importante pour l'optimisation des hyperparamètres.
L'une des méthodes les plus courantes en biologie computationnelle est le modèle de Markov caché (HMM), qui est largement utilisé dans l'annotation computationnelle de gènes et l'alignement de séquences [cf. ici]. Cette méthode contient un certain nombre d'états cachés, chacun étant associé à une chaîne de Markov; les transitions entre les états cachés entraînent des changements dans la distribution sous-jacente. Fondamentalement, HMM ne peut pas être directement implémenté dans un ordinateur quantique: l'échantillonnage nécessite une sorte de mesure qui perturbera le système. Cependant, il existe une formulation en termes de systèmes quantiques ouverts, c'est-à-dire un système quantique en contact avec l'environnement, qui permet un système de Markov [voir. ici ]. Bien qu'aucune amélioration n'ait été proposée à l'algorithme classique de Baum-Welch pour la formation des HMMs, les HMM quantiques se sont révélées plus expressives: elles peuvent reproduire une distribution avec moins d'états cachés [cf. ici]. Cela pourrait conduire à une application plus large de la méthode en biologie computationnelle.
2.2.3. Réseaux de neurones et apprentissage profond
Les développements récents de l'apprentissage automatique ont été stimulés par la découverte que de multiples couches de réseaux de neurones artificiels peuvent détecter des structures complexes dans les données brutes [voir p. ici ]. L'apprentissage en profondeur a commencé à imprégner toutes les disciplines scientifiques et, en biologie computationnelle, ses progrès incluent la prédiction précise des liaisons protéiques. ici ], un diagnostic amélioré de certaines maladies [voir. ici ], conception moléculaire [cf. ici ] et la modélisation [voir. ici et ici ].
Compte tenu des progrès significatifs dans l'étude des réseaux de neurones, des travaux importants ont été réalisés pour développer des analogues quantiques qui peuvent conduire à de nouvelles avancées technologiques.
Le nom de réseau neuronal artificiel fait souvent référence au perceptron multicouche d'un réseau neuronal, où chaque neurone prend une combinaison linéaire pondérée de ses entrées et renvoie le résultat via une fonction d'activation non linéaire. Le principal défi du développement d'un analogue quantique est de savoir comment implémenter une fonction d'activation non linéaire à l'aide de portes quantiques linéaires. Il y a eu beaucoup de propositions ces derniers temps, et certaines idées incluent des mesures [voir p. ici , ici et ici ], portes quantiques dissipatives [ ici], le calcul quantique avec une variable continue [ ici ] et l'introduction de qubits supplémentaires pour construire des portes linéaires qui simulent la non-linéarité [voir. ici ]. Ces approches visent à mettre en œuvre un réseau de neurones quantiques qui devrait être plus expressif qu'un réseau de neurones classique en raison de la plus grande puissance des informations quantiques. Les avantages ou les inconvénients de la mise à l'échelle de la formation d'un perceptron multicouche dans un ordinateur quantique ne sont pas clairs, bien que l'accent soit mis sur la possible expressivité améliorée de ces modèles.
Un énorme effort récent s'est concentré sur les machines Boltzmann, des réseaux de neurones récurrents capables d'agir comme des modèles génératifs. Une fois formés, ils peuvent générer de nouveaux modèles similaires à l'ensemble d'apprentissage.
Les modèles génératifs ont des applications importantes, par exemple dans la conception moléculaire de novo [cf. ici et ici ]. Bien que les machines de Boltzmann soient très puissantes, il est nécessaire de résoudre le problème complexe de l'échantillonnage à partir de la distribution de Boltzmann afin de calculer des gradients et de mener des formations, ce qui limite leur application pratique. Des algorithmes quantiques ont été proposés en utilisant la machine D-Wave [voir. ici , ici et ici ] ou un algorithme de circuit [voir.ici ]; cet échantillon de la distribution de Boltzmann est quadratiquement plus rapide que ce qui est possible dans la version classique [voir. ici ].
Récemment, une heuristique pour un entraînement efficace des machines quantiques de Boltzmann a été proposée, basée sur la thermalisation du système [voir. ici ]. De plus, dans certains travaux, des implémentations quantiques de réseaux antagonistes génératifs (GAN) ont été proposées [voir. ici , ici et ici ]. Ces développements impliquent d'améliorer les modèles génératifs à mesure que le matériel informatique quantique se développe.
3. Simulation efficace des systèmes quantiques
Selon les modèles, la chimie est régulée par transfert d'électrons. Les réactions chimiques, ainsi que les interactions entre les entités chimiques, sont également contrôlées par la distribution des électrons et le paysage d'énergie libre qu'ils forment. Des problèmes tels que la prédiction de la liaison d'un ligand à une protéine ou la compréhension de la voie catalytique d'une enzyme se résument à la compréhension de l'environnement électronique. Malheureusement, la modélisation de ces processus est extrêmement difficile. L'algorithme le plus efficace pour calculer l'énergie d'un système d'électrons, l'interaction de configuration complète (FCI), qui évolue de façon exponentielle à mesure que le nombre d'électrons augmente, et même les molécules avec plusieurs atomes de carbone sont à peine disponibles pour la recherche informatique [voir. ici]. Bien qu'il existe de nombreuses méthodes approximatives, décrites en profondeur et en détail dans les publications sur la théorie fonctionnelle de la densité [voir. ici et ici ], ils peuvent être imprécis et même brusquement échouer dans de nombreuses situations d'intérêt, comme la simulation d'un état de réponse transitoire [cf. ici ]. Un algorithme précis et efficace pour étudier la structure électronique fournirait une meilleure compréhension des processus biologiques et ouvrirait également des opportunités pour le développement d'interactions biologiques de prochaine génération.
Les ordinateurs quantiques ont été proposés à l'origine comme une méthode de modélisation plus efficace des systèmes quantiques. En 1996, Seth Lloyd a démontré que cela est possible pour certains types de systèmes quantiques [ ici], et une décennie plus tard, Alan Aspuru-Guzik et ses collègues ont montré que les systèmes chimiques sont un tel cas [ ici ]. Au cours des deux dernières décennies, d'importantes recherches ont été menées pour affiner les méthodes de modélisation des systèmes chimiques capables de calculer les propriétés d'intérêt pour la recherche.
3.1. Avantages et inconvénients de la simulation quantique
En principe, un ordinateur quantique est capable de résoudre efficacement un problème de structure électronique entièrement corrélé (équations FCI), qui sera la première étape pour estimer avec précision les énergies de liaison, ainsi que pour simuler la dynamique des systèmes chimiques. La chimie computationnelle classique s'est concentrée presque exclusivement sur des méthodes approximatives, utiles, par exemple, pour estimer les quantités thermochimiques de petites molécules [ ici], mais cela peut ne pas être suffisant pour les processus associés à la rupture ou à la formation de liaisons. En revanche, les processeurs quantiques peuvent potentiellement résoudre un problème électronique en diagonalisant directement la matrice FCI, donnant un résultat précis dans un certain ensemble de bases et résolvant ainsi de nombreux problèmes résultant de descriptions incorrectes de la physique des processus moléculaires (par exemple, polarisation des ligands) ... De plus, contrairement aux approches classiques, elles ne nécessitent pas nécessairement un processus itératif, bien que l'hypothèse initiale soit toujours importante.
Bien que les ordinateurs quantiques ne soient pas aussi étudiés en profondeur, ils surmontent également les approximations limites qui étaient nécessaires dans le calcul classique. Par exemple, la formulation de la simulation quantique dans l'espace réel prend automatiquement en compte la fonction d'onde nucléaire en l'absence d'approximation de Born-Oppenheimer [ ici ]. Cela permet d'étudier les effets non adiabatiques de certains systèmes qui sont connus pour être importants pour la mutation de l'ADN [voir. ici ] et le mécanisme d'action de nombreuses enzymes [ ici ]. Des applications de l'informatique quantique pour la modélisation de systèmes relativistes ont également été proposées [voir. here ], qui sont utiles pour étudier les métaux de transition qui apparaissent dans les centres actifs de nombreuses enzymes.
Dans un article de Reicher et de ses collègues [voir ici ] le concept d'échelle de temps pour le calcul des structures électroniques dans un ordinateur quantique est révélé. Les auteurs ont considéré le cofacteur FeMo de l'enzyme nitrogénase, dont le mécanisme de fixation de l'azote n'a pas encore été étudié et est trop complexe pour être étudié à l'aide d'approches informatiques modernes. Le calcul de la FCI de base minimale pour FeMoCo prendra plusieurs mois et environ 200 millions de qubits de la classe la plus élevée disponible aujourd'hui. Cependant, ces estimations doivent changer avec le développement rapide de la technologie. Au cours des 3 années écoulées depuis la publication, les progrès algorithmiques ont déjà réduit les délais de plusieurs ordres de grandeur [voir. ici]. En plus des méthodes plus puissantes de structure électronique, des versions rapides de méthodes modernes approximatives qui ont été étudiées récemment [cf. ici et ici ] peuvent considérablement accélérer le prototypage, ce qui pourrait être utile, par exemple, lors de l'étude des coordonnées de réactions de réactions enzymatiques, dont le domaine est un problème pour l'enzymologie computationnelle [ ici ]. De plus, avec une meilleure compréhension des interactions intermoléculaires catalysées par l'accès à un calcul entièrement corrélé ou l'accès à une bande passante plus rapide qui améliore le paramétrage, la modélisation quantique peut considérablement améliorer les techniques de modélisation non quantiques telles que les champs de force.
Un dernier point à surveiller est que, contrairement à d'autres domaines de recherche d'algorithmes, tels que l'apprentissage avec des machines quantiques, il existe un certain nombre d'algorithmes de simulation quantique à court terme qui peuvent être exécutés sur du matériel préexistant peu exigeant. De nombreux groupes expérimentaux à travers le monde ont rapporté des démonstrations réussies de ces algorithmes [ ici , ici , ici et ici ].
Malheureusement, la modélisation des systèmes quantiques présente également certains inconvénients. Comme discuté ci-dessus, il est très difficile d'extraire des informations d'un ordinateur quantique. Reconstruire la fonction d'onde entière est plus difficile que de la calculer de manière classique. C'est un inconvénient important pour les problèmes chimiques, où les arguments basés sur la structure électronique sont la principale source de compréhension. Cependant, par rapport à l'apprentissage automatique, les avantages l'emportent largement sur les inconvénients, et la simulation quantique devrait être l'une des premières applications utiles de l'informatique quantique pratique [voir Réf. ici ].
3.2. Calcul quantique tolérant aux pannes
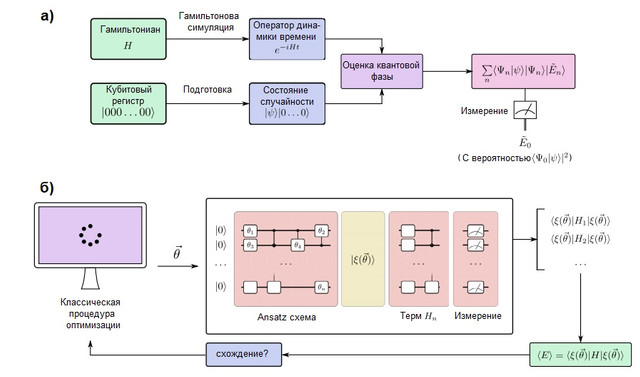
FIGURE 2. (a) Un algorithme de simulation quantique dans un ordinateur quantique tolérant aux pannes. Les qubits sont divisés en deux registres: l'un est préparé à l'état, qui ressemble à la fonction d'onde cible, tandis que l'autre reste dans l'état ... L'algorithme d'estimation de phase quantique (QPE) est utilisé pour trouver les valeurs propres de l'opérateur d'évolution temporelle, qui est préparé en utilisant les méthodes de modélisation hamiltonienne. Après QPE, la mesure d'un ordinateur quantique donne l'énergie de l'état fondamental avec probabilitéil est donc important de préparer l'état de la supposition avec chevauchement non nul avec la fonction d'onde vraie. (b) Un algorithme de simulation quantique variationnelle dans un ordinateur quantique à court terme. Cet algorithme combine un processeur quantique avec des routines d'optimisation classiques pour effectuer plusieurs courtes séries suffisamment rapides pour éviter les erreurs. Un ordinateur quantique prépare un état de conjectureavec une chaîne ansatz quantique dépendant de plusieurs paramètres... Les termes individuels de l'hamiltonien sont mesurés un par un (ou en groupes de navettage en utilisant des stratégies plus avancées), donnant une estimation de l'énergie attendue pour un vecteur particulier de paramètres. Ensuite, les paramètres sont optimisés par la procédure d'optimisation classique jusqu'à convergence. L'approche variationnelle a été étendue à de nombreux problèmes algorithmiques en plus de la simulation quantique.
Les ordinateurs quantiques capables de simuler de grands systèmes chimiques doivent être tolérants aux pannes afin d'exécuter des algorithmes arbitrairement profonds sans erreur. Un tel ordinateur quantique est capable de simuler un système chimique en cartographiant le comportement de ses électrons avec le comportement de ses qubits et portes quantiques. Le processus de modélisation quantique est conceptuellement très simple et est illustré à la figure 2 (a). Nous allons préparer un registre de qubits pouvant stocker la fonction d'onde et implémenter l'évolution unitaire de l'hamiltonienen utilisant les méthodes de modélisation hamiltonienne, qui sont discutées ci-dessous. Avec ces éléments, un sous-programme quantique connu sous le nom d'estimation de phase quantique est capable de trouver les vecteurs propres et les valeurs propres du système. A savoir, si le registre qubit est initialement dans l'état | 0⟩, l'état final sera: En d'autres termes, l'état final est une superposition de valeurs propres

et vecteurs propres systèmes. L'état fondamental est ensuite mesuré avec probabilité... Pour maximiser cette probabilité, une ligne de base est établie comme un état facile à préparer mais aussi motivé physiquement qui devrait être similaire à l'état fondamental exact. Un exemple typique est l'état de Hartree-Fock, bien que d'autres idées aient été explorées pour des systèmes fortement corrélés [voir Réf. ici ].
Il existe deux façons courantes de représenter les électrons dans une molécule: les méthodes basées sur la grille et les méthodes orbitales ou de base (voir McArdle et ses collègues pour une ventilation complète [ ici ]). Dans les méthodes par ensembles de base, la fonction d'onde électronique est représentée comme une somme des déterminants de Slater des orbitales d'électrons, qui peuvent être directement comparées au registre qubit [ ici etici ]. Cela nécessite le choix d'une base et le calcul préalable des intégrales électroniques. D'autre part, dans les méthodes de grille, le problème est formulé comme une solution à une équation différentielle ordinaire dans une grille. L'avantage de la modélisation basée sur la grille est qu'aucune approximation de Bourne-Oppenheimer ou ensemble de base n'est requis. Cependant, ils ne sont pas naturellement antisymétriques, ce qui est requis par le principe de Pauli de la mécanique quantique, il est donc nécessaire de fournir une antisymétrie en utilisant la procédure de tri [ ici ]. Les méthodes basées sur la grille ont été discutées dans le cadre des simulations de dynamique chimique [cf. ici ] et calcul de la constante de vitesse thermique [voir. ici]. Malgré les différences, le flux de travail de modélisation quantique est identique, comme le montre la figure 2.
Il existe également plusieurs façons de construire l'opérateur... Nous présenterons la technique la plus simple, la trottérisation, également appelée formulation de produit [voir p. ici ]; pour un aperçu complet, voir [ ici et ici ]. La trottérisation est basée sur la prémisse que l'hamiltonien moléculaire peut être divisé comme la somme des termes décrivant les interactions à un et deux électrons. Si tel est le cas, l'opérateurpeut être implémenté en termes d'opérateurs correspondants pour chaque terme dans l'hamiltonien en utilisant la formule Trotter - Suzuki [ ici ]: Par exemple, dans la deuxième quantification, chaque terme de cette expression aura la forme ou , où sont les opérateurs d'annihilation et de création, respectivement. Des constructions de schémas explicites et détaillés représentant ces termes ont été données par Whitfield et ses collègues [cf. ici ]. Après avoir calculé les membres
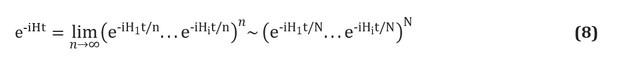

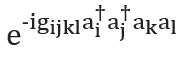
 et appelés intégrales électroniques, la quantitécomplètement déterminé. Vous pouvez également utiliser des formules Trotter - Suzuki d'ordre supérieur pour réduire l'erreur. Il existe de nombreuses autres techniques de modélisation hamiltoniennes. Des exemples de techniques puissantes et sophistiquées sont la cubitisation [ ici ] et le traitement du signal quantique [voir Réf. here ], qui ont une mise à l'échelle asymptotique optimale prouvée, bien qu'il ne soit pas clair si cela conduira à de meilleures applications pratiques.
et appelés intégrales électroniques, la quantitécomplètement déterminé. Vous pouvez également utiliser des formules Trotter - Suzuki d'ordre supérieur pour réduire l'erreur. Il existe de nombreuses autres techniques de modélisation hamiltoniennes. Des exemples de techniques puissantes et sophistiquées sont la cubitisation [ ici ] et le traitement du signal quantique [voir Réf. here ], qui ont une mise à l'échelle asymptotique optimale prouvée, bien qu'il ne soit pas clair si cela conduira à de meilleures applications pratiques.
4. Problèmes d'optimisation
De nombreux problèmes en biologie computationnelle et dans d'autres disciplines peuvent être formulés comme la recherche du minimum ou du maximum global d'une fonction multidimensionnelle complexe. Par exemple, on pense que la structure native d'une protéine est le minimum global de son hypersurface d'énergie libre [voir. ici ]. Dans un autre domaine, identifier des groupes dans un réseau de protéines ou d'objets biologiques en interaction équivaut à trouver un sous-ensemble optimal de nœuds [voir. ici]. Malheureusement, à l'exception de quelques systèmes simples, les problèmes d'optimisation sont souvent très complexes. Bien qu'il existe des heuristiques pour trouver des solutions approximatives, elles ne donnent généralement que des minima locaux et, dans de nombreux cas, même l'heuristique est indécidable. La capacité des ordinateurs quantiques à accélérer les solutions à de tels problèmes d'optimisation ou à trouver de meilleures solutions a été étudiée en détail.
Le sujet de l'optimisation dans un ordinateur quantique est complexe car il n'est souvent pas évident qu'un ordinateur quantique puisse fournir un type d'accélération quelconque. Dans cette section, nous donnerons un aperçu de certaines des idées d'optimisation quantique. Cependant, les garanties d'amélioration ne sont pas aussi claires par rapport à, par exemple, la simulation quantique, qui devrait être bénéfique à long terme.
4.1. Optimisation dans un processeur quantique
L'optimisation adiabatique quantique est l'une des approches d'optimisation les plus populaires en raison de la présence de machines D-Wave [voir. ici ] qui implémentent initialement cette approche. Le calcul quantique adiabatique [ ici ] est basé sur le théorème adiabatique de la mécanique quantique [cf. ici]. Selon ce théorème, si un système est préparé dans l'état fondamental de l'hamiltonien, et que cet hamiltonien change assez lentement, le système restera toujours dans son état fondamental instantané. Cela peut être utilisé pour effectuer des calculs en codant un problème (comme une fonction de notation que nous espérons minimiser) comme un hamiltonien, et en évoluant progressivement vers cet hamiltonien à partir d'un système original qui peut être préparé de manière triviale dans son état fondamental. En général, l'évolution adiabatique s'exprime comme suit: Ici

et - fonctions telles que et pendant un certain temps T. Par exemple, on pourrait considérer un programme de recuit linéaire avec et ... De nombreux articles ont été consacrés à la discussion du temps d'exécution de l'algorithme adiabatique, mais l'heuristique générale est que le temps d'exécution est au maximum proportionnel au carré inverse de l'écart spectral minimum (la plus petite différence d'énergie entre le sol et les premiers états excités) au cours de l'évolution adiabatique... On pense que l'informatique quantique adiabatique (et l'informatique quantique en général) n'est pas capable de résoudre efficacement la classe des problèmes NP-complets, ou du moins aucune de ces méthodes n'a résisté à des tests rigoureux [voir Réf. ici ].
En principe, le calcul quantique adiabatique équivaut au calcul quantique universel [cf. ici ]. Cette universalité n'a lieu que si l'évolution permet la non-stochasticité, ce qui signifie que l'hamiltonien a des éléments hors diagonale non négatifs à un moment donné de l'évolution. L'implémentation expérimentale la plus populaire de l'informatique quantique adiabatique, commercialisée par D-Wave Systems Inc., utilise des hamiltoniens stochastiques et n'est donc pas universelle. Il y a une certaine inquiétude dans la littérature professionnelle que cette variété de calcul quantique pourrait être simulée classiquement [ ici ], ce qui signifie qu'une accélération exponentielle pourrait ne pas être possible. Malgré ces préoccupations, cette technique a été largement utilisée comme technique d'optimisation métaheuristique et s'est récemment avérée supérieure au recuit simulé [voir Réf. ici ].
L'optimisation quantique a été étudiée en dehors du modèle adiabatique. L'algorithme d'optimisation approchée quantique (QAOA) [cf. ici , ici et ici] Est un algorithme d'optimisation variationnelle dans un ordinateur quantique qui a suscité un intérêt considérable dans la littérature. Il y a eu plusieurs implémentations expérimentales de QAOA dans les processeurs quantiques, par exemple [voir. ici ] Figure 3. FIGURE 3. (a) Simulation d'un ordinateur quantique adiabatique mettant en œuvre le problème simplifié de repliement des protéines décrit [ ici ]. La couleur code la probabilité logarithmique décimale d'une chaîne binaire particulière. A la fin du calcul, les deux solutions les plus énergétiques ont une probabilité de mesure proche de 0,5. L'évolution n'est jamais complètement adiabatique en un temps fini, et d'autres chaînes binaires ont des probabilités de mesure résiduelles. (b)

Description du processus adiabatique de l'informatique quantique. Le potentiel de conduite des qubits change lentement, ce qui les fait tourner. Notez que la représentation de la sphère de Bloch est incomplète car elle n'affiche pas les corrélations entre les différents qubits qui sont nécessaires pour l'avantage quantique. En fin d'évolution, le système qubit est dans un état classique (ou une superposition d'états classiques), représentant la solution avec l'énergie la plus faible. (c) Niveaux d'énergie au cours de l'évolution quantique adiabatique. Le temps nécessaire pour assurer une évolution quasi-adiabatique est déterminé par la différence d'énergie minimale entre les niveaux, qui est indiquée par la ligne en pointillés
4.2. Prédiction de la structure des protéines
La prédiction de la structure des protéines sans matrice reste un problème majeur non résolu en biologie computationnelle. La solution à ce problème trouvera une large application dans l'ingénierie moléculaire et la conception de médicaments. Selon l'hypothèse du repliement des protéines, la structure native d'une protéine est considérée comme un minimum global de son énergie libre [voir. ici ], bien qu'il existe de nombreux contre-exemples. Étant donné le vaste espace conformationnel disponible même pour les petits peptides, des simulations classiques exhaustives sont insolubles. Cependant, beaucoup se demandent si l'informatique quantique peut aider à résoudre ce problème.
La littérature informatique quantique se concentre sur le modèle de réseau de protéines, où un peptide est modélisé comme une structure de réseau autopropulsée, bien que plusieurs autres modèles aient également récemment commencé à être appliqués dans la pratique informatique [cf. ici ]. Chaque site de réseau correspond à un résidu, et les interactions entre sites voisins dans l'espace contribuent à la fonction énergétique. Il existe plusieurs schémas de contact énergétique, mais seuls deux ont été utilisés dans des applications quantiques: le modèle hydrophobe-polaire [voir. here ], qui ne considère que deux classes d'acides aminés, et le modèle de Miyazawa-Jernigan [cf. ici], contenant les interactions pour chaque paire de résidus. Bien que ces modèles soient une simplification marquée, ils ont fourni un aperçu substantiel du repliement des protéines [voir Réf. here ] et ont été proposés comme un outil brut pour étudier l'espace conformationnel avant un raffinement plus détaillé [voir. ici et ici ].
Presque tous les travaux se sont concentrés sur l'informatique quantique adiabatique, car même les peptides modèles nécessitent un grand nombre de qubits, et les machines quantiques D-Wave sont les plus grands dispositifs quantiques disponibles aujourd'hui.
Cependant, dans un article récemment publié par Fingerhat et ses collègues [voir ici] une tentative a été faite pour décrire l'utilisation de l'algorithme QAOA. Les deux méthodes ont des caractéristiques similaires si le problème de réseau de protéines est codé comme l'opérateur de Hamilton. Cette méthode a d'abord été considérée par Perdomo [voir. here ], qui suggérait d'utiliser un registre qubitpour coder les coordonnées cartésiennes de N acides aminés sur un réseau cubique de dimension D. à côtés N. La fonction énergétique est exprimée dans un hamiltonien contenant des termes pour récompenser les contacts avec les protéines: préserver la structure primaire et éviter les correspondances d'acides aminés. Peu de temps après cet article marquant, un autre article est apparu sur la construction de modèles plus efficaces en bits pour un réseau bidimensionnel [voir. ici ].
Ces encodages ont été testés sur du matériel réel en 2012 lorsque Perdomo et ses collègues [voir. ici] a calculé la conformation d'énergie la plus basse du peptide PSVKMA sur une machine quantique D-Wave. Récemment, l'équipe de recherche de Babay a étendu les codages de rotation et de diamant pour les modèles 3D et a introduit des améliorations algorithmiques qui réduisent la complexité et la vitesse de mouvement du codage Hamilton [voir Réf. ici ]. Ils ont utilisé un processeur D-Wave 2000Q pour déterminer l'état fondamental de l'Higoline (10 résidus) sur un réseau carré et du tryptophane (8 résidus) sur un réseau cubique, qui sont les plus gros peptides étudiés à ce jour. Ces mises en œuvre expérimentales utilisent une méthode dans laquelle une partie du peptide est fixée. Cela permet d'introduire de gros problèmes dans un ordinateur quantique en raison de la possibilité de recherchele nombre de paramètres du problème étudiés.
Trouver la conformation à énergie la plus basse dans le modèle de réseau est un problème NP difficile [cf. ici et ici ], ce qui signifie que dans les hypothèses standard, il n'y a pas d'algorithme classique de résolution. De plus, on pense actuellement que les ordinateurs quantiques ne peuvent pas offrir une accélération exponentielle pour des problèmes NP-complets et plus complexes [cf. ici ], bien qu'ils puissent offrir les avantages de la mise à l'échelle, connue dans la littérature sous le nom d '"accélération quantique limitée" [cf. ici]. Récemment, le groupe de recherche d'Outerel a appliqué des simulations numériques pour étudier ce fait, concluant qu'il existe des preuves d'une accélération quantique limitée, bien que ce résultat puisse nécessiter des machines adiabatiques utilisant la correction d'erreur ou des simulations quantiques dans des machines polyvalentes tolérantes aux pannes [cf. ici ].
Bien que la plupart de la littérature se soit concentrée sur le modèle de réseau de protéines, un article récent [ ici ] a tenté d'utiliser le recuit quantique pour échantillonner les rotamères dans la fonction énergétique de Rosetta [voir Réf. ici ]. Les auteurs ont utilisé le processeur D-Wave 2000Qpour trouver une mise à l'échelle qui semblait presque constante par rapport au recuit simulé classique. Une approche très similaire a été présentée par le groupe Marchand [voir. here ] pour une sélection de conformères.
conclusions
Un ordinateur quantique peut stocker et manipuler de grandes quantités d'informations et exécuter des algorithmes à un rythme exponentiellement plus rapide que toute technologie informatique classique. Le potentiel des ordinateurs quantiques même petits peut facilement surpasser les meilleurs supercalculateurs existants aujourd'hui, qui au final, dans le cadre de certaines tâches, peuvent avoir un effet transformateur pour la biologie computationnelle, promettant de transférer les problèmes de la catégorie des insolubles à difficiles et complexes à la routine. Les premiers processeurs quantiques capables de résoudre des problèmes utiles devraient apparaître au cours de la prochaine décennie. Par conséquent, comprendre ce que les ordinateurs quantiques peuvent et ne peuvent pas faire est une priorité pour chaque scientifique informatique.
Bien que nous entrions tout juste dans l'ère de l'informatique quantique pratique, nous pouvons déjà voir les contours d'une nouvelle biologie computationnelle quantique pour les décennies à venir. Nous espérons que cette revue suscitera l'intérêt des biologistes computationnels pour des technologies qui pourraient bientôt changer leur domaine d'expérimentation et de recherche. Et les spécialistes de l'informatique quantique, à leur tour, pourront aider les biologistes à développer de manière significative le niveau de biologie computationnelle et de bioinformatique, à partir duquel de nombreux résultats significatifs sont attendus pour toute l'humanité.