problème de Goldbach . Le problème de Goldbach est l'affirmation que tout nombre pair, commençant par 4, peut être représenté comme la somme de deux nombres premiers. Autrement dit, 6 = 3 + 3; 8 = 5 + 3 ... Si je comprends bien, la solution du problème est une preuve ou une réfutation de cette affirmation.
La première chose à faire est d'implémenter une méthode pour vérifier si un nombre est premier. Un nombre premier est un nombre qui n'est divisible que par lui-même et par un.
public static bool IsPrimeNumber(ulong n)
{
var result = true;
if (n > 1)
{
for (ulong i = 2; i < n; i++)
{
if (n % i == 0)
{
result = false;
break;
}
}
}
else
{
result = false;
}
return result;
}
Nous devons maintenant obtenir une collection de tous les nombres premiers jusqu'à ulong.MaxValue = 18446744073709551615 (2 ^ 64-1)
public static IEnumerable<ulong> GetAllPrimeNumbers(ulong maxNumber)
{
List<ulong> primeNumbers = new List<ulong>();
for (ulong i=0; i < maxNumber; i++ )
{
if (IsPrimeNumber(i))
{
primeNumbers.Add(i);
}
}
return primeNumbers;
}
L'intuition suggère qu'il faudra beaucoup de temps pour les calculer, nous allons donc réduire leur nombre à 300000
static void Main(string[] args)
{
Stopwatch stopwatch = new Stopwatch();
stopwatch.Start();
IEnumerable<ulong> primeNumbers = GetAllPrimeNumbers();
checkGoldbach(primeNumbers);
stopwatch.Stop();
Console.WriteLine(" " + stopwatch.Elapsed.TotalSeconds + " ");
foreach(var number in primeNumbers)
{
Console.Write(number + " ");
}
Console.ReadKey();
}

Ensuite, j'ai voulu trouver tous les nombres premiers jusqu'à 2 ^ 64 (il m'a semblé que quelques heures de calculs me suffiraient)
Après deux minutes d'exécution du programme, j'ai décidé de mettre un point d'arrêt et de vérifier quel nombre est vérifié pour la simplicité:
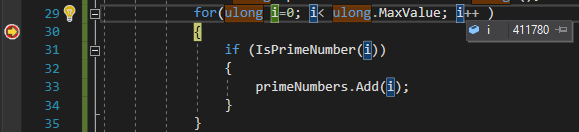
411780 itérations après deux minutes de calculs. J'ai décidé d'optimiser légèrement la méthode de vérification de la simplicité d'un nombre, puisqu'il n'est pas nécessaire de continuer à itérer après la moitié du nombre
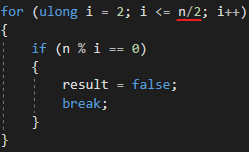
, ainsi le nombre d'itérations nécessaires pour vérifier la simplicité est divisé par deux. Il m'a semblé qu'en 2 minutes le nombre d'itérations devrait doubler

Mais là aussi, je me suis trompé. La productivité n'a pas augmenté de 100%, mais de 22%. Comme je l'ai compris plus tard, cela est dû au fait que la moitié des chèques, comme auparavant, sont éliminés en divisant par 2, un tiers de tous les nombres non éliminés en divisant par 2 sont éliminés en divisant par 3, etc. Sur les 500 154 tests de simplicité, 41 549 nombres premiers ont été trouvés. Autrement dit, l'itération pour
for (ulong i = 2; i <= n/2; i++)
{
if (n % i == 0)
{
result = false;
break;
}
}
exécuté jusqu'à la fin (sans interruption) seulement 41 549 fois. Dans d'autres cas, il a été interrompu plus tôt ...
500154 et pas près de 2 ^ 64, vous devez calculer combien de temps il faudra pour vérifier la simplicité de tous les nombres à 2 ^ 64
Tout d'abord, réduisons le nombre d'itérations de 2 ^ 64 à 30000 et calculons le temps d'exécution de la méthode du chronomètre

pour itérer sur nombres jusqu'à 30000, 1 seconde a été dépensée
maintenant, faisons un tableau avec d'autres valeurs du nombre d'itérations
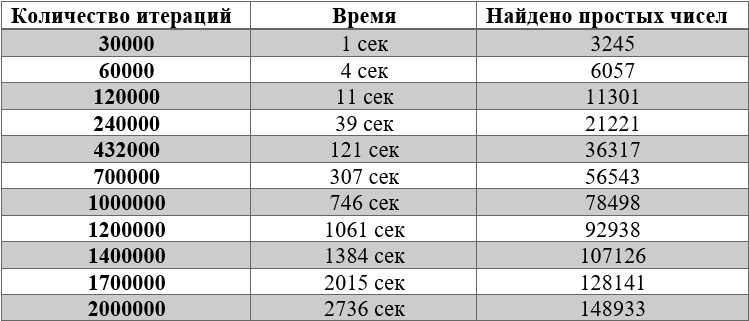
Écrivons le résultat dans Excel, et construisons un graphique à points pour les coordonnées "Nombre d'itérations pour le temps" et "Nombre de nombres premiers par plage"
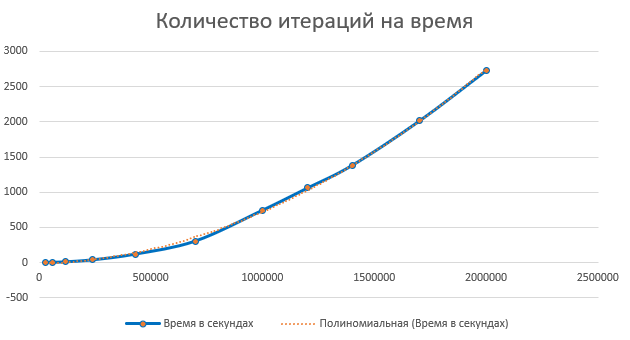
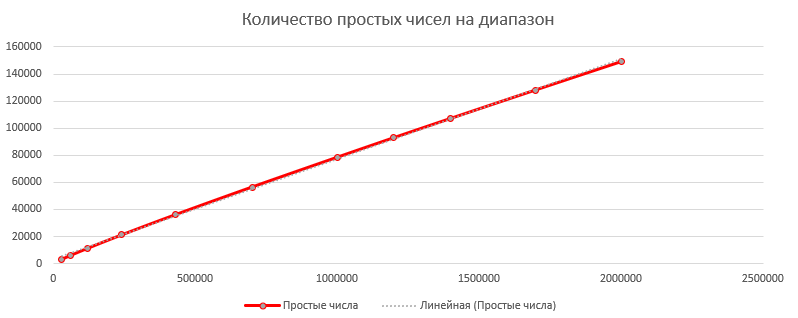
Maintenant, nous pouvons trouver le nombre approximatif de nombres premiers jusqu'à 2 ^ 64, et à peu près combien de temps il faudra pour les trouver tous
Si vous ajoutez une ligne de tendance «linéaire» au graphique «nombres premiers par plage», Excel vous donnera la formule y = 0,074x + 3004 (je ne sais pas à quel point la formule est précise). Cela signifie que le nombre approximatif de nombres premiers jusqu'à ulong.MaxValue = 0,074 * 2 ^ 64 + 3004;
De la même manière, en ajoutant la courbe de tendance "Polynomial" au graphique "Nombre d'itérations dans le temps", on obtient la formule y = 7E-10x2 + 6E-05x. En remplaçant notre nombre 2 ^ 64 au lieu de x, vous pouvez découvrir que pour trouver tous les nombres premiers jusqu'à 2 ^ 64, nous avons besoin d'environ 2,38E + 29 secondes, soit 7553198149564240000000 ans. Ok, je ne peux pas m'attendre à ça.
Essayons de prouver que la conjecture de Goldbach est vraie pour tous les nombres pairs jusqu'à 300 000.
public static void checkGoldbach(IEnumerable<ulong> primeNumbers)
{
ulong numbersCount = 300000;
for (ulong number = 4; number<numbersCount; number+=2)
{
bool isGoldbachResult = false;
foreach(ulong primeNumber1 in primeNumbers)
{
foreach(ulong primeNumber2 in primeNumbers)
{
if(primeNumber1+primeNumber2==number)
{
Console.WriteLine("{0} = {1} + {2}", number, primeNumber1, primeNumber2);
isGoldbachResult = true;
break;
}
if(primeNumber1+primeNumber2>number)
{
break;
}
}
if(isGoldbachResult|| primeNumber1>number)
{
break;
}
}
if(!isGoldbachResult)
{
Console.WriteLine(" " + number + " ");
break;
}
}
}
Si la déclaration de Goldbach n'est pas vraie pour un certain nombre, la méthode arrêtera de calculer à ce nombre.
Après 9 minutes de calculs, on peut dire que l'hypothèse de Goldbach est valable pour des nombres inférieurs à 300 000.
Total
Tout s'est avéré moins simple qu'il me paraissait au début, et je comprends que je ne suis pas du tout près de résoudre le problème.
Très probablement, il me semble qu'il existe de meilleures options pour vérifier un nombre par souci de simplicité. Il est possible que la méthode qui vérifie l'exactitude des nombres pairs pour l'exactitude de la déclaration de Goldbach puisse être mise en œuvre plus rationnellement qu'une simple énumération de nombres premiers, mais je ne veux plus passer autant de temps là-dessus ... La
résolution du problème de Goldbach ne donnera rien à l'humanité. Jusqu'à présent, il a été prouvé que l'hypothèse est vraie pour les nombres jusqu'à 4 * 10 ^ 18, mais à quoi bon le prouver pour tous les nombres? Dans quel but les mathématiciens écrivent-ils des livres sur ce sujet et passent généralement leur temps à résoudre de tels «problèmes»?
Je veux vraiment demander à des personnes bien informées si ma formule de calcul du nombre de nombres premiers par plage a le droit d'exister?
PS
Très probablement, je n'ai pas besoin d'écrire des articles que je connais peu. Je ne m'attendais pas à ce que la communauté réagisse de cette façon. Mais je n’ai pas prétendu que ma décision était la seule correcte. Je suis un amateur dans ce domaine.
Dans quel but ai-je écrit cet article?
J'ai pris le temps de faire des recherches sur cette question et il m'a semblé que certaines personnes pourraient l'aimer. C'était intéressant pour moi car c'est une tâche amusante. Mais pourquoi les mathématiciens perdent-ils leur temps là-dessus? Je ne comprends vraiment pas l’avantage réel de rechercher ces questions spécifiques.
PPS
Après avoir lu les critiques sur l'article, j'ai décidé de tirer des conclusions.
Très probablement, il me semble qu'il existe de meilleures options pour vérifier un nombre par souci de simplicité
Comme suggéré par les utilisateurs dvserg drPourquoi et Pavel_The_Bestça l'est vraiment. Par exemple, en utilisant le tamis d'Eratosthène, une collection de nombres premiers peut être collectée beaucoup plus rapidement. Voici les articles que vous pouvez lire sur ce sujet: Algorithme de vérification de la simplicité en O (log N) , Wikipedia , vous pouvez lire les travaux de Srinivas Ramanujan Iyengor
Ma formule de calcul du nombre de nombres premiers par plage a-t-elle le droit d'exister?
Non
Résoudre le problème de Goldbach ne donnera rien à l'humanité?
Mon opinion que certains problèmes de mathématiques sont inutiles a provoqué une attitude nettement négative de la part de la plupart des utilisateurs. Utilisateursvvadzim Réfrigérateur bromzh Graph-in Réfrigérateur EimKR bfDeveloper et ouiont pu m'en convaincre. Je reprends mes paroles.
Depuis les temps anciens, les mathématiciens recherchent la vérité, et leur recherche conduit souvent à des conséquences bénéfiques pour le progrès. Peut-être que le problème lui-même et sa solution ne donneront rien au monde ici et maintenant, mais ce sont les conclusions tirées lors de la recherche d'une solution qui peuvent être utiles à long terme.