Échange inconditionnel fou

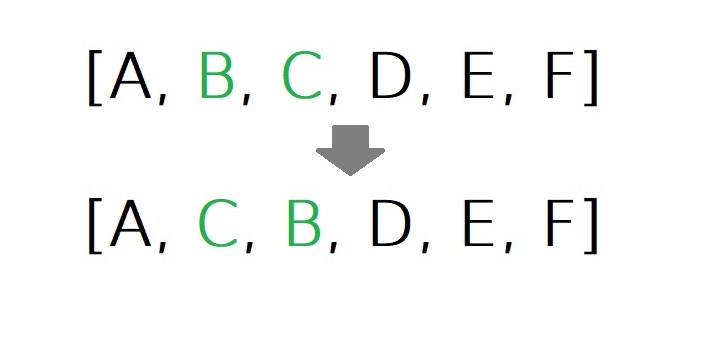
Récemment, je suis tombé sur une tâche de manière immuable d'échanger deux éléments d'un tableau par leurs indices. La tâche est assez simple. Par conséquent, le résoudre de manière raisonnable:

const swap = (arr, ind1, ind2) =>
  arr.map((e, i) => {
    if (i === ind1) return arr[ind2]
    if (i === ind2) return arr[ind1]
    return e
  })

Je voulais le résoudre d'une manière folle. J'ai pensé qu'il serait intéressant de résoudre ce problème:

• Sans opérateurs de comparaison et opérateurs logiques ( &&, ||, ...)
• Sans boucles et ifs et opérateurs ternaires
• Sans utiliser de structures de données supplémentaires
• Pas de casting

Réduire le problème à un plus petit

En effet, cette tâche peut être réduite à une plus petite. Afin de démontrer cela, réécrivons le code ci-dessus de cette manière:

const swap = (arr, ind1, ind2) => {
  return arr.map((elem, i) => {
    const index = i === ind1 ? ind2 : i === ind2 ? ind1 : i

    return arr[index]
  })
}

index, . — ind1, ind2. ind2 ind1. , — — index .

index getSwapIndex(i, ind1, ind2).

const getSwapIndex(i, ind1, ind2) {
  return i === ind1
     ? ind2
     : i === ind2
       ? ind1
       : i
}

const swap = (arr, ind1, ind2) => arr.map((_, i) => arr[getSwapIndex(i, ind1, ind2)])

swap . ,

— . getSwapIndex , . , 1 0. 1 , 0 .

:

type NumberBoolean = 1 | 0

""

const or = (condition1, condition2) => condition1 + condition2 - condition1 * condition2

, 1 0. "" .

or(0, 0) => 0 + 0 - 0 * 0 => 0
or(0, 1) => 0 + 1 - 0 * 1 => 1
or(1, 0) => 1 + 0 - 1 * 0 => 1
or(1, 1) => 1 + 1 - 1 * 1 => 1

, :

const or = (c1, c2) => Math.sign(c1 + c2)

Math.sign(-23) = -1
Math.sign(0) = 0
Math.sign(42) = 1

, , .

const R =  ? R1 : R2
//   -   , R1, R2 -  .
// ,
const R = P * R1 + (1 - P) * R2
//   -       .     === true,  P    1,    === false,  P    0.

P === 0, R = 0 * R1 + (1 - 0) * R2 = R2.

P === 1, R = 1 * R1 + (1 - 1) * R2 = R1.

— .

ternary(c, r1, r2) :

function ternary(p: NumberBoolean, r1: number, r2: number): number {
  return p * r1 + (1 - p) * r2
}

. :

isEqual(a: number, b: number): NumberBoolean

:

const isEqual = (a, b) => {
  return 1 - Math.sign(Math.abs(a - b))
}

Math.abs(-23) = 23
Math.abs(0) = 0
Math.abs(42) = 42

, , . a b — , :

isEqual(a, b)
 => 1 - Math.sign(Math.abs(a - b))
 => 1 - Math.sign(Math.abs(0))
 => 1 - Math.sign(0)
 => 1 - 0
 => 1

, :

isEqual(a, b)
 => 1 - Math.sign(Math.abs(a - b))
 => 1 - Math.sign(Math.abs( ))
 => 1 - Math.sign( ))
 => 1 - 1
 => 0

.

--

getSwapIndex :

const getSwapIndex = (i, ind1, ind2) =>
  ternary(isEqual(i, ind1), ind2, ternary(isEqual(i, ind2), ind1, i))

:

const isEqual = (a, b) => 1 - Math.sign(Math.abs(a - b))

const ternary = (p, r1, r2) => p * r1 + (1 - p) * r2

const getSwapIndex = (i, ind1, ind2) =>
  ternary(isEqual(i, ind1), ind2, ternary(isEqual(i, ind2), ind1, i))

const swap = (arr, ind1, ind2) => arr.map((_, i) => arr[getSwapIndex(i, ind1, ind2)])

, , .

, , :

const getSwapIndex = (i, ind1, ind2) => {
  const shouldSwap = or(isEqual(i, ind1), isEqual(i, ind2))

  return ternary(shouldSwap, ind1 + ind2 - i, i)
}

:

, !