Inventer un vélo ou écrire un perceptron en C ++. Partie 3

Implémentons la formation d'un perceptron multicouche en C ++ en utilisant la méthode de rétropropagation.

Préface

Bonjour à tous!) Avant de passer à la base de cet article, je voudrais dire quelques mots sur les parties précédentes. L'implémentation que j'ai proposée est une parodie de la RAM de l'ordinateur, tk. un vecteur tridimensionnel viole la mémoire avec une abondance de cellules vides, pour lesquelles la mémoire est également réservée. Par conséquent, la méthode est loin d'être la meilleure, mais j'espère qu'elle aidera les programmeurs débutants dans ce domaine à comprendre ce qui est «sous le capot» des réseaux de neurones les plus simples. Cette fois. En décrivant la fonction d'activation dans la première partie, j'ai fait une erreur - la fonction d'activation n'a pas à être limitée dans la plage de valeurs. Tout dépend des objectifs du programmeur. La seule condition est que la fonction doit être définie sur tout l'axe des nombres. C'est deux

introduction

-, . backpropagation — . , !

: habr.com/ru/post/514372

backpropagation — .

, , , .

:

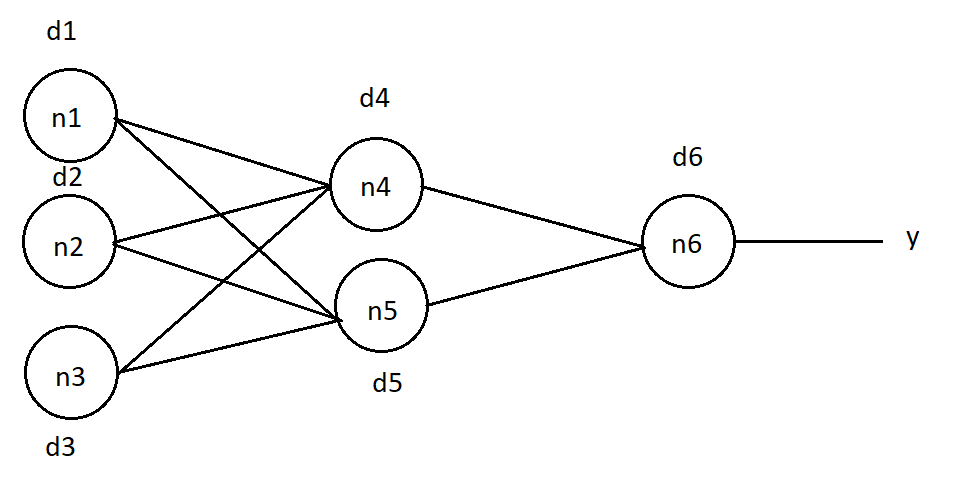
, , . , , . , , . : $$$d j ​ =f(net j ​ )(1−f(net j ​ )) k ∑ ​ d k ​ w kj ​$ (1), j — , , k — , , .. .

, . "O". n6 d6 = (O — y)*( f(in) )*(1 — f(in) ) (2), in —

n6, f(in) — .

(1), . n4 :

d4 = d6 * w46 *( f(in4) ) * (1 — f(in4)), w46 — n4 n6, in4 — n4.

d5 = d6 * w56 *( f(in5) ) * (1 — f(in5)), n5.

d1 = (d4 * w14 + d5 * w15) *( f(in1) ) * (1 — f(in1)), n1, , — .

n2 n3 :

d2 = (d4 * w24 + d5 * w25) *( f(in2) ) * (1 — f(in2))

d3 = (d4 * w34 + d5 * w35) *( f(in3) ) * (1 — f(in3))

, , :

Δw46 = d6 * A * f(in4), w46 — n4 n6 , f(in4) — n4, A — , — , .

Δw56 = d6 * A * f(in5), n5 n6.

:

Δw14 = d4 * A * f(in1)

Δw24 = d4 * A * f(in2)

Δw34 = d4 * A * f(in3)

Δw15 = d4 * A * f(in1)

Δw25 = d4 * A * f(in2)

Δw35 = d4 * A * f(in3)

? . .

void NeuralNet::learnBackpropagation(double* data, double* ans, double acs, double k) {  //data -   , ans -     , k -   , acs-  

, - :

for (uint32_t e = 0; e < k; e++) {
		double* errors = new double[neuronsInLayers[numLayers - 1]]; //      
                // "Do_it"    "Forward"
		Forward(neuronsInLayers[0], data);//    
		getResult(neuronsInLayers[numLayers - 1], errors);//     

:

for (uint16_t n = 0; n < neuronsInLayers[numLayers - 1]; n++) {
			neurons[n][2][numLayers - 1] = (ans[n] - neurons[n][1][numLayers - 1]) * (neurons[n][1][numLayers - 1]) * (1 - neurons[n][1][numLayers - 1]);
		}

, :

for (uint8_t L = numLayers - 2; L > 0; L--) {
			for (uint16_t neu = 0; neu < neuronsInLayers[L]; neu++) {
				for (uint16_t lastN = 0; lastN < neuronsInLayers[L + 1]; lastN++) {
					neurons[neu][2][L] += neurons[lastN][2][L + 1] * weights[neu][lastN][L] * neurons[neu][1][L] * (1 - neurons[neu][1][L]);
					weights[neu][lastN][L] += neurons[neu][1][L] * neurons[lastN][2][L + 1] * acs;
				}
			}
		}

:

void NeuralNet::learnBackpropagation(double* data, double* ans, double acs, double k) {  //k -    acs-  
	for (uint32_t e = 0; e < k; e++) {
		double* errors = new double[neuronsInLayers[numLayers - 1]];
		Forward(neuronsInLayers[0], data);
		getResult(neuronsInLayers[numLayers - 1], errors);
		for (uint16_t n = 0; n < neuronsInLayers[numLayers - 1]; n++) {
			neurons[n][2][numLayers - 1] = (ans[n] - neurons[n][1][numLayers - 1]) * (neurons[n][1][numLayers - 1]) * (1 - neurons[n][1][numLayers - 1]);
		}
		for (uint8_t L = numLayers - 2; L > 0; L--) {
			for (uint16_t neu = 0; neu < neuronsInLayers[L]; neu++) {
				for (uint16_t lastN = 0; lastN < neuronsInLayers[L + 1]; lastN++) {
					neurons[neu][2][L] += neurons[lastN][2][L + 1] * weights[neu][lastN][L] * neurons[neu][1][L] * (1 - neurons[neu][1][L]);
					weights[neu][lastN][L] += neurons[neu][1][L] * neurons[lastN][2][L + 1] * acs;
				}
			}
		}
	}
}

. :

#include <stdio.h>
#include "neuro.h"
int main()
{
    
    uint16_t neurons[3] = {16, 32, 10}; //        , -       
/*        ""  
        
*/
    NeuralNet net(3, neurons);
    double teach[4 * 4] = {//  ""  "4"  , - : 4*4 = 16
        1,0,1,0,
        1,1,1,0,
        0,0,1,0,
        0,0,1,0,
    };
    double test[4 * 4] = {//  "4",  -
        1,0,0,1,
        1,1,1,1,
        0,0,0,1,
        0,0,0,1,
    };
    double ans[10] = {0, 0, 0, 0, 1, 0, 0, 0, 0, 0,};//       , "1"    ,       "4"
    double output[10] = { 0 };//      
    net.Forward(4*4, teach); //    
    net.getResult(10, output); 
    for (uint8_t i = 0; i < 10; i++) printf("%d: %f \n", i, output[i]*100); //  
    net.learnBackpropagation(teach, ans, 0.50, 1000); //    "test",  : 0.5
    printf("\n");
    net.Forward(4 * 4, test);//     
    net.getResult(10, output);
    for (uint8_t i = 0; i < 10; i++) printf("%d: %f \n", i, output[i]*100);
    return 0;
}

:

( ), , 0 9. . , «4»

, , - , . . . , , .

...

. , .

Merci pour l'attention portée à cet article et pour les commentaires sur la publication précédente. Je dupliquerai le lien vers les fichiers de la bibliothèque.

Laissez vos commentaires, suggestions. À plus tard!